Part 3: Calibration & Imaging of 3C345
This is the CASA v5 version of this tutorial! If you don't mean to be here, got back to the Unit 4 workshop page to get the CASA v6 tutorials.
This section expects that you have completed part 1 and 2 of the EVN continuum tutorial. You should now know the basics of VLBI calibration and the secondary calibration including self-calibration and imaging. In this section, we shall focus on our second pair of phase calibrator, target pairs in this observation.
While in the last section, we simply inputted parameters into CASA tasks, this section expects that you can generate a script on your own with some help and pointers. It is designed so that you can become proficient in applying these techniques to other data sets and at the end we shall explore something new, namely weighting and analysing images.
Table of contents
- Data and supporting material
- How to approach this workshop
- Remove bad data
- Refining phase calibrator calibration
- Image phase calibrator
- Find phase calibration solution interval
- Correct residual delay & phase errors
- Apply phase calibration and re-image
- Generate amplitude solutions
- Apply corrections to phase cal
- Apply solutions to target and split
- Self-calibration on target
- Imaging the target
1. Data and supporting material
For this section, you will need the scripts contained in EVN_continuum_pt3_scripts.tar.gz (download link on the homepage) and the $uv$ data J1640+3946_3C345.ms from part 1. Put these two files into a different folder so that you can distinguish between parts 1, 2 and 3 of this tutorial and un-tar the scripts. YOu should have the following in your folder:
J1640+3946_3C345.ms - partially calibrated $uv$ data from part 1. Note that if you find weird results, please untar NME_3C345_all.py.tar.gz- complete calibration script in case you get stuck.NME_3C345_skeleton.py- calibration script we will be inputting to.flag_TarPh.flagcmd.tar.gz- complete flagging commands to remove residual bad data (only use if stuck or are low on time!)flag_template.flagcmd- template flagging commands for removing bad data
J1640+3946_3C345.ms.tar.gz data set and use that uv data.
2. How to approach this workshop
This workshop is a little different to the previous parts and aims to help you generate a script from scratch. We shall begin by helping out with the task names, however, later on this is completely down to you (with some useful hints of course!).
To begin:
- Open
NME_3C345_skeleton.pyand you will see that the preamble is similar to the script from part 2
The first thing we want to do is to set some variables in the script to make it easier if you want to use the same script to reduce some other, similar data.
- Look at lines 26-30 in the skeleton script and use the task
listobstask to set the paramters.
target='**' # target source
phscal='**' # this is the phase calibrator
antref='**' # refant as origin of phase
flag_table='**' ## wait until step 2 to set this!
parallel=False ## Only works for linux atm (need to init with mpicasa -n <cores> casa)
You should either have remembered (from part 1) or identified that the phase calibrator is J1640+3946 and the target is 3C345. One thing you may have seen from listobs is that there's a long scan of the target at the start of the observation. This is non-normal but we will recover this data.
- With these parameters set, look at the title of the steps and try to get a feel for the various steps we are going to do and start to think about the CASA tasks we shall use to achieve it
If you are ready, then we shall begin to fill in the script.
3. Remove bad data
3A. Inspect data
As you may remember, one of the best things to do is to know your data. That means inspect it thoroughly and continually during the calibration process. While in part 1, we removed the majority of bad data, the initial fringe fitting calibration has revealed some other low-lying bad data. First thing we want to do is to identify the bad data and remove it.
- Look at step 1 in the skeleton script and the hints included. To identify bad data, use
plotmsto iterate across the various baselines to see if you find bad data (an example of some bad data is shown below) - Add the
plotmscommands into step 1 of your code
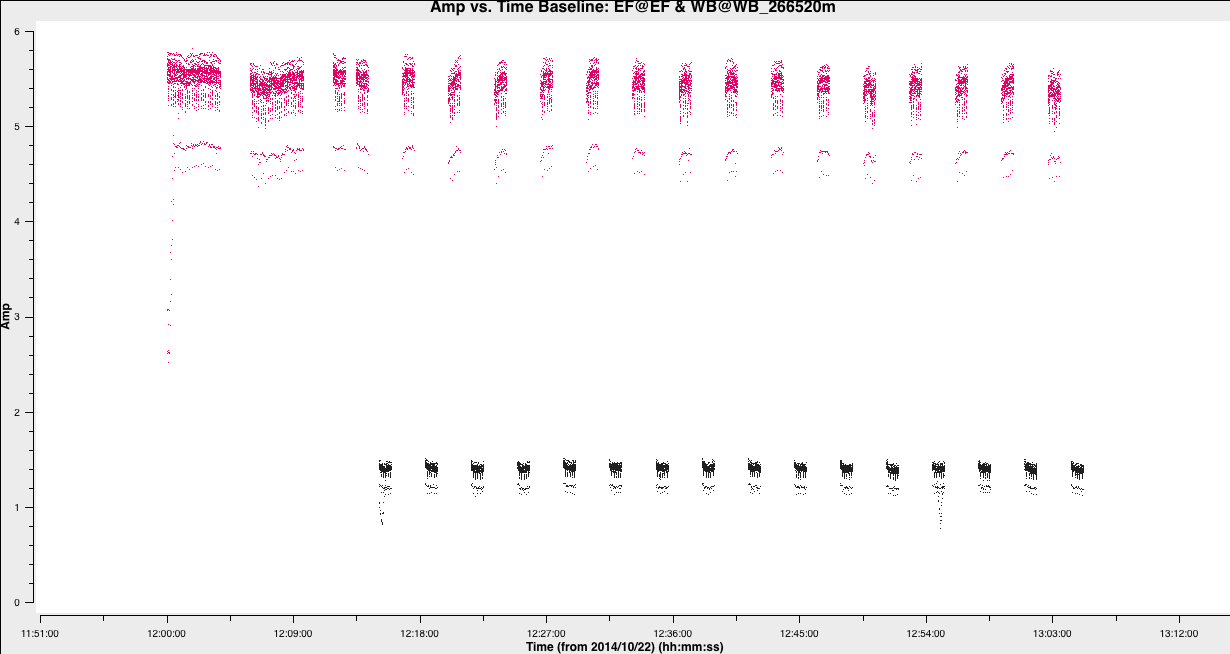
Rather than using the interactive flagging tool available in plotms, we want to write a flag file so that we can perform the same flagging should we need to restart from the beginning (sometimes data can be lost or corrupted). Let's try to fill this.
- Open the file
flag_template.flagcmdusing your favorite text editor - Go through all the baselines again in
plotmsand use the search and locate function to identify the spw, field, baseline and timerange corresponding to the bad data. Note these down in the flag file. - Remember to check whether this is just constrained to one baseline or the entire antenna. This will reduce the number of flag commands you have to write in the file
If you get stuck, or want to compare to the complete flag list, untar the flag_TarPh.flagcmd.tar.gz file and take a look. Note that if you are low on time, you can use this file to do the flagging for you as generating the flagging file can be time consuming.
Once you are happy with your flag file, let's move onto step 2 where we shall apply the flags.
3B. Flag bad data
In this step, we want to use our flagging commands to remove all the bad data and then inspect that all the bad data has been removed.
- Look at step 2 and add in the parameters to the two tasks which should flag and then plot the cleaned data. Remember to make sure that the flags are backed up in case the flagging goes awry. Use the
flag_tableparameter to set the flagging table you have made. - If you are happy, execute step 2. If you find errors, check the syntax of your flag file and indenting in your script.
You should find that your data is clean. In the plot below we illustrate this by plotting the amplitude vs time for all of the baselines to the reference antenna. You can see that nearly all the bad data has gone and we just have some mis-scaled amplitudes.
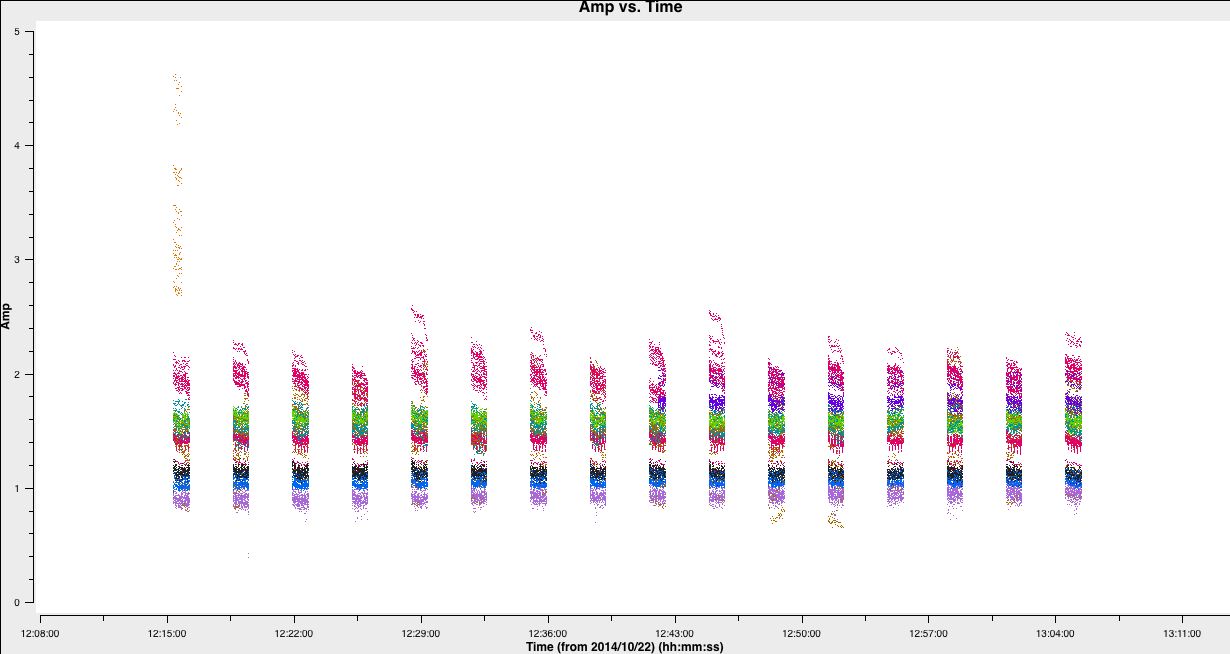
If you find that you find that too much/too little data has been flagged, you should reset the flags using the restore function of the flagdata task and then add/remove commands to your flag file and re-run step 2.
4. Refining phase calibrator calibration
If you remember from part 1, we have some issues with the delays on Shenshen. This was due to the instrumental delay jumps between scans. In part 2, we fixed this for the other phase calibrator-target pair by solving for delays and phase without combining the spectral windows. We will do the same here simply because we have sufficient flux in our phase calibrator to do this ($\sim 1.4\,\mathrm{Jy\,beam^{-1}$). Often VLBI phase calibrators need to have all spws combined in order to get enough S/N to derive accurate time-dependent delays, rates and phases.
Now the holding hands part has finished. From now on, no task names nor parameters shall be supplied, and so calibration is down to you. However, not all is lost as the calibration steps to conduct are almost identical as in part 2 of this workshop.
Good luck and let's continue.
4A. Image phase calibrator
The first step we want to do is to image the phase calibrator to ensure that it is not resolved and, if so, to provide a model to refine the delay and phase calibration. Remember that we also want to FT transform the model into the data for calibration purposes.
- Look at step 3, and input the two tasks that will image the phase calibrator and then Fourier Transform the model generated into the measurement set
- We want to track the S/N so to track improvements with each calibration stage. The appropriate code is provided so you just need to set the boxes again so that the peak and rms values can be derived automatically
You should find that there are non-Gaussian noise i.e. stripes around the phase calibrator, which is tell-tale signs of mis-calibration. I managed to get a peak brightness, $S_p$, of $1.448\,\mathrm{Jy\,beam^{-1}}$, a rms of $0.025\,\mathrm{Jy\,beam^{-1}}$ and so a $\mathrm{S/N}=58$. You should have values near this.
4B. Find phase calibration solution interval
The next step we need to do is to derive our phase calibration solution interval. Our phase calibrator is bright so we should be able to track this on each baseline.
- In step 4, input the commands to plot the phase against time for the baselines to the reference antenna (should be EF!). We want to iterate over the baselines so only one baseline should be plotted at once. In addition, make sure that the plot is colored by field so that we can discern between the target and phase cal easily.
- Execute the step and uou should get a plot similar to the one below!
- Iterate over the baselines and notice how all the phases are misaligned in the SH baselines. We will fix this next steps
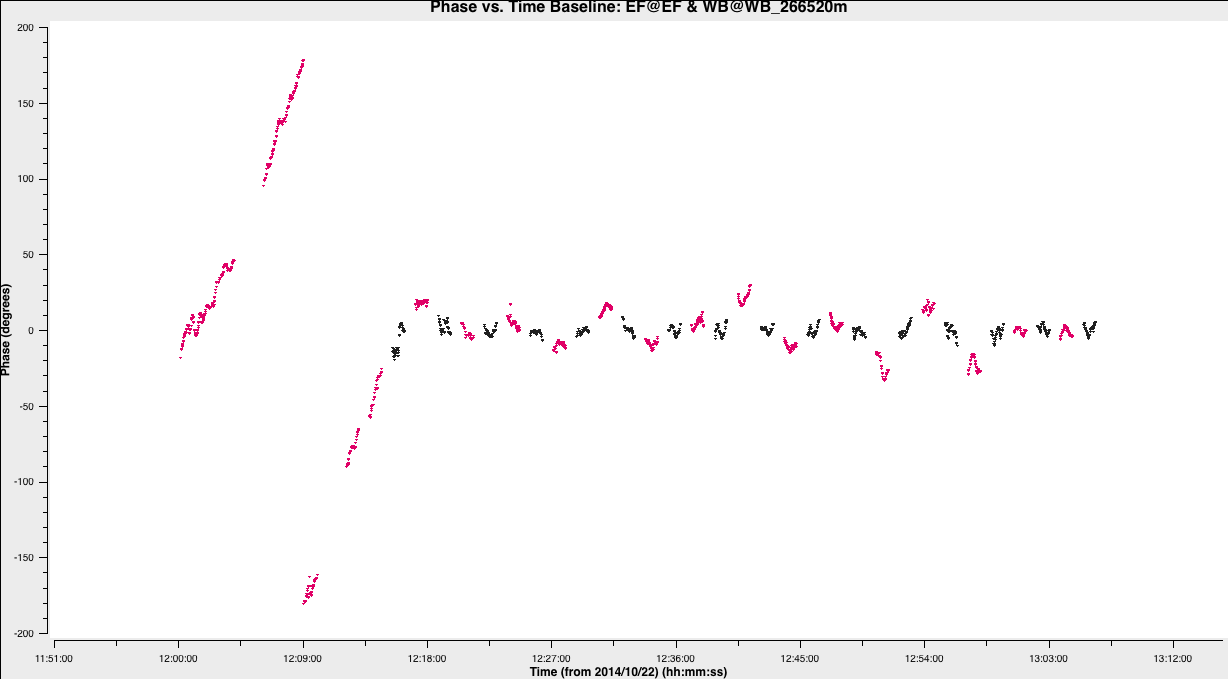
In particular, there are two factors about the above plot which is non-standard for radio interferometric observations, but you should bear in mind. This is a good exercise in getting to know your data. These are:
- We can also track the target phases per baseline. Often your target is not bright enough to do this and will look more like uncalibrated noise. Note that the phases largely track the phase calibrator phases because we have transferred our fringe-fitting solutions to the target in part 1 of this tutorial. However, you can see that they do deviate more that the phase calibrator scans. This is because the phase solutions on the phase calibrator is only approximately correct for the target field. These fluctuations are corrected using self-calibration on the target as we did in part 2 for the other pair of sources
- The target has some long scans at the start of the observation whose phases cannot be constrained as there's no phase calibrator scans surrounding it. This is non-normal as, if the target was not bright enough to perform self-calibration, we wouldn't be able to self-calibrate these scans and would have to flag them (otherwise we'd just be adding noisy uncalibrated data which causes imaging errors). We shall show the effect of including this uncalibrated data later.
Anyways, let's get back to it. If you remember from earlier we want to track the phases within a scan, so we want at least two data points per scan. Find what solution interval gives you that a remember it for the next section. Note that for delays we want to maximize S/N so a per scan solution interval should be sufficient!
4C. Correct residual delay & phase errors
With our solution intervals in mind, we want to derive the refined delay and phase solutions for our data.
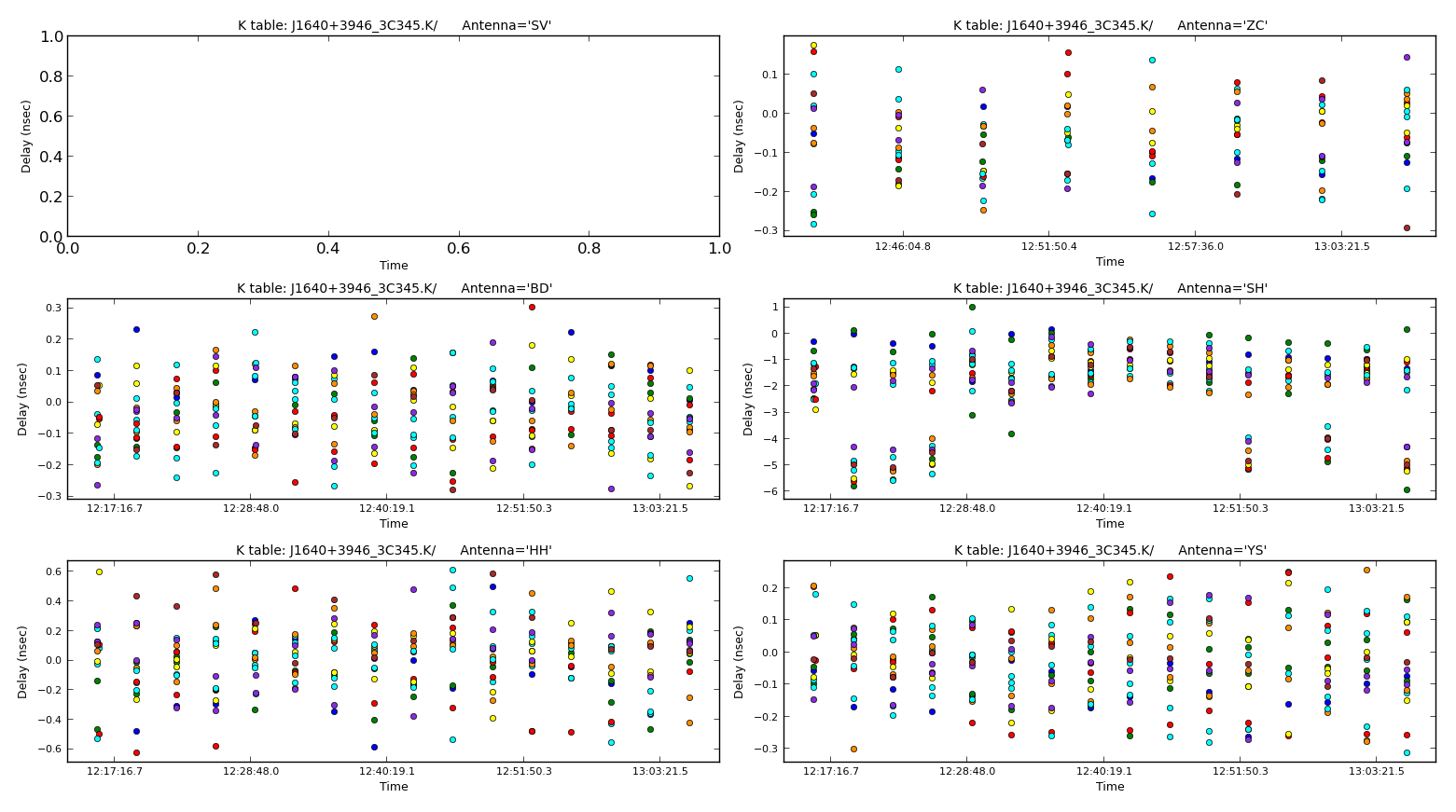
- In step 5, type in the four tasks that will do the following. 1) Produce delay calibration solutions per spw using a solution interval that maximises the S/N per scan. 2) Produces phase calibration solutions per spw using a solution interval that can track phases within the scan. And 3) plot both of these calibration tables, iterating over the antennas
- Once you are happy execute step 5 and you should get plots similar to those shown below
For delays:
And for phases (note a 20s solution interval was used):
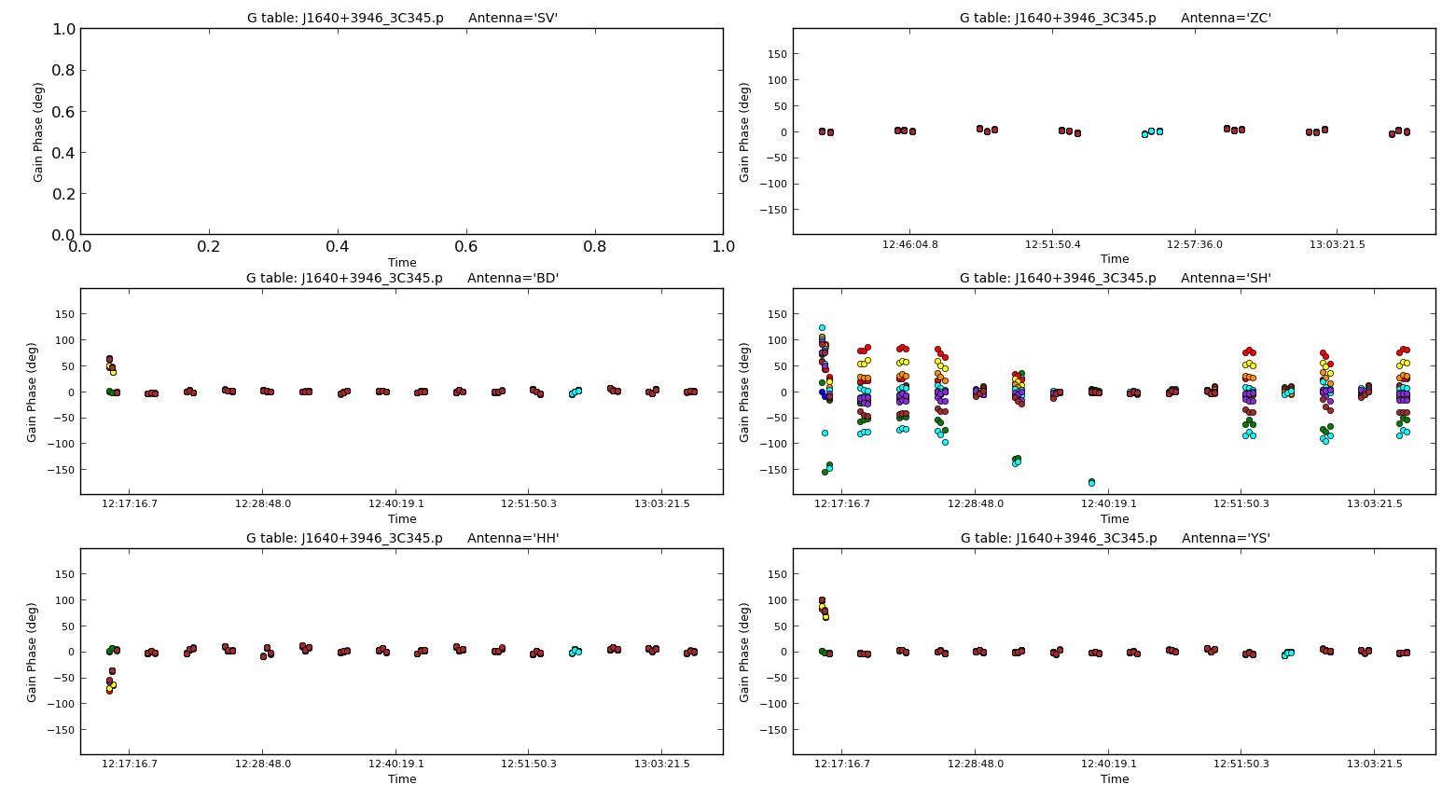
You should be able to see that most solutions are small as we have already derived good solutions using fringe fitting. However, the corrections on Sh is significant and should now be sufficient in calibrating this antenna.
4D. Apply phase calibration and re-image
The next step is to apply these solutions and re-image the phase calibrator again.
- In step 6, input the four tasks that will do the following:
- Apply the solutions we just derived to the phase calibrator only. We want to ensure all calibration is good before we transfer to the target.
- Re-image the phase calibrator again (you can use similar parameters as before, just ensure the imagename matches the calibration steps so you can track it)
- FT the model into the phase calibrator visibilities
- Determine the S/N by extracting the peak flux and r.m.s. from the image produced
- Once you are happy then execute step 6
I managed to get a modest improvement with $S_p = 1.517\,\mathrm{Jy\,beam^{-1}}$, $\sigma= 0.024\,\mathrm{Jy\,beam^{-1}}$ and so a $\mathrm{S/N}=64$
4E. Generate amplitude solutions
Next we want to derive amplitude solutions as we saw some mis-scaled amplitudes in the flagging step. This should align all of our antennas and should dramatically increase our S/N.
- In step 7, input the task that will produce amplitude solutions. We want to maximise the S/N for amplitudes (and they normally vary slower vs time) so you want to have a longer solution interval. Normally a per scan interval will be ok. Remember we have already set the fluxscaling so we want the solutions to be normalised as to not change this. Also, remember that we need to apply all previous calibration of the fly in this task!
- Also input the task to plot these solutions per antenna to ensure that the solutions make sense.
You should find solutions similar to those shown below:
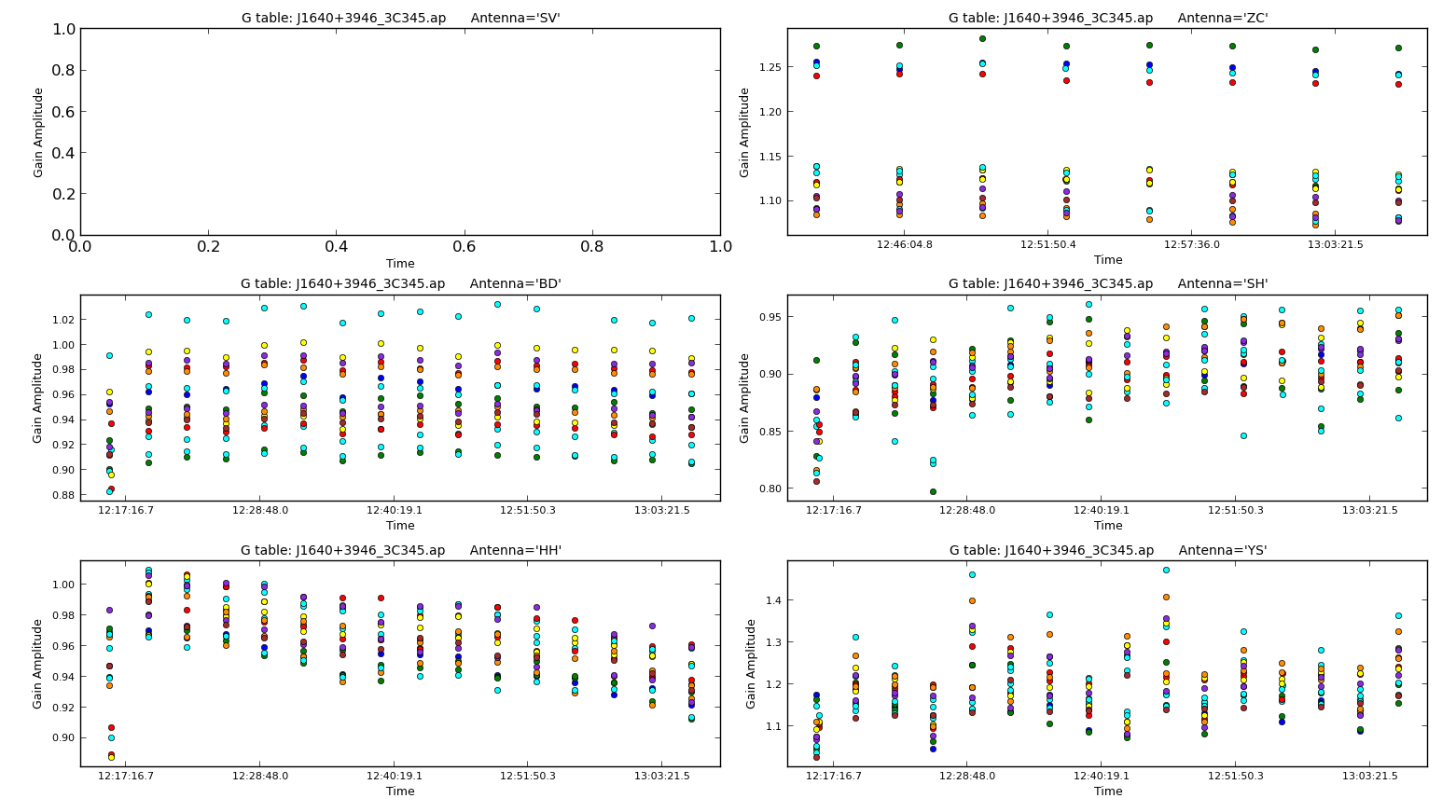
Some antennas have some re-scaling applied but most solutions are close to unity. The first scan has some rescaling applied and it also had large corrections in the phase solutions too. Let's check the calibration by imaging again!
4F. Apply corrections to phase cal
Next we need to apply the amplitude solutions to the phase calibration and assess these solutions by imaging the phase calibrator for a final time.
- In step 8, input the tasks which will apply all of the calibration derived so far to the phase calibrator. Remember CASA calibration always applied corrections to the original DATA column not the CORRECTED data so all calibration needs to be applied again.
- In this step, image the phase calibrator again and assess the improvements by calculating the S/N as before.
- A total of 3 different tasks should be used to do this. Note we don't need to FT the model into the visibilities anymore as calibration on the phase calibrator is complete
The image made should show a dramatic increase in the S/N and the non-Gaussian ripples should have reduced in amplitude dramatically. I managed to get $S_p = 1.532\,\mathrm{Jy\,beam^{-1}}$, $\sigma= 1.94\,\mathrm{mJy\,beam^{-1}}$ and so a $\mathrm{S/N}=791$. You should get close to this (500+) or higher S/N!
4G. Apply solutions to target and split
With us being happy with the calibration refinements we made, we should now apply these to our target source.
- In step 9, type the command that will apply the calibration solutions to the target source. Remember that we want to linearly interpolate these onto the target as the scans are interleaved between the phase calibrator scans
- Input the command which will then split out the corrected target data into a separate measurement set named
3C345.ms. This will now be our new data set for the self-calibration of the target field
5. Self-calibration on target
In the next steps we will concentrate solely on the target source. Our phase calibrator should have given us the approximately correct phase vs time and frequency. However, we want to refine this and take out the phase differences induced by the atmospheric differences between the phase calibrator field and the target. We shall employ self calibration to do this.
5A. First image of target
The first step we want to do for self-calibration is to make a good model of our source.
- In step 10, input the commands to generate an image of the target source. Remember that we should be working from the new measurement set that we have just generated.
- Input the commands to get the S/N ratio
Now, there's something we should remember from before, and that's the long scan of the target that remained uncalibrated after the phase referencing. By including these scans, you'll find that your S/N of the initial target is $\leq10$ (I got $S_p = 1.658\,\mathrm{Jy\,beam^{-1}}$, $\sigma = 0.193\,\mathrm{Jy\,beam^{-1}}$ and a $\mathrm{S/N=9}$). Let's see what happens when we exclude these data.
- In step 10, set the
timerangeparameter in the imaging task to exclude the uncalibrated portions of the data - Execute step 10 (but remember to either change the imagename or delete the first set of images made before otherwise it'll crash!)
By excluding these scans, you should get a dramatic increase in the S/N. I managed to get $S_p = 2.578\,\mathrm{Jy\,beam^{-1}}$, $\sigma = 0.038\,\mathrm{Jy\,beam^{-1}}$ and a $\mathrm{S/N=67}$. The plot below illustrates this. You can see the various amplitude and phase errors on the left panel (deep troughs) where the uncalibrated data is included while the right panel is much more cleaner and has a higher peak flux density. Note that the colorscale is identical for both plots.
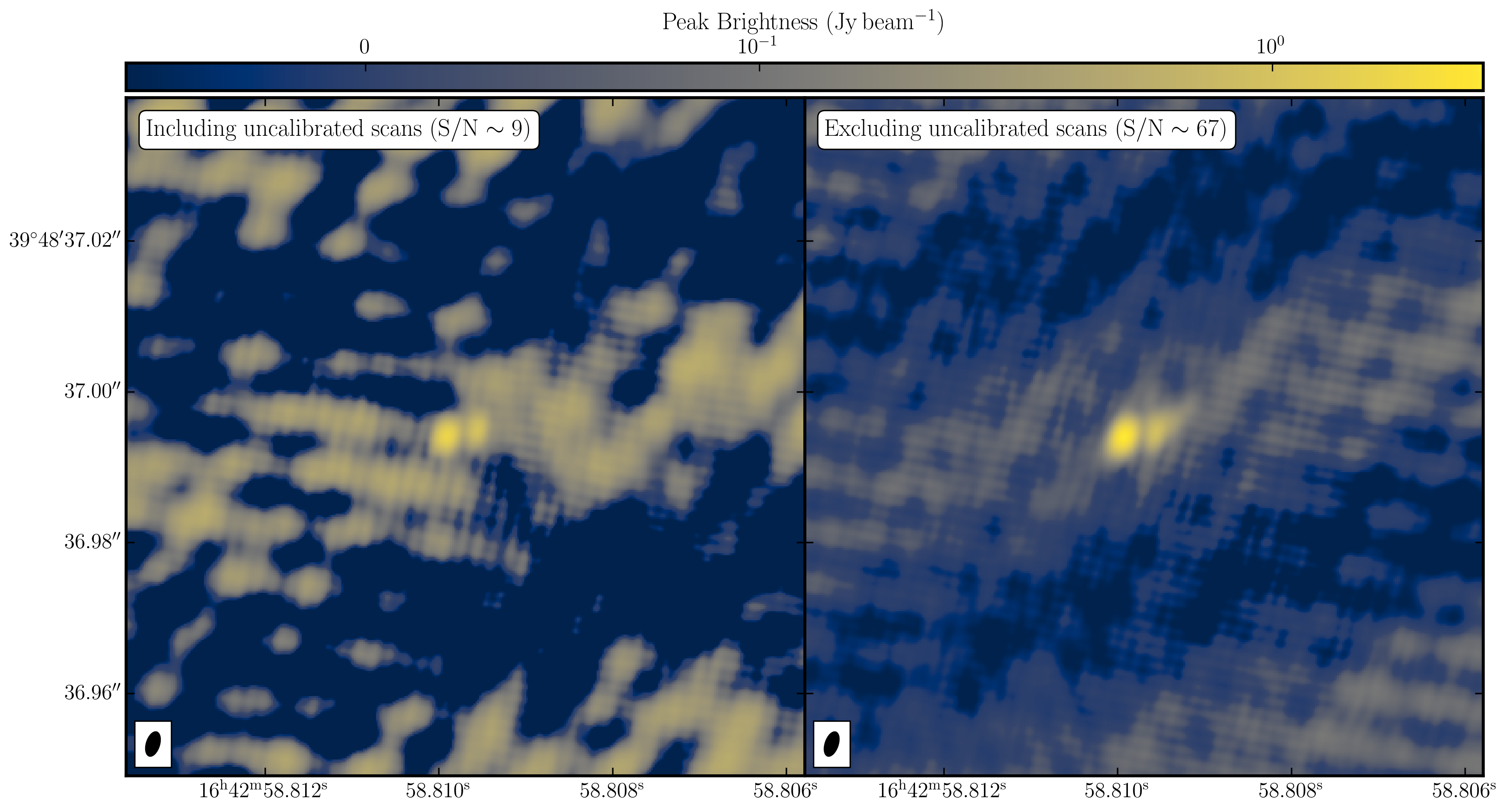
This is a prime example of understanding your data and highlights how keeping 'bad' or uncalibrated data can adversely affect your radio images. This is why understanding your data, planning a calibration strategy and removing RFI can drastically improve your calibration of radio interferometric data.
In this case we have to decide what are we going to do with these uncalibrated scans?. We could: 1) flag the data or 2) try to calibrate it. Flagging the data would be simple, however, we would lose sensitivity as a result. Instead, we can try using the model derived using the calibrated scans to calibrate the uncalibrated long scans. The S/N of >50 should be sufficient to do this!
5B. Self-calibration phase
Let's try to remove the atmospheric phase fluctuations on the target field and calibrate the first few scans. Again, we shall need to think about a suitable solution interval to track the phase within a scan!
- In step 11, type in the task to derive phase only calibration solutions and plot these solutions for each antenna. Remember that to track phases within scans we want at least 2 points per scan so adjust your solution interval for this
- If you are happy, execute step 11
If everything went to plan (and the correct model is FT into the data i.e. without the uncalibrated scans), you should get phase solutions similar to those below:
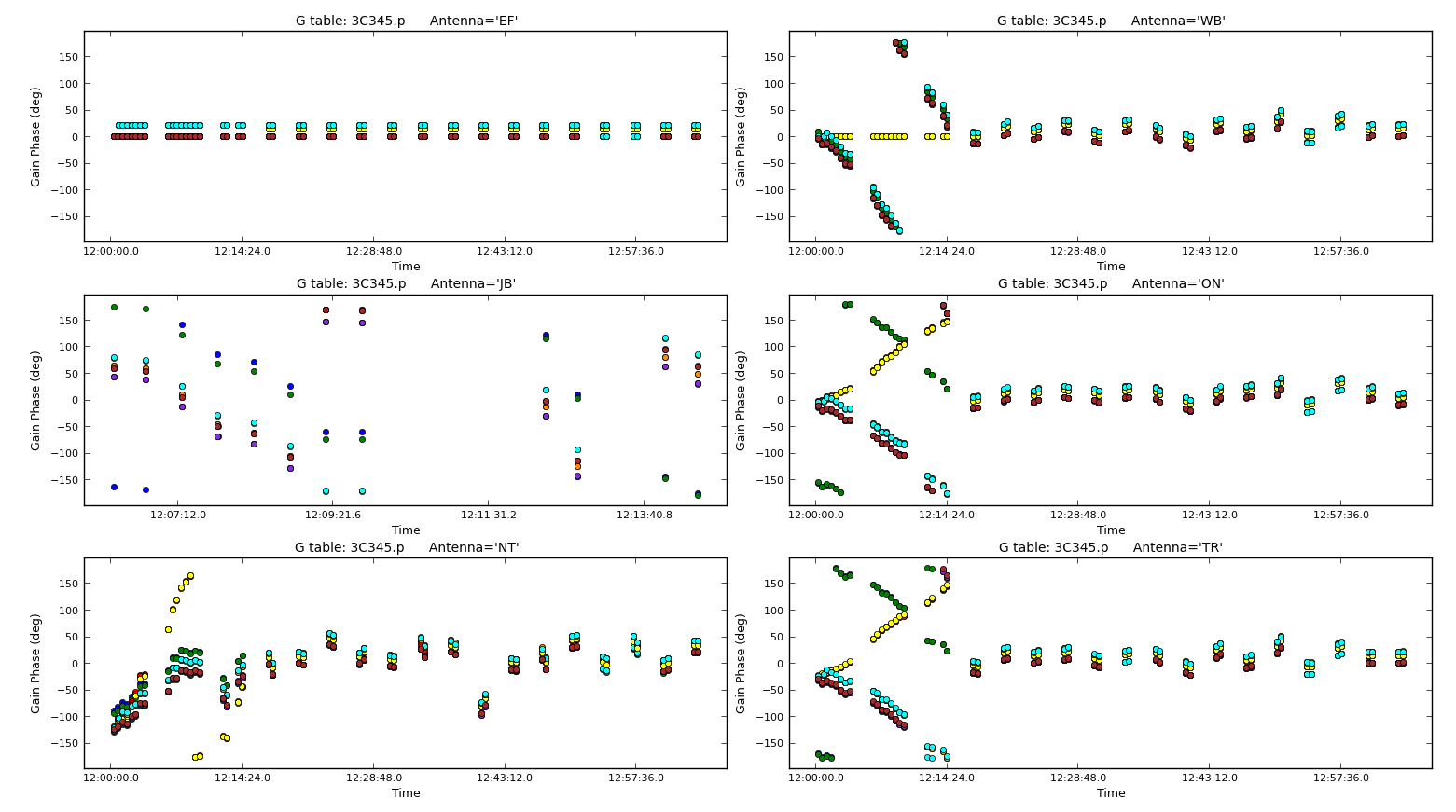
Hooray, our calibration strategy looks to have worked as the initial uncalibrated scans have phase corrections which are broadly similar to the phase vs time plots we made in part 4.B. of this tutorial. For the rest of the scans, the corrections are small ($\sim30^{\circ}$), but should have corrected for the atmospheric differences between target and phase calibrator.
- As we are happy, move onto step 12. Now we have solutions, we need to apply these to the data to generate the CORRECTED data column. Interpolation type is important here!
- Also in this step, we want to image the target again and track the improvements in S/N we got from our calibration
- In addition, this new model should be FT'ed into the measurement set to update the model column for further self-calibration
- You'll need 5 tasks for this part and once you're happy with your entries execute step 12
I managed to get a slight increase in S/N to 92 ($S_p = 2.771\,\mathrm{Jy\,beam^{-1}}$, $\sigma = 0.030\,\mathrm{Jy\,beam^{-1}}$). This is primarily due to the peak flux density increasing. The phases determine where the flux density is therefore, mis-calibrated phases move a proportion of flux from the source into the noise. Re-calibrating this therefore can increase the peak flux density, while simultaneously reducing the noise.
5C. Self-calibration amplitude
In the previous section, we performed a self-calibration cycle to correct for phases. The next task is to now correct for amplitude errors. The majority of these errors, which are caused by the antennas, should have been corrected by the amplitude calibration on the phase calibrator. However, there can be some scan to scan differences which can be corrected.
- In step 13, type in the task to derive amplitude and phase calibration solutions and plot these solutions for each antenna. Remember for amplitudes one point per scan if often sufficient as we want to maximise S/N
- If you are happy, execute step 13
You should find some slight re-adjustments especially on the first, previously uncalibrated, scan which should look similar to the plot below:
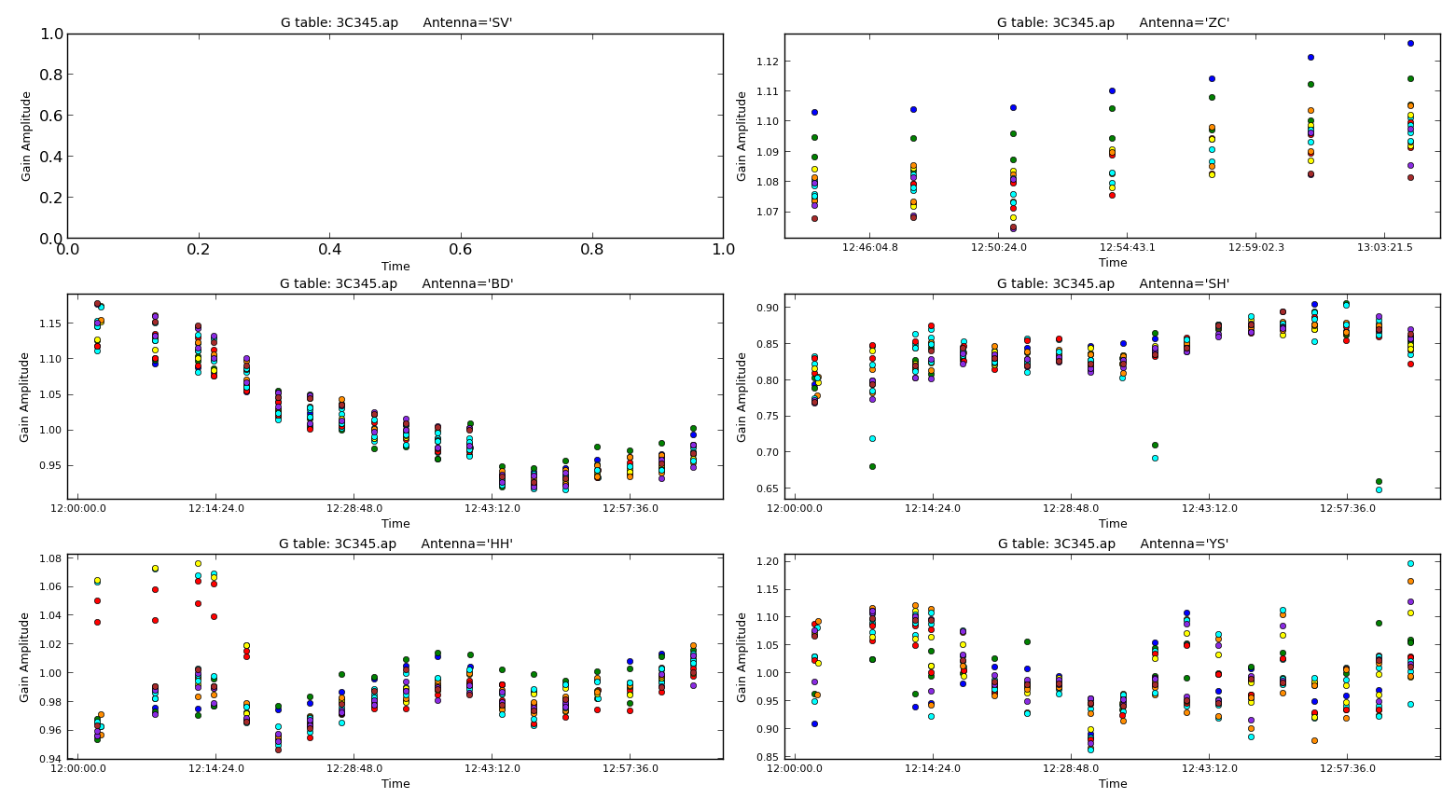
Next, we should take a look to see whether the amplitude self-calibration has improved our target image
- In step 14, add the tasks that will 1) apply the calibration solutions, 2) image the calibrated data and 3) track the S/N increase. This should comprise of 3 tasks.
- Execute step 14
You should find a vast improvement in the S/N to 657 ($S_p = 2.702\,\mathrm{Jy\,beam^{-1}}$, $\sigma = 4.111\,\mathrm{Jy\,beam^{-1}}$). This is mainly due to the initial scan now being fully calibrated.
Next we want to image the data in different ways in order to investigate the structure of the source.
For bookkeeping purposes, we should split the fully calibrated data out. This has already been provided in step 15 so:
- Execute step 15 to produce
3C345_calibrated.ms
6. Imaging the target
6A. Optimising sensitivity via reweighing
As we have a heterogeneous array, the optimal weights when imaging should take into account the sensitivities of the baselines i.e. more sensitive baselines = higher weights. Calibration can do this, but the best way is to look at the noise on each baseline to estimate the sensitivity. More sensitive baselines will have less noise.
Luckily CASA has a task that can do this called statwt. This looks at the rms / std on each baseline and re-adjusts the weights based upon this. This task has to be done after calibration as mis-calibrated data or RFI can adversely affect the estimation of the weights.
- Look at step 16. The
statwtcommand has been inputted for you. We shall be using default parameters and will estimate the weights from the DATA column as we are now using the split dataset - We want to look at the weights assigned so input the parameters into
plotmswhich will plot the weight vs uv wave for all baselines to Onsala. This should create a plot like below (which is colored by baseline)
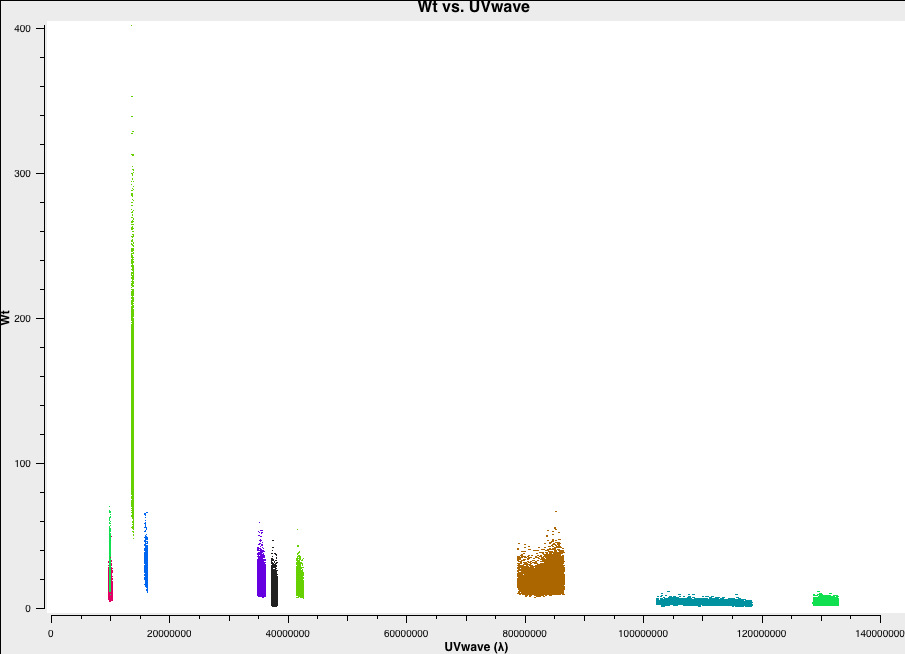
As you can see, the highest weight is given to the baselines with the largest telescope (i.e. Effelsberg). This means that these baselines will be expressed more when imaging resulting in optimal sensitivity.
6B.Experimenting with weightings
For the final part of this workshop, we shall experiment with changing the weighting when imaging. From the lectures, you may know that the weighting you apply to the data when imaging determines what spatial scales are expressed when imaging. This is important as you can often see more structure when changing the weighting.
- Look at step 17 and input the parameters into
tcleanwhich will generate an three images with natural, uniform and robust (0.5) weightings. - You may need to decrease the cell size for the uniform weighting
- Clean the images and then look at them in the viewer
The naturally weighted image should provide the best sensitivity, but poorer resolution. This is because the more sensitive, but shorter, central European baselines dominate the weights hence you get poorer resolution.
In contrast, the uniformly weighted image increases the weighting of the longer baselines which causes the resolution to improve and more complex structure of the source appears. In particular the left blob, now has two components. However, this increase in resolution comes at a cost of worse sensitivity. This is because the sensitive European baselines are down-weighted
The robustly weighted image provides a compromise between the uniformly and naturally weighted images providing intermediate resolutions and sensitivities. In the plot below we have overlaid the three images using python. The background image is the naturally weighted image and the contours are the re-weighted images. You can clearly see the differences between the resolutions (bottom left ellipses) and structure of the source.
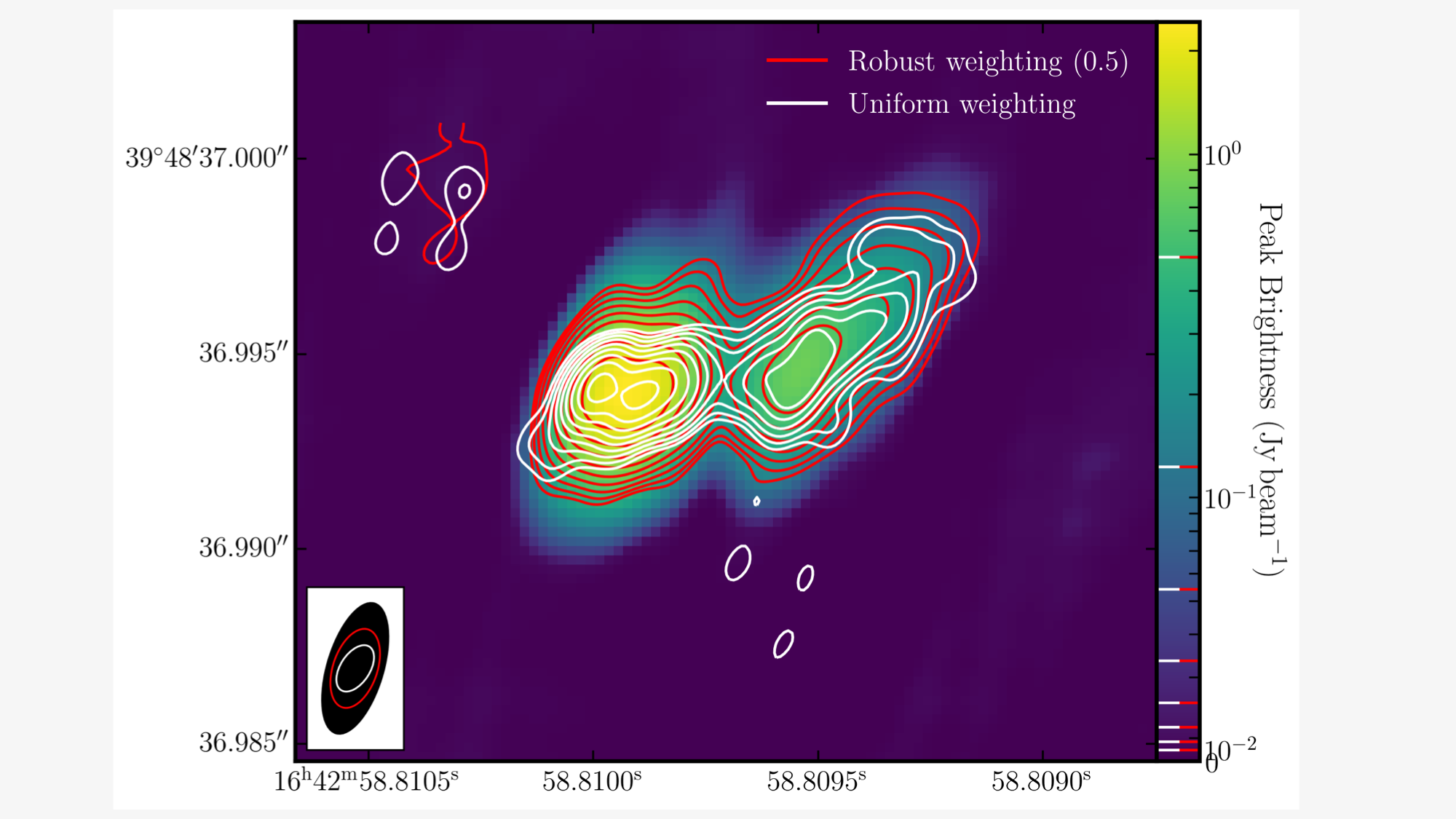
This concludes the EVN continuum tutorial and should have hopefully provided with you with an insight into how to reduce VLBI data. If you would like to do more, check out the spectral line and 3C277 e-MERLIN tutorials. If you have comments, find issues, or need extra help, please use the form below and we will email you back asap.
