2.3 The Early History of the Universe

The CMB gives us our most direct insight into the early stages of the expansion of the Universe. In this section I will summarise our current picture of the Big Bang; later we will see how CMB science has built up, challenged, and confirmed this picture.

2.3.1 The primordial heat bath

In Section 1.3.3 we saw that in the very early Universe radiation density is the only important term in the Friedman equation, which then reads

H² = $${8 \pi G \over 3}$$$$\rho_{r}^{}$$.

Remembering that $\rho_{r}^{}$ $\propto$ R^-4, we can write the Hubble parameter in terms of the age of the universe as

H = $${1 \over t_H}$$ = $${1 \over 2 t}$$

So the Friedman equation says

$$\rho_{r}^{}$$ = $${3 \over 32 \pi G}$$t^-2

Remarkably, the Friedman equation alone tells us the radiation density at any time in the early Universe; there are no free parameters that have to be measured. The theory of the Big Bang, in essence, simply follows through the logical consequence of this equation.

Although photons are very important in the early universe, the density of ordinary matter would of course also have been very high, so that at early enough times the universe must have been optically thick. Photons would travel a very small distance before being absorbed by matter particles, but these collisions, and collisions between matter particles, would continually emit new photons. In a very short time this would lead to complete thermal equilibrium from almost any starting point; that is, both matter and radiation would have thermal energy spectra (black body in the case of photons) characterised by a single temperature. As we have seen, black body radiation has energy density

$$\rho_{\rm photon}^{}$$c² = u_photon = aT⁴

The Friedman equation shows that the temperature steadily falls with time:

T $$\propto$$ t^-1/2 $$\propto$$ R^-1

As R/R₀ = (1 + z) this is just the equation for a redshifted black body we derived in Section 2.1.3, but there we assumed that photons were neither emitted nor absorbed as the universe expands; now we see that absorption and emission have no net effect provided the universe remains in thermal equilibrium^2.3Collisions between photons and matter are so rapid that equilibrium is continually re-established despite the steady fall in temperature. At early times the temperature becomes arbitrarily high; we can see why the theory is often called the Hot Big Bang.

Figure 2.6: A collision between an electron and a positron in the LEP collider at CERN leads to a spray of particle-anti-particle pairs created by the energy of collision. (Credit: Opal Collaboration).

At temperature T particles have typical energies k_BT, usually expressed in electron volts: 1 eV = 1.6×10^-19 J is the energy of an electron accelerated through a potential difference of 1 volt. Early enough in the Universe, k_BT is larger than the rest mass energy, m₀c², of any fundamental particle, so collisions resemble those seen in the particle accelerators of high-energy physics (Fig. 2.6). High-energy collisions typically produce a spray of new particles created from the energy of collision, so even if we started with just neutrons and photons, for instance, as Gamow assumed, these would almost instantly be converted into a mixture of every type of particle; to put it another way, we do not have to speculate about the nature of the primordial matter because its composition is determined by the temperature. Most types of particle are paired with an anti-particle, which has equal mass and equal but opposite values of conserved quantities like charge. Both particles and anti-particles can be created in collisions, and when a particle collides with an anti-particle of the same type they annihilate, creating a pair of photons or sometimes another particle-antiparticle pair. In equilibrium, production and destruction rates are equal and each particle type will have a definite thermal distribution of energies, similar but not identical to the black-body spectrum of photons. For each type the total energy density is proportional to aT⁴ times a numerical factor of order unity.

From the information in the previous paragraph, show that all types of particles must be present in roughly equal numbers.

Answer

The energy density is equal to the number of particles per unit volume (n), multiplied by the average energy of each particle. Since all particle types have roughly the same energy density, around u = aT⁴, and roughly the same energy, around E = k_BT, their number density n = u / E must also be roughly the same.

Now recall that for the Friedman equation, `radiation' includes any particles with energies much higher than their rest mass, and in the thermal bath of the early universe this is true for all particle types (and their anti-particles). The total radiation density is

u_r = $${g(T) \over 2}$$aT⁴

where g(T) is the effective number of different types of particles present at temperature T. (Photons count as two types as they can have two polarizations; this gives the conventional u = aT⁴ for photons alone). According to the standard model of particle physics, the maximum value of g(T) is about 106, but this is a lower limit because it only includes known particles. At any rate, this shows that at early times photons themselves contribute only a small part of the radiation density.

2.3.2 The Big Freeze

The history of the Universe is characterised by frantic activity at the very beginning, with events taking place more and more slowly as time goes on (contrast this to human history, which seems to be exactly the opposite!).

Extrapolating the expansion of the Universe backwards using the Friedman equation we find that at t = 0 the temperature and density become literally infinite. Perhaps t = 0 marks the beginning of time; more likely, the Friedman equation, and GR itself, break down at some enormous temperature; it is most honest to admit that our theories cannot cope with the earliest phases of the Big Bang. Moreover, in Section 2.5.3 we will see that there is some evidence that in this shadowy period there was an episode called inflation which would have blotted out any hint of earlier times. We will therefore start our story some time after inflation finished, but still just a tiny fraction of a second after t = 0.

As the universe expands and the temperature falls, there comes a time for each type of particle when its rest mass energy cannot be supplied by typical collisions (which release E $\sim$ k_BT), and so production of that particle type ceases. Normally the particle will then rapidly vanishes from the cosmic mix, because whenever particle and anti-particle collide they annihilate each other. This will change the value of g(T). Now we have a situation when particle number per co-moving volume is not preserved: while g(T) is changing, we no longer have $\rho_{r}^{}$ $\propto$ R^-4, so the expansion of the universe changes gear. The energy carried by the disappeared particles is dumped into those remaining; normally the annihilation is slow enough that this does not actually increase the temperature, but it does reduce the rate of decline. After annihilation is complete, expansion returns to the normal rule, R $\propto$ $\sqrt{t}$, but with a slight offset in the start time caused by the hiccup when g(T) changed. (Since all this happens in the first second, the offset is negligible for practically all purposes).

In this way, each stage of the expansion is characterised by the particle types that were present (Fig 2.7 and Table 2.1). At very early times this is very speculative but as the temperature falls the energies come within the range of experiment and our theory is on firmer ground. At around 10^-12 seconds after the Big Bang we have the full set of known fundamental particles: quarks, which are the components of protons and similar particles, leptons, including electrons and neutrinos, and the particles which carry forces between these, including photons, the carriers of electromagnetism, and gluons, which carry the strong force that binds the quarks. This mix is known as a quark-gluon plasma, as quarks and gluons are the majority particles. By 10^-5 seconds the heavier quarks and leptons have annihilated, leaving the two light quarks (up and down), electrons and their heavier cousins muons, and neutrinos. At this time the temperature becomes low enough for the quarks and gluons to bind together to make protons (two ups and a down quark), neutrons (two downs and an up), pions (a quark-anti-quark pair) and their anti-particles. Quark triplets like protons and neutrons are called baryons. Although these two are the lightest baryons, they are still much heavier than their constituent quarks. In fact their mass energy, m₀c² $\approx$ 1 GeV, is significantly greater than k_BT at the time they form, and so they immediately annihilate. This is the start of the lepton era, when the majority particles are electrons, muons and neutrinos. Our existence shows that baryonic annihilation was not complete, so there must have been a very small excess of quarks over anti-quarks, which observations put at about 1 in 10⁹. The origin of this excess is called baryogenesis, and it remains one of the great unsolved problems in cosmology. In a sense, every baryon in our body is a tiny droplet of the quark-gluon plasma, left over from just 10^-5 seconds after the Big Bang.

Figure 2.7: Schematic diagram of the eras of the Big Bang. The boundaries are over-simplified! Click on image to get a larger-scale version. (Credit: CERN)

Another process now came into play. The reduction in density as the Universe expands reduces the number of `collisions' between particles. Of course particles are not hard spheres; by collision we mean a close-range interaction between two particles, which is mediated by one of the fundamental forces of nature; the known ones are electromagnetism, the strong nuclear force, and the weak nuclear force. The range at which the interaction becomes `close' is smallest for the weak force and largest for electromagnetism. Each type of particle feels one or more of these forces: baryons feel all three, electrons only the electromagnetic and weak, and neutrinos only the weak force. For neutrinos, about a tenth of a second after the Big Bang the chance of another collision falls to less than once in the age of the universe. This point is called freeze out. Freeze out can happen to any particle but it affects neutrinos first (of the ones we know) because the very short range of the weak force means that these interactions are the first to become unlikely. After neutrinos freeze out, they are no longer in thermal contact with the other types of particles. At first this has no effect because, as we have seen, the temperature declines because of the direct effect of the redshift in exactly the same way as for a radiation-dominated universe in thermal equilibrium. Much later it allows the neutrinos to survive long after k_BT falls below their rest mass, because there are no collisions to annihilate them. A similar process is assumed to have happened to the unknown particles which make up the cold dark matter, except that the CDM particles must have mostly annihilated before they froze out, as they are much less numerous than neutrinos.

If the dark matter was dominated by neutrinos, so that $\Omega_{\nu}^{}$ $\approx$ 1 shortly after matter-radiation equality, show that neutrinos would have been just becoming non-relativistic at the time of matter-radiation equality. Because of this property neutrinos are known as Hot Dark Matter. By definition CDM particles became non-relativistic long before matter-radiation equality. Hence show that CDM particles must be much less numerous than neutrinos.

Answer

We have seen that neutrinos carry about the same energy as the photons as long as they are highly relativistic, i.e. k_BT mc²; while this is true, both neutrino and photon energy density falls proportional to R^-4. On the other hand when k_BT mc², the neutrino energy is dominated by the rest mass, and neutrinos behave as matter, with energy R^-3, i.e. falling less rapidly than for photons. If the dark matter is dominated by neutrinos, they will quickly take over from photons as the main carriers of energy once they begin to behave more like matter than radiation, so the condition k_BT mc² must be just beginning to break down, in other words the neutrinos are just becoming non-relativistic.

At matter-radiation equality we have

number density of photons × energy per photon n_photon × 3k_BT_eq

= number density of WIMPs × energy per WIMP n_WIMP × m₀ c²

To say the WIMPs are cold means m₀c ² k_BT _eq, in which case we have

n_WIMP/n_photon 1

and so the number density is much less for WIMPs than for photons, which are about as numerous as neutrinos.

Table 2.1: Key events and periods in the early history of the Universe

Era	time	T (K)	kBT	Comment
Inflation	??	??	??	Inflation, if it happened, wipes the slate clean so that no traces of the earlier universe remain. Any processes which have an effect on our universe must happen after inflation ends.
???	< 10-12 s	> 1016	> 1 TeV	Two processes which must have occurred in the very early universe (but after inflation) are baryogenesis and the decoupling of cold dark matter particles.
Quark-Gluon	10-12 s	1016	1 TeV	Highest energy measured in the lab, and so the earliest time at which our extrapolations are reliable.
	10-5 s	2×1012	200 MeV	Quark confinement: formation of baryons and pions, immediately followed by annihilation of nearly all baryons.
Lepton				Electrons, muons, neutrinos & pions dominate.
	10-4 s	1012	100 MeV	Annihilation of muons and pions.
	0.1 s	3×1010	3 MeV	Neutrino freeze-out
	0.1 s	3×1010	3 MeV	Weak force reactions start to convert neutrons to protons.
	1 s	1010	1 MeV	Electron-positron annihilation.
Photon				Photons and neutrinos dominate, but photons still strongly interact with the baryons and electrons, forming a photon-baryon fluid.
	1 s	1010	1 MeV	Weak force freezes out, stopping conversion of neutrons to protons.
	100 s	109	0.1 MeV	Free neutrons begin to decay to protons.
	500 s	8×108	70 keV	Nucleosynthesis: remaining neutrons combine with protons to make atomic nuclei, mostly Helium-4.
	5 days	2×107	2 keV	Thermal decoupling: electron-proton collisions no longer energetic enough to make new photons; the observed photons of the CMB were created at this time.
	40 yrs	4×105	40 eV	Electron-photon collisions become too weak to significantly change the energy of the photon, only the direction. The spectrum of the CMB is unchanged (except for redshift) from this time.
	60,000 yr	8000	0.7 eV	matter-radiation equality: the radiation density falls to the point that it is equal to the rest mass energy density of the (mostly dark) matter.
Matter
	250,000 yr	4000	0.35 eV	Recombination: electrons combine with protons and alpha-particles to make Hydrogen and Helium atoms.
	400,000 yr	3000	0.26 eV	Last scattering: so few free electrons are left that photons can travel unhindered. Observed CMB photons have travelled in a straight line to us since this time.

About a second after the Big Bang, k_BT falls to 0.5 MeV, the rest mass of electrons and their anti-particles, positrons, and these too annihilate, again leaving a small residue equal in number to the protons. This is the beginning of the photon era as photons and the decoupled neutrinos now carry nearly all the energy. The energy released by electron-positron annihilation is delivered almost exclusively to the photons, and from this point on the photons have a temperature 1.40 times greater than the neutrinos.

The effective number of types is (21/4) for neutrinos and, as stated earlier, 2 for photons. Calculate the relative energies carried by photons and neutrinos after electron-positron annihilation.

Answer

The formula for energy density is u = gaT⁴/2, so

u_photon/u = (g_photon/g)×(T_photon/T)⁴ = ×1.40⁴ = 8×3.84/21 = 1.463.

Alternatively, neutrinos carry 68% of the energy of photons (= 1/1.463).

From this point on we don't believe that any extra energy has been added to the photons, so the redshift for any later stage can be calculated from the temperature: (1 + z) = (T/T_CMB).

2.3.3 Nucleosynthesis

Around 4 minutes after the Big Bang the temperature is low enough for neutrons and protons combine to form atomic nuclei, as originally predicted by Gamow. Nearly all the neutrons end up as helium-4 nuclei (⁴He, also known as $\alpha$ particles), consisting of two neutrons and two protons (2n + 2p). The left-over protons can now be thought of as hydrogen nuclei.

The relative abundance of hydrogen and helium is a key prediction of the Big Bang. At the time protons and neutrons first formed, there were equal numbers of each, so we might expect 100% helium. But several processes tend to convert free neutrons to protons (with an electron as by-product to conserve charge). If these had run too far, we would have 100% hydrogen. These processes stop once the neutron is locked up in a nucleus, so there is a race between neutron conversion and nucleosynthesis. The final answer depends slightly on the number of baryons per photons, usually denoted $\eta$ (eta), but for any reasonable baryon density in the universe today, between one in ten and one in six of the remaining baryons should be a neutron, so helium will make up between 20 and 33% by mass of the baryonic matter. Observations show that the primordial helium abundance is 24±1 %.

2.3.3.1 Baryometers

From the observed helium fraction we can work back to find the baryon-to-photon ratio, $\eta$. Observations of the CMB tell us precisely the current number density of photons, so this should tell us the current baryon density: n_baryon = $\eta$n_photon, and $\rho_{\rm baryon}^{}$ = m_pn_baryon. To convert this into a value for $\Omega_{b}^{}$, we need a value for the Hubble constant, and as mentioned in Section 1.3.3 the convention is to use the fudge factor h = H₀/(100kms^-1Mpc^-1), so the actual density $\rho$ can be converted to a value for $\Omega$h² = $\rho$/($\rho_{c}^{}$/h²).

The baryon density estimated from helium is not very accurate, because the helium abundance doesn't change by much for large changes in the baryon density (this is why the helium abundance is a good test of the Big Bang model: there is no escape if the answer comes out wrong).

Figure 2.8: Abundances of the light elements predicted by the theory of Big Bang Nucleosynthesis, as a function of $\Omega_{\rm baryon}^{}$h². The vertical coloured bars show the values implied by various observations.

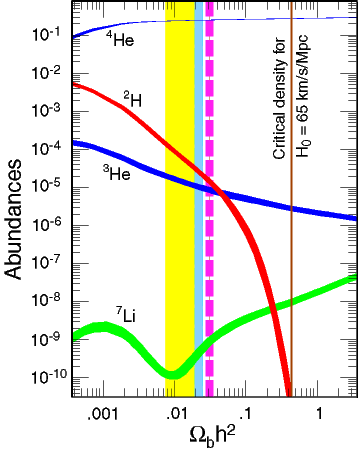Fortunately, not every neutron ends up in ⁴He. Deuterium (n + p) and ³He (n + 2p) are involved in the production of ⁴He and some is left over because nuclear reactions freeze out before conversion to ⁴He is complete. A minute amount of ⁷Li (4n + 3p) is produced in reactions between ⁴He nuclei which freeze out almost before they get started. As with helium, the precise abundances are controlled only by the baryon-to-photon ratio (see Fig. 2.8), but for these nuclei the dependence is much stronger, so that accurate measurements of the primordial abundances should give accurate values of the baryon density. The trick is to find truly primordial abundances. Deuterium is a delicate nucleus and easily destroyed, so over the history of the universe its abundance should steadily decrease. ⁷Li is also easily destroyed, but also created when cosmic rays smash into heavier atoms in interstellar space or on the surfaces of stars. And helium (both isotopes) is both created and destroyed in stars. A great deal of work has gone into searching for places where the abundances of these elements are close to primordial values: ⁷Li and ³He on the surfaces of the oldest stars in our Galaxy, ⁴He in gaseous nebulae of nearby galaxies which seem to show minimal processing by stars. Deuterium is probably the favourite as any detection provides at least a lower limit to the primordial value. Recently, absorption lines of deuterium have been detected at high redshift (z > 2) in the light of distant quasars. These lines are believed to be due to gas discs of newly-formed galaxies intervening between us and the quasar.

A few years ago it was often stated that the various measurements of the abundance of helium, deuterium and lithium were in good agreement, giving a baryon-to-photon ratio of $\eta$ $\approx$ 3×10^-10. Unfortunately, as more data has been gathered and error bars are reduced, the agreement has evaporated, although all techniques give values in the range 2.8 to 6.9×10^-10. The rough agreement strongly suggests the theory is on the right track (otherwise these values could differ by orders of magnitude). It is very likely that there are still systematic errors in at least some of the measurements.

These values correspond to 0.01 < $\Omega_{b}^{}$h² < 0.025.

2.3.4 The origin of the Cosmic Microwave Background

After electron-positron annihilation, photons and neutrinos dominate the energy density of the universe. From their point of view, nucleosynthesis has no discernable effect, as baryons at this time are only a tiny trace constituent of the cosmic plasma. Neutrinos, in fact, are unaffected by anything except gravity. Neutrinos with mass will by now have settled into the gravity wells of clusters and groups of galaxies, but if any neutrino type is genuinely massless it will still be travelling at the speed of light, and if we could build a telescope to detect it, we would see the Universe exactly as it was 0.1 seconds after the Big Bang, at the time of neutrino decoupling. Photons also are unaffected by each other, but they do interact with charged particles such as electrons and atomic nuclei, and this gives the ordinary matter in the universe an unexpected importance. In the photon era, photons can travel only a tiny distance before colliding with an electron^2.4and electrons and nuclei are also constantly colliding. This ties photons, electrons and nuclei into a photon-baryon fluid; one consequence is that the matter particles are kept at the temperature of the photons throughout the expansion, even though, left to themselves, their temperature would drop faster because matter and photons have different equations of state. We will later be interested in the sound speed in this fluid. For a conventional fluid the sound speed c_s $\approx$ $\sqrt{P/\rho}$. In our case, the pressure P = $\rho$c²/3 (c.f. Section 1.3.2), giving

c_s = $${1 \over \sqrt{3}}$$c

which happens to be the exact result for a relativistic fluid, i.e. one where most of the particles have v $\approx$ c.

At first, electron-proton collisions frequently emit photons, and photons are absorbed in the inverse to this process, so an individual photon has a very short life. But after about five days, the frequency of electron- proton collisions becomes negligible; from this time on, photons are neither emitted nor destroyed, and therefore the photons we see in the CMB today were created about that time (if this seems dramatic, remember that the hydrogen nuclei in your body were created 10^-5 seconds after the Big Bang!). We call this the time of thermal decoupling.

Because photons outnumber protons by more than 10⁹:1, collisions between photons and electrons are still very frequent. When a noticeable amount of energy is transferred, we describe the collision process as Compton scattering. If there was a significant difference in temperature between electrons and photons, heat would flow from the hotter to the cooler as you would expect. When the electrons are cold, the photons lose a fraction of order h$$\nu$$/m_ec² of their energy in each collision, where m_e is the electron rest mass. When the electrons are hot, each collision increases or decreases the photon's energy by a fraction of order v/c; on average there is a net gain^2.5 of order (v/c)².

In thermal equilibrium these two factors must be equal and opposite as there is no heat flow between things at the same temperature. You can easily see that this works to order of magnitude:

$${1\over 2}$$m_ev² $$\approx$$ k_BT $$\approx$$ h$$\nu$$ $$\Rightarrow$$ $${v \over c}$$ $$\approx$$ $$\sqrt{2 k_B T \over m_e c^2}$$ $$\approx$$ $$\sqrt{2 h\nu \over m_e c^2}$$

At thermal decoupling, k_BT/m_ec² is around 0.004, giving v/c $\sim$ 0.1. After many collisions where the energy changes by 10% a photon will have a very different energy from its initial value: in general, energy makes a random walk around the typical value of k_BT. If all this takes place in thermal equilibrium, the net effect on the overall spectrum is zero because each photon boosted is matched by another which loses energy. In Section 2.4.2 we look at what might happen if equilibrium breaks down.

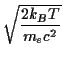
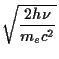
As the universe cools and the typical speed of the electrons drops, energy changes become smaller and smaller, and after about 40 years the stage is reached where all subsequent collisions will have only a minor effect on the energy of each photon; we now have Thomson scattering in which the photon energy is conserved. From this time on the spectrum of the CMB cannot be modified by interaction with matter, and so the observed spectrum should be exactly as it was then, apart from the overall redshift.

Almost nothing further happens until, after about 60,000 years, the density of radiation falls to equality with the rest-mass density of the matter, principally the cold dark matter (CDM) that until this point has had no rôle in our story. This is the start of the matter era. Now we are out of the radiation era we need some observational input to make detailed calculations; for instance, to get the time of matter-radiation equality, we need the present-day matter density, $\propto$ $\Omega_{m}^{}$h². I have assumed $\Omega_{m}^{}$ $\approx$ 0.3, h $\approx$ 0.65, which gives T_eq = 8300 K. After this time, the expansion law tends to the matter-dominated case a $\propto$ t^2/3; but the transition is very smooth. Note that although CDM now dominates the total density, photons continue to dominate the density in the photon-baryon fluid, as only 10-20% of the matter is baryonic. As a result, the sound speed remains close to the relativistic limit c/$\sqrt{3}$.

The end of the `early universe' period comes when the temperature falls to the point that electrons prefer to bind to nuclei to form atoms, rather than floating freely in an ionized gas. Because of its analogies with the astrophysics of nebulae, this is known as the time of recombination although of course the electrons had never combined before! Roughly half the electrons have combined when the temperature reaches 3500 K, but the real end comes a little later, when the universe is about 400,000 years old. At this point so few electrons remain that the photons finally can travel unhindered: the probability distribution for the last scattering of a photon is a normal distribution centered on 2880 K, with standard deviation of 7.5% (this temperature is quite precisely known and is independent of the uncertain matter and baryon densities, unlike the ages I have quoted). That is, the CMB photons we see have travelled in a straight line from this surface, or more correctly thin shell, of last scattering. This is, in effect, the visible surface of the Big Bang. Of course it is a surface in time, not space: we see it as a shell surrounding us because we can only see along our light-cone so the time of last scattering appears at a particular distance from us.

Calculate the redshift of the surface of last scattering given the quoted temperature.

Answer

Given the present CMB temperature of about 3 K, and the fact that temperature falls with redshift as (1 + z)^-1, the redshift of the last scattering surface must be 1 + z 2880/3 1000, i.e. z 1000. The precise present temperature is 2.725 K, giving z = 1056.

The co-moving distance to the surface of last scattering is essentially the same as to the particle horizon (c.f. Section 1.3.4); the 400,000 year interval between the Big Bang and last scattering is only $\sim$ 3×10^-5 of the age of the Universe. Essentially all the volume of the observable Universe is between us and last scattering, and so is observable in practice as well as in principle.