In a cavity (e.g. an oven) with opaque walls all at the same temperature, emission and absorption of photons will eventually come into balance. Then it turns out that in any small region we will find statistically equal numbers of photons travelling in any direction, with the number at each frequency depending only on the temperature. In other words, the temperature fixes
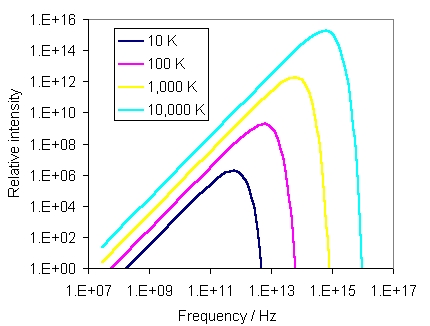 |
Although photons with all frequencies are present in the Planck spectrum,
most have energies h![]() close to 3kBT (in general,
the energy per particle in anything at temperature T is roughly kBT).
close to 3kBT (in general,
the energy per particle in anything at temperature T is roughly kBT).
If you are not in a constant-temperature oven, how much you shine
(your intensity or surface brightness)
depends on three things: your temperature,
how easy it is for photons to go through your surface rather than
bounce off (your albedo), and your transparency.
We quantify transparency
by optical depth, ![]() : defined so that e-
: defined so that e- ![]() is
the probability that a photon will pass right through you rather than be
absorbed. We have already met this
concept in the rather different context of gravitational lensing.
Objects with
is
the probability that a photon will pass right through you rather than be
absorbed. We have already met this
concept in the rather different context of gravitational lensing.
Objects with
![]()
![]() 1 are said to be optically thick.
1 are said to be optically thick.
Let's put a partially transparent slab in our oven and look through it
at the oven walls.
A fraction
(1 - e- ![]() ) of the radiation entering from behind is
absorbed; but in thermal equilibrium the net radiation must be unchanged,
so the slab must emit with a brightness
) of the radiation entering from behind is
absorbed; but in thermal equilibrium the net radiation must be unchanged,
so the slab must emit with a brightness
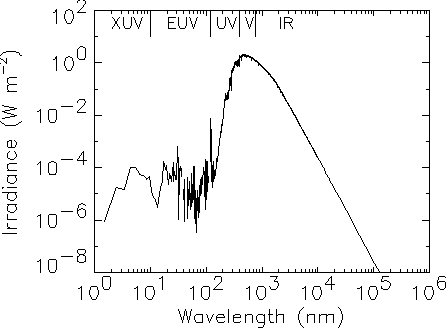
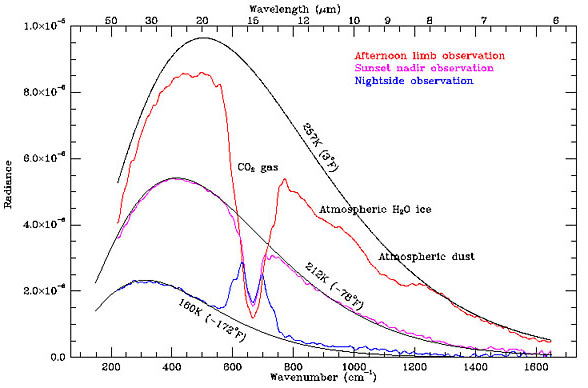
A few astronomical objects have spectra which are very roughly given by black bodies, such as stars and planets (Fig. 2.2). But the spectra are more complicated than ideal black bodies for many reasons. For instance, the Sun contains many layers with different temperatures, which are more or less transparent at different frequencies. We see a narrow absorption line when a cool outer layer that is usually transparent becomes partially opaque at a particular frequency, so that the brightness near that frequency drops towards the value for the cool layer instead of the hot surface beneath. Similarly, the corona is a hot layer that is mostly transparent, but shows bright emission lines at particular X-ray frequencies where the optical depth is relatively high.
|
|
 |
As the name suggests, it takes a lot of stuff to generate a high optical depth, especially across a wide range of frequencies rather than in a narrow line. So it is not surprisingly that space is usually very transparent (of course stars and planets fill a negligible volume of space).
2.1.2 Temperature and BrightnessThe formal SI units for surface brightness or intensity I(
B(
Usually there is no connection between TPB and the
physical temperature of the emitting object, since real black bodies are
very hard to find.
In radio astronomy it is more common to use a variant form of brightness temperature which, instead of the Planck law, uses the Rayleigh-Jeans law,
BRJ(
The Rayleigh-Jeans brightness
BRJ(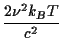
AnswerUse the approximation to simplify the denominator in the formula for the black body curve: exp Hence B(
This is the formula for BRJ.
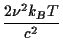 |
This result is not too difficult to derive. As redshifting just stretches the spectrum, the shape will be preserved, but the peak wavelength will be longer by a factor of (1 + z). We saw that in a black body,
Finally, if photons are travelling in equal numbers and with the same distribution of energies in all directions (i.e. the intensity is isotropic), then the energy density in photons is
In 1917 the French astrophysicist Charles Fabry published a quirky paper which nicely illustrated some concepts related to black body radiation. What, asked Fabry, is the temperature of empty space? That is, if an object was placed in space, what temperature would it settle down at? Clearly, it would absorb starlight, and also emit its own thermal radiation. The equilibrium temperature would be the one where the energy gain from absorption was equal to the loss from emission. Fabry's point was that there was no well-defined answer to his question: the equilibrium temperature would depend on the physical properties of the object, much more than on the amount of starlight in space which one might have thought would define some sort of effective temperature.
For instance, if the object was a black body
it would absorb all incident photons and so
the equivalent temperature would be that of a black body cavity containing
the same radiation density as space. For interstellar space in our Galaxy
he calculated this to be 3o absolute, or 3 K in modern notation.
But unlike a black body cavity, the spectrum arriving at the object would
be very different from the one leaving it: starlight is in the visible band
(wavelength
![]()
![]() 500 nm), while the Planck spectrum at 3 K
peaks at
500 nm), while the Planck spectrum at 3 K
peaks at
![]()
![]() 1 mm, on the border
between the radio and the infrared. Roughly speaking, starlight has the
spectral shape of a black body at around 6000 K, but an intensity 1013
times less, essentially because only about one part in 1013 of the sky
is actually covered by the surfaces of stars
(for a position inside a galaxy; the value is far smaller in intergalactic
space).
1 mm, on the border
between the radio and the infrared. Roughly speaking, starlight has the
spectral shape of a black body at around 6000 K, but an intensity 1013
times less, essentially because only about one part in 1013 of the sky
is actually covered by the surfaces of stars
(for a position inside a galaxy; the value is far smaller in intergalactic
space).
Now suppose the object was good at
absorbing visible light but had a high albedo near ![]() 1 mm, so that
it radiated much less than a black body at that wavelength. The incoming
energy would heat it until eventually emission
matched absorption despite the poor radiative efficiency (we now call this
the Greenhouse Effect). If absorption and emission were confined to
only a single wavelength in the visible band, the body would have to shine
in visible light to get rid of its excess heat; the equilibrium temperature
would be the Planck brightness temperature at the wavelength of
absorption, which is around about a thousand degrees in the visible band
in interstellar space. Atoms and simple molecules do absorb at only
a small number of discrete wavelengths, and so they can reach very high
excitation temperatures in interstellar space (which is why they
are often ionised).
By the same token, if the object was a poor absorber of visible light
and a good radio emitter, it could cool to whatever the radio brightness
temperature was; almost negligibly small, as far as Fabry knew.
1 mm, so that
it radiated much less than a black body at that wavelength. The incoming
energy would heat it until eventually emission
matched absorption despite the poor radiative efficiency (we now call this
the Greenhouse Effect). If absorption and emission were confined to
only a single wavelength in the visible band, the body would have to shine
in visible light to get rid of its excess heat; the equilibrium temperature
would be the Planck brightness temperature at the wavelength of
absorption, which is around about a thousand degrees in the visible band
in interstellar space. Atoms and simple molecules do absorb at only
a small number of discrete wavelengths, and so they can reach very high
excitation temperatures in interstellar space (which is why they
are often ionised).
By the same token, if the object was a poor absorber of visible light
and a good radio emitter, it could cool to whatever the radio brightness
temperature was; almost negligibly small, as far as Fabry knew.
Fabry's argument was included in Arthur Eddington's famous book The Internal Constitution of the Stars, and in this form was transmitted to later generations of astronomers. Eddington made the point in a slightly different way, choosing to define the temperature of space as the equivalent black-body temperature, 3 K, and only later showing by example that this was a fairly meaningless number. This re-arrangement had a disastrous effect, as we will see, because casual readers tended to pick up only the first part of the argument.