1.4 Observational cosmology
The fate of the Universe is controlled by
the parameters ![]() ,
, ![]() , and
, and ![]() which, according to current theories, define the composition
of the "stuff" that makes up our Universe. The quest for these three
numbers takes up a large fraction of observational cosmology. In this search, a
wide range of techniques from physics and astronomy have been brought to bear;
we have already seen how gravitational lensing has been used to search for
MACHOs and to measure the dark matter in clusters of galaxies. Later in this
segment we will examine in detail methods using the Cosmic Microwave
Background. Here we quickly review the other important methods.
which, according to current theories, define the composition
of the "stuff" that makes up our Universe. The quest for these three
numbers takes up a large fraction of observational cosmology. In this search, a
wide range of techniques from physics and astronomy have been brought to bear;
we have already seen how gravitational lensing has been used to search for
MACHOs and to measure the dark matter in clusters of galaxies. Later in this
segment we will examine in detail methods using the Cosmic Microwave
Background. Here we quickly review the other important methods.
1.4.1 The particle zoo
To start with, what can physics tell us about the contents of the Universe? There are hundreds of different types of subatomic particles known, but most of them disintegrate in a fraction of a microsecond. In cosmology we are only interested in stable particles, and this gets us down to the following:
- electrons
- protons
(which are, of course, the nuclei of hydrogen atoms)
- neutrons;
on their own, neutrons disintegrate in about 11 minutes, but they can be
stable if bound together with protons in the nucleus of an atom.
- three
different flavours of neutrino (each with its anti-neutrino).
- photons.
In addition to particles, gravitational waves may contribute a significant energy density to the Universe, especially at early times.
Protons and electrons are equally numerous: there is no net electric charge in the Universe; otherwise, electric repulsion would overwhelm gravity, and planets, stars and galaxies would disintegrate (or rather, could never form). Cosmologists refer to ordinary matter made of electrons and atomic nuclei as baryonic matter (a misuse of a term from particle physics). In principle anti-matter, made of anti-protons, etc., is also stable, but if there was any significant amount of it in our Universe we would see a lot more gamma-rays from matter-anti-matter annihilation.
Neutrinos are the lightest known stable particles, apart from photons. They have no electric charge and only interact with each other and other types of matter via gravity and the weak nuclear force, which makes them very hard to detect. For a long time it was thought that they had zero rest mass, and therefore, like photons, moved at the speed of light. Within the last year it has been confirmed that neutrinos do have a finite mass, which means that as they lose energy in the expansion of the Universe they should eventually become non-relativistic and count as matter.
In other words, according to known physics, the
stuff in the Universe consists of baryonic matter (which contributes to ![]() ), photons and gravitational waves (which contribute to
), photons and gravitational waves (which contribute to ![]() ), and neutrinos and anti-neutrinos (which contribute to
), and neutrinos and anti-neutrinos (which contribute to ![]() at early times and later to
at early times and later to ![]() ).
).
1.4.2 Photons (and neutrinos)
We
can directly observe the photon content of the Universe. Ninety percent of the
photon energy is in the Cosmic Microwave Background, which has an energy
density of 4.20×10-14 Jm-3, corresponding to ![]() = 1.22×10-5. This is
negligible today but these photons have been conserved since the Big Bang, and
extrapolating back in time they become very important at z > 104. The other 10% of the photon
energy density has been generated by stars and quasars over the history of the
Universe. These photons tell us everything we can know about the early history
of the galaxies, but their energy density has always been negligible, because
the earliest of these photons were generated after z
= 1.22×10-5. This is
negligible today but these photons have been conserved since the Big Bang, and
extrapolating back in time they become very important at z > 104. The other 10% of the photon
energy density has been generated by stars and quasars over the history of the
Universe. These photons tell us everything we can know about the early history
of the galaxies, but their energy density has always been negligible, because
the earliest of these photons were generated after z ![]() 10.
10.
According to big bang theory, neutrinos and
antineutrinos should have nearly matched photons for energy density in the
early Universe: ![]() = 0.681
= 0.681![]() . Using the lower limit for the neutrino mass from recent
experiments, the present
. Using the lower limit for the neutrino mass from recent
experiments, the present ![]() > 10-3; on the other hand, almost certainly
> 10-3; on the other hand, almost certainly ![]() < 0.1, or neutrinos would have had a visible effect on the
large-scale structure.
< 0.1, or neutrinos would have had a visible effect on the
large-scale structure.
1.4.3 Matter
1.4.3.1 Observing Baryons
Stars
are the most obvious form of baryonic matter in the Universe. In the Solar
System, the Sun contains 99.87% of all the baryons, so it was once hoped that a
plausible way of measuring the baryonic density would be to measure the total
amount of starlight and hence work out the typical density in stars. Both the measurement
and the calculation are very tricky, and so it was something of a relief when
it became apparent at the end of the 20th century that in fact the majority of
visible baryons are not in stars but in clouds of intergalactic gas.
For instance, in clusters of galaxies the gas has
a temperature of 107 to 108 K, and emits X-rays
which allow us to measure it quite accurately (Fig. 1.13) The total mass in gas is typically around
ten times the mass in the stars of the galaxies within the cluster. Outside
clusters, the gas is much cooler (≤105 K) and so radiates
much less, but it produces absorption lines in the spectra of distant quasars,
which allows us to estimate the total mass.
|
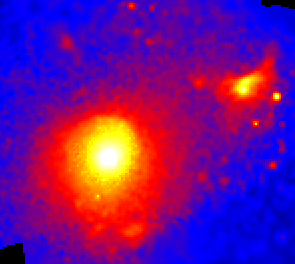
Figure 1.13: A cluster of galaxies as seen through an optical
telescope (left, from the Digital Sky Survey),
which detects starlight from the individual galaxies, and through the ROSAT
X-ray telescope (right) which detects emission from the hot gas between the
galaxies. Most of the baryonic mass in the cluster is in the gas, not the
stars. |
A recent assessment of data on the
"visible" baryonic matter including both stars and gas gave ![]()
![]() 0.02 (Fukugita et al. 1998).
This is dominated by a rather uncertain estimate of intergalactic gas in
typical groups of galaxies like our own.
0.02 (Fukugita et al. 1998).
This is dominated by a rather uncertain estimate of intergalactic gas in
typical groups of galaxies like our own.
1.4.3.2 Weighing the Universe
As well as directly observing radiation from matter, we can track its presence by looking at its gravitational effects. The attempt to do so in other galaxies is described by Strobel, and leads to the conclusion that the large majority of the mass of galaxies is dark matter.
We can apply the same equations on a larger scale, looking at the random motion of galaxies in clusters of galaxies. We can also use atoms in the hot gas in clusters (where we get the speed from the gas temperature, revealed by its X-ray spectrum). In the previous part of this course, we saw that the masses of galaxies and clusters can also be measured via gravitational lensing.
On the largest scales, gravity is not strong enough to overcome the Hubble flow, but can affect it. Galaxies are not scattered at random through the Universe, but form a pattern called the cosmic web which consists of great filaments and sheets of galaxies, separated by voids which seem to contain very little matter (Fig 1.14). Clusters of galaxies form at the joins between filaments. The largest voids are up to 100 Mpc across; only when averaged on scales larger than this is the Universe close to homogeneous. On smaller scales the gravitational force from the dense regions of the cosmic web decelerates the Hubble flow around them, and by the same token increases the flow out of the voids, so there is a net flow of matter from voids to sheets, sheets to filaments, and filaments to the clusters. These flows add "peculiar redshifts" to the cosmological redshift, which can be estimated in two ways. The simple one is to subtract H0r/c from the observed redshift (Fig. 1.15); uncertainties in the distance r make the resulting values rather inaccurate. More subtly, we can analyse the map of galaxies in "redshift space" (Fig. 1.14): peculiar redshifts distort the map in the radial direction only, and we can estimate their amplitude by assuming that in reality the pattern is statistically isotropic. Either way, the amplitude of peculiar redshifts allows us to estimate the density of matter in the cosmic web.
All these techniques agree with each other in
showing that galaxies are embedded in dark haloes which contain hundreds
of times more mass that their visible stars, and so substantially more mass
than the visible baryons, even including the intergalactic gas. By the same
token this matter outweighs the expected neutrino density. Applied to the
largest scales, the estimate is ![]()
![]() 0.35±0.1. What is needed is a form of matter
which can be gravitationally bound to galaxies, and is also undetectable by its
emission or absorption. To bind to galaxies, random speeds of particles must be
less than the escape velocity (typically a few hundred kilometres per second),
so the matter is cold (v « c). We call it cold dark matter,
or CDM.
0.35±0.1. What is needed is a form of matter
which can be gravitationally bound to galaxies, and is also undetectable by its
emission or absorption. To bind to galaxies, random speeds of particles must be
less than the escape velocity (typically a few hundred kilometres per second),
so the matter is cold (v « c). We call it cold dark matter,
or CDM.
This all assumes that Newtonian theory (or GR, which in this context gives the same answers) works on sizes comparable to galaxies and larger. An alternative viewpoint is that the standard theory is an approximation valid on only small scales, and the dark matter is a figment caused by using an incorrect formula. The most developed version of this approach is a theory called MOND, for MOdified Newtonian Dynamics, according to which Newton's 2nd law F = ma breaks down for very small accelerations. Although MOND has been remarkably successful in accounting for the rotation speeds of galaxies, it has not yet proved possible to combine it with other known laws of physics, in particular relativity theory, to make a coherent whole. Most cosmologists find it easier to accept so-far undetected forms of matter than radical revisions to the laws of dynamics. After all, it is not that easy to detect something at a range of thousands of light years.
|
Figure 1.14: A slice through the cosmic web, from the 2dF Galaxy
Redshift Survey. The 2dF instrument on the Anglo-Australian Telescope can
measure 400 redshifts simultaneously. It is being used to observe 250,000
galaxies along two narrow strips on opposite sides of the sky. The plot shows
the positions of the galaxies, placing each at its "redshift
distance" d = cz/H0. The density of galaxies declines at large
distances because only the most luminous galaxies there are bright enough for
their redshift to be measured. Credit: John Peacock and the 2dFGRS team. Click here for a larger-scale
version. |
|
|
|
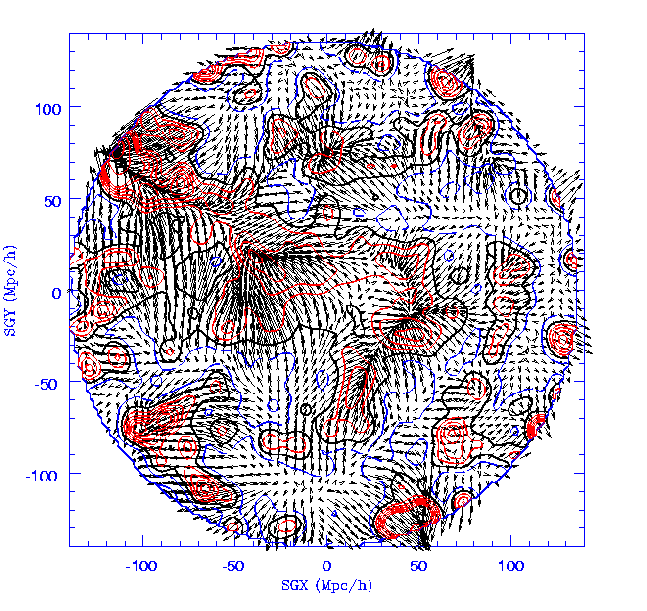
Figure 1.15: The local cosmic flow. This plot represents a slice
through space with our Galaxy at the centre. The vectors show the predicted
peculiar velocities assuming that the local density of matter is proportional
to the density of galaxies. . Click
here for a larger-scale version. |
|
1. To escape the conclusion that there is a lot of dark
matter, would you have to have acceleration greater or less than F/m? Answers to question at end of this document. |
1.4.3.3 Dark Stars?
Could
the CDM be made of baryonic matter? This is very unlikely if the matter is a
thin gas filling a large fraction of space, as gas will almost always be
visible via either absorption or emission. On the other hand, a large number of
dense compact objects such as planets, very low mass stars, burnt-out stars
(i.e. white dwarfs) or black holes, could lock up vast quantities of mass
between them, and yet still be so sparse in space that they never reveal
themselves by blocking out a background star. All of these produce very little
emission for their mass, and would have been missed by the searches for visible
matter mentioned above. They are generically known as MACHOs, for Massive Compact Halo Objects. As we
saw in the course segment on Gravitational Lenses, MACHOs in our Galaxy can be
detected by gravitational microlensing. As mentioned there, the micro-lenses
being detected seem to consist of ordinary low-mass stars or possibly white
dwarfs. This work shows that MACHOs can make up at most about 20% of the dark
halo of our Galaxy.
There are two other lines of evidence which
suggests that MACHOs can account for only a small part of the dark matter.
These are techniques which measure the baryon density in the early Universe,
generically known as baryometers. The first is the theory of Big Bang
nucleosynthesis, (Section 2.3.3)
which predicts that the abundance of helium and other elements formed in the
big bang can be related to the present-day baryon density. This approach yields
![]() h2 = 0.02±0.01. The second baryometer is
based on the pattern of fluctuations in the CMB (Section2.6.2). It gives results in close
agreement with those from big bang nucleosynthesis.
h2 = 0.02±0.01. The second baryometer is
based on the pattern of fluctuations in the CMB (Section2.6.2). It gives results in close
agreement with those from big bang nucleosynthesis.
The baryometer results clearly show that ![]() «
«![]() . They do allow a MACHO density as high as that of visible
baryons, but uncertainties are so large that it is also possible that MACHOs
are negligible compared to the intergalactic gas.
. They do allow a MACHO density as high as that of visible
baryons, but uncertainties are so large that it is also possible that MACHOs
are negligible compared to the intergalactic gas.
1.4.4 The particle bestiary
We are faced with a dilemma: dynamical measures of
mass say that the density parameter is ![]()
![]() 0.35, while combining baryometers with our best
understanding of the (so far undetected) cosmic neutrino background and stretching
the uncertainties to the limit, known particles could contribute only
0.35, while combining baryometers with our best
understanding of the (so far undetected) cosmic neutrino background and stretching
the uncertainties to the limit, known particles could contribute only ![]() +
+ ![]() < 0.15. Almost certainly, any stable particle that was
electrically charged or subject to the strong nuclear force would have been discovered
in the laboratory by now, since they would interact strongly with known
particles. We are therefore looking for a type of particle which interacts with
known matter only via gravity, perhaps the weak nuclear force, and perhaps via
other weak interactions so far undiscovered. The generic name is WIMP,
for Weakly Interacting Massive Particle. WIMPs
would be "dark" by definition, of course.
< 0.15. Almost certainly, any stable particle that was
electrically charged or subject to the strong nuclear force would have been discovered
in the laboratory by now, since they would interact strongly with known
particles. We are therefore looking for a type of particle which interacts with
known matter only via gravity, perhaps the weak nuclear force, and perhaps via
other weak interactions so far undiscovered. The generic name is WIMP,
for Weakly Interacting Massive Particle. WIMPs
would be "dark" by definition, of course.
Particle theorists have invented a large number of particles which fit the bill, such as the axion, axino, gravitino, mirror particle, neutralino, photino, Q-ball, sterile neutrino, sneutrino and more. These so-far imaginary particles appear in theories which attempt to go beyond the "standard model" of particle physics. The standard model explains all known particles and their interactions, but at the cost of several dozen parameters (e.g. particle masses) which have unexplained values, even though they show tantalising signs of some hidden regularity. Since the various particles are predicted by competing theories, at most only a few of them can really exist; and of course there may be real WIMPs which have not yet been thought of. Currently, more than 20 experiments are trying to detect WIMPs from our Galactic halo as they pass through the laboratory.1.2 So far, no clear detection has been made, but this is not surprising as the experiments are so far barely sensitive enough to succeed on the most optimistic predictions.
To cosmologists the various types of WIMP are interchangeable; the particle physics just provides an excuse to include enough matter to explain the dynamical measurements.
1.4.5 Dark Energy
In
1997, the astronomical world was stunned by unexpected results from two
projects to find distant
What does
this tell us? The `expected' distances come from working back assuming the current
rate of expansion, and using the redshift to tell us how much the Universe has
expanded between the time the light left the supernovae and now (the furthest
supernovae were at z ![]() 1, so this was a factor of around two). As the
distance is larger than we thought, the light has taken more time than we
thought to get here; in other words, the Universe took more time to expand from
half its current size than you would expect from the current rate of expansion.
This can only mean that the expansion is getting faster with time, as if there
was some anti-gravity force hurling the galaxies apart; as we have seen, we
label the mysterious stuff that has this effect as dark energy. We have already
seen that the number of gravitational lenses at large distances puts strong
constraints on the quantity of dark energy. In Section 2.6.3 we will see how, combined with CMB
data, all these constraints give a consistent picture in which dark energy
makes up around two thirds of the total present-day energy density in the
Universe.
1, so this was a factor of around two). As the
distance is larger than we thought, the light has taken more time than we
thought to get here; in other words, the Universe took more time to expand from
half its current size than you would expect from the current rate of expansion.
This can only mean that the expansion is getting faster with time, as if there
was some anti-gravity force hurling the galaxies apart; as we have seen, we
label the mysterious stuff that has this effect as dark energy. We have already
seen that the number of gravitational lenses at large distances puts strong
constraints on the quantity of dark energy. In Section 2.6.3 we will see how, combined with CMB
data, all these constraints give a consistent picture in which dark energy
makes up around two thirds of the total present-day energy density in the
Universe.
Answers to questions
1.
To escape the conclusion that there is a lot of
dark matter, would you have to have acceleration greater or less than F/m?
Answer to question
The outer regions of spiral galaxies rotate too fast for the rotation to be explained by the visible matter (c.f. Strobel's notes). To maintain circular motion with speed v requires an acceleration towards the centre of v2/r, so MOND requires a larger acceleration than the prediction of Newtonian theory, a = F/m.
|
|
|
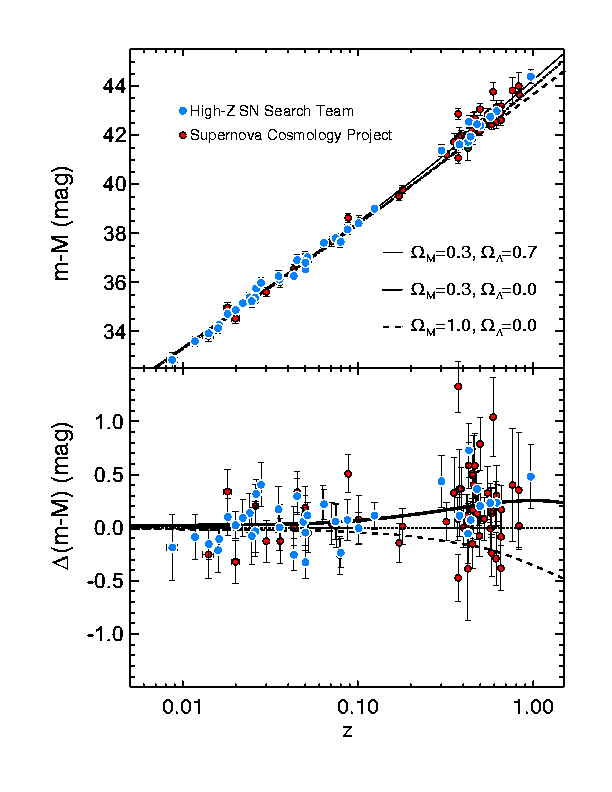
Figure 1.16: The magnitude vs. redshift results for Type Ia
Supernovae. Note that larger magnitude means lower flux density; therefore,
as the supernovae tend to fall above the straight-line extrapolation at high
redshift, they are fainter than predicted. |