This material (and images) is copyrighted!
See my copyright
notice for fair use practices.
The compositions of stars are determined through spectroscopy.
Spectroscopy is the study of something using spectra. Recall from the electromagnetic
radiation chapter that a spectrum is what results when you spread starlight
out into its individual colors. By noting what absorption
lines (or sometimes, emission
lines) are present and their strengths, you can find out a tremendous amount
of information. Stars have absorption lines patterns similar to the Sun. This
means that they are composed mostly of hydrogen and helium with traces of other
elements.
From these absorption lines you learn some important things beside the star's
composition:
- Structure of stars: From the simple fact that you see absorption
lines in most stellar spectra, you know that the stars must have a hot dense
part that produces a continuous spectrum and an outer layer, or atmosphere,
made of cooler, low density gas. The general trend is density and temperature
of stars decreases as the distance from the star's center increases. The hot
dense part is also gaseous because of the extreme temperatures. Stars have no
molten rock in them like the interiors of some of the planets.
- Universality of physical laws: The same pattern of hydrogen lines
are seen in the in spectra of the Sun, stars, distant galaxies, and quasars
(active galaxies at very great distances from us). This is a sensitive test of
whether or not the laws of physics used in the structure of atoms works
everywhere in the universe. Because the same patterns are seen in the spectra,
regardless of where the light comes from, the physics used on Earth must work
everywhere else in the universe! All of the absorption lines seen in celestial
objects can be seen in laboratories on Earth. The charge and mass of the
electron and proton are the same everywhere you look. Physical laws are
the same everywhere!
- Permanence of physical laws: Since light has a finite speed and
the distances are vast, the light received from far away sources has been
travelling for billions of years. The light from those remote regions tells us
about the physical laws way back then. The spectra seen can be explained with
the same physical laws in operation here on Earth at the present time.
Physical laws are the same throughout time!
The Velocities of Stars
The velocity of stars are
determined by using the doppler effect (see the doppler
effect section). The motion of a star causes a shift in the wavelengths
received. The star emits the same spectrum it would emit if it
was at rest. The pattern of lines depends on the internal physics of the star
itself. The doppler effect depends on the external property of the star's motion
through space relative to us. The wavelength shift 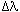 =
= 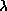 new -
new - 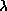 rest, where
rest, where 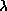 new is the observed
wavelength and
new is the observed
wavelength and 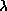 rest is the wavelength you would observe if the star was not
moving relative to us. The amount of the shift depends on the velocity of the
star in this way:
rest is the wavelength you would observe if the star was not
moving relative to us. The amount of the shift depends on the velocity of the
star in this way: 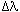 /
/ 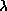 rest = (radial velocity) / c, where c is the
speed of light and the radial velocity is the component of the star's
motion that is along the line of sight. Rearranging the terms you find
the radial velocity = (
rest = (radial velocity) / c, where c is the
speed of light and the radial velocity is the component of the star's
motion that is along the line of sight. Rearranging the terms you find
the radial velocity = (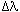 /
/ 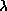 rest) × c.
rest) × c.
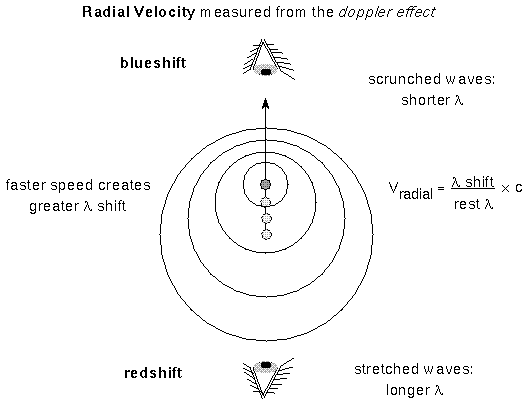
If the star is moving away from you, then you see the wavelengths stretched
out and 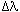 is a positive number. The spectral lines appear shifted to the red end of the
spectrum, so the shift is called a redshift. If the star is moving toward
you, then the wavelengths appear to the compressed and
is a positive number. The spectral lines appear shifted to the red end of the
spectrum, so the shift is called a redshift. If the star is moving toward
you, then the wavelengths appear to the compressed and 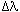 is a negative number. The
spectral lines are shifted to the blue end of the spectrum, so the shift is
called a blueshift. The doppler effect tells you only about the motion
relative to you. If you move toward the star or it moves toward you,
the doppler effect will be the same. The Earth is in motion relative to the star
because it are orbiting the Sun, so you have to take the Earth's orbital motion
into account when figuring the star's velocity from the doppler effect.
is a negative number. The
spectral lines are shifted to the blue end of the spectrum, so the shift is
called a blueshift. The doppler effect tells you only about the motion
relative to you. If you move toward the star or it moves toward you,
the doppler effect will be the same. The Earth is in motion relative to the star
because it are orbiting the Sun, so you have to take the Earth's orbital motion
into account when figuring the star's velocity from the doppler effect.
Also, the doppler effect gives you only the speed along the line of
sight. Most stars move at an angle to our line of sight. The part of a
star's total velocity that is perpendicular to the line of sight is
called the tangential velocity.
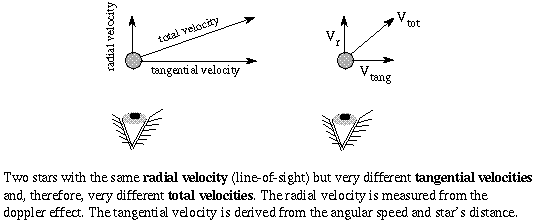
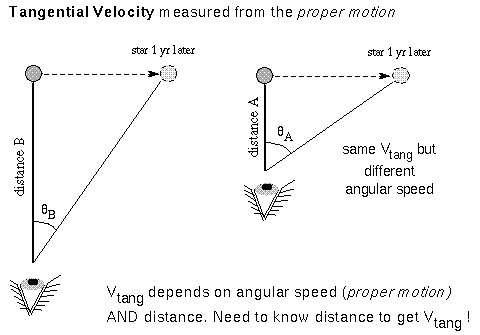
To get the tangential velocity, you need to first measure the angular
velocity of the star across the sky (d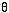 /dt). This is how many degrees on
the sky the star moves in a given amount of time and is called the proper
motion by astronomers. If you determine the star's distance from its
trigonometric parallax or the inverse square law method, you can convert the
angular velocity (proper motion) to tangential velocity in physical units such
as kilometers/second. The tangential velocity = k × the star's distance ×
the proper motion, where k is a conversion factor that will take care of
the conversion from arc seconds and parsecs and years to kilometers/second.
Using the Pythagorean theorem for right triangles, you find that the star's
total velocity = Sqrt[(radial velocity)2 + (tangential
velocity)2].
/dt). This is how many degrees on
the sky the star moves in a given amount of time and is called the proper
motion by astronomers. If you determine the star's distance from its
trigonometric parallax or the inverse square law method, you can convert the
angular velocity (proper motion) to tangential velocity in physical units such
as kilometers/second. The tangential velocity = k × the star's distance ×
the proper motion, where k is a conversion factor that will take care of
the conversion from arc seconds and parsecs and years to kilometers/second.
Using the Pythagorean theorem for right triangles, you find that the star's
total velocity = Sqrt[(radial velocity)2 + (tangential
velocity)2].
Vocabulary
| blueshift |
doppler effect |
proper motion |
| radial velocity |
redshift |
spectroscopy |
| tangential velocity |
Formulae
- redshift:
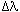 > 0. Object moving away from you.
> 0. Object moving away from you.
- blueshift:
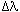 < 0. Object moving toward you.
< 0. Object moving toward you.
- Radial velocity = (
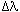 /
/ 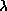 rest) × c, where
rest) × c, where
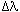 is
the doppler shift,
is
the doppler shift, 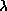 rest is the wavelength you
would see if the star was at rest. The rest wavelength is also the wavelength
of light emitted by the star. Larger doppler shift means greater
radial velocity.
rest is the wavelength you
would see if the star was at rest. The rest wavelength is also the wavelength
of light emitted by the star. Larger doppler shift means greater
radial velocity.
- Tangential velocity = k × (the star's distance) ×
(d
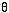 /dt), where k is a conversion factor and (d
/dt), where k is a conversion factor and (d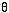 /dt) is the
angular velocity or proper motion of the star.
/dt) is the
angular velocity or proper motion of the star.
- Total velocity = Sqrt[(radial velocity)2 +
(tangential velocity)2]
Review Questions
- How is spectroscopy used to find the composition of stars?
- How do scientists know that the laws of physics are the same everywhere in
the Galaxy and have been the same for billions of years?
- How does the amount of doppler shift in the spectral lines depend on the
relative speed? How does the direction of shift of the spectral lines depend
on the direction of motion?
- Given three stars moving with the same total speed of 40 kilometers/second
but in three different directions: (A) moving away at an angle=45° from our
line of sight, (B) moving directly away from us, (C) moving perpendicular to
our line of sight, put the stars in order of increasing amount of shift you
see in their spectral lines (the smallest shift first).
- The H-alpha spectral line is at 6563Å. Star (A) has that line at 6568Å,
star (B) has that line at 6560Å, star (C) has that line at 6563Å. Which star
is moving the fastest (along the line of sight) and what is the three stars'
directions of motion?
- What must you first know about a star before you can convert its angular
velocity to a tangential velocity in kilometers/second?
- Two stars have proper motions of 0.5 arc seconds/year. Star (A) is
20 parsecs away and star (B) is 30 parsecs away. Which one is moving faster in
space?
- Two stars orbit about a common point in a plane that is oriented parallel
to our line of sight. What will you see happening to the spectral lines of
each star? If there is a change, will both stars' spectra be changing in the
same direction at the same time?
The Masses of Stars
To determine the masses of stars,
Kepler's third law is applied to the motions of binary stars and Kepler's third
law (see the gravity
chapter). Usually the binary stars are spectroscopic binary stars. A
spectroscopic binary system is two stars orbiting a common point at too great a
distance away from us to resolve the two stars individually, but whose binary
nature is indicated in the periodic shift of their spectral lines as they orbit
around each other. Spectroscopic binary stars are used because (a) there are a
lot more far away stars than nearby ones and (b) more importantly, you can
easily measure their speeds from the doppler shifted lines.
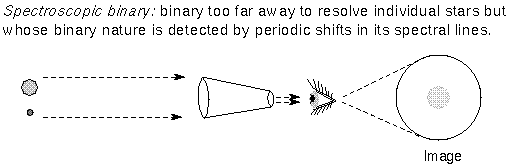
Newton's form of Kepler's third law gives the combined mass of the
two stars: (mass 1 + mass 2) = (separation distance)3/(orbital
period)2 if you use solar mass units, the A.U. for the distance unit
between the stars, and the time unit of years for the orbital period. The total
distance between the two stars is used in Kepler's third law, but their
individual distances from the common point they orbit is used to determine the
stars' individual masses.
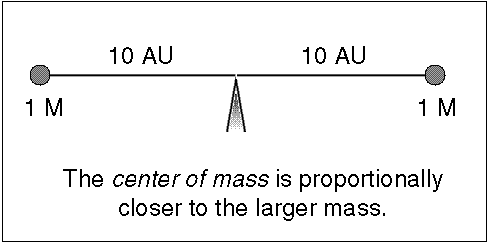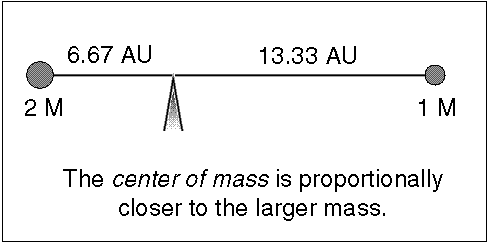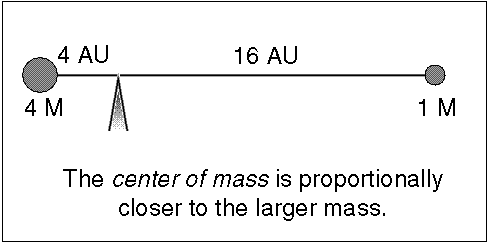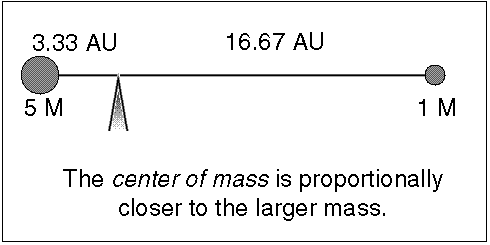
Since stars have about the same mass (within a factor of 20), they both orbit
around a common point, called the center of mass, that is significantly
different from one of the star's center. The center of mass (C.M.) is the
point where (mass star 1) × (C.M. distance 1) = (mass star 2) × (C.M. distance
2), or the point they would be balanced upon if the stars were on a stellar
seesaw (it is the ``x'' in the figure below). The massive star is closer to the
center of mass than the low-mass star and the massive star also moves
proportionally slower than the low-mass star so its spectral lines have a
smaller doppler shift.
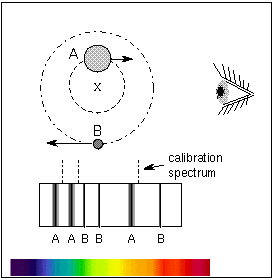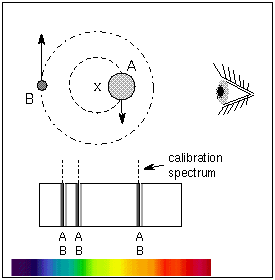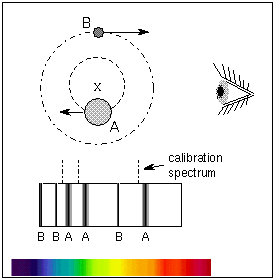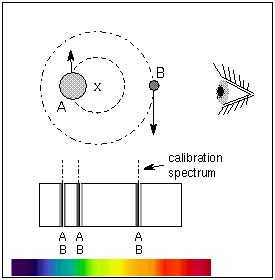
Newton's Law of Gravity explains why this is. The gravitational force exerted
by the massive star causes a large acceleration in the motion of the low-mass
star, so the low-mass star moves faster and has a larger orbit. The weaker
gravity exerted by the low-mass star produces a smaller acceleration on the
massive star, so the massive star's orbital speed is less and its orbit is
smaller. Think about how you could also explain this using Newton's second and
third laws of motion.
The distance travelled by an object = velocity × the
time it takes. The distance travelled by the star is just the
circumference of the orbit = 2p × the radius of a
circular orbit and something similar for an elliptical orbit. Therefore, each
star's C.M.-distance r = the star's velocity × the star's orbital
period / (2p). This allows you to use the easily
measured velocity in Kepler's third law and in the center of mass
relations. The doppler shifts of the spectral lines are used to construct a
radial velocity curve---a plot of the radial velocity (line of sight
velocity) vs. time. The low-mass star will move proportionally faster than the
massive star.
Uncertainty arises, though, if the binary orbital plane is inclined to our
line of sight. In that very common case, the radial velocity = total velocity ×
Sin(inclination angle). The inclination angle i ranges
from i=0° for a face-on orbit (viewing the orbit from directly above the
system) to i=90° for an edge-on orbit (viewing the orbit along its
plane). The inclination angle can be approximately determined from the plot of
radial velocity vs. time. If the binary is an eclipsing binary, then you know
that i=90° because you see them periodically pass in front of each other.
Eclipsing binaries also allow us to accurately determine the diameters of stars
(discussed in the next
section). The radial velocity measurement technique has also been used to
find planets around other stars and to locate black holes from the doppler
shifts they produce in the visible stars they orbit around.
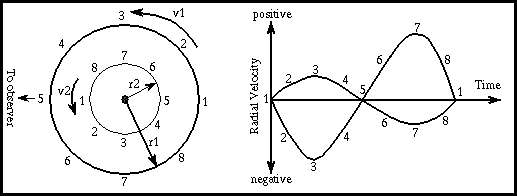
Remember these rules:
- Stars stay on the opposite side of the center of mass from each other.
- The massive star moves slower than the low-mass star.
- The center of mass is also the point where mass1 × velocity1 = mass2 ×
velocity2
Using the distance of the center of mass from each star, you can proportion
out the total mass to each star. Here are the steps to figure out each star's
mass:
- Find the total mass (mass star A + mass star B) from Kepler's 3rd law.
- Find the proportion of each star's mass to the total mass from the center
of mass: (mass star A)/(mass star B) = (C.M. distance B)/(C.M. distance A) or
(mass star A)/(mass star B) = (velocity star B)/(velocity star A). Note which
star's values are on top of the fraction and which are on the bottom! Simplify
the fraction down as far as possible.
- Set the mass of star A = (mass of star B)×(the fraction of the previous
step) and substitute this for the mass of star A in the first step (Kepler's
3rd law step).
- You will find star B's mass = the total mass/(1 + the fraction from step
2).
- Star A's mass = star B's mass × (the fraction from step 2).
- Check that the proportions add up to the total mass!
(By the way,
you can use this proportion idea in cooking if you need to have a 32-ounce
mixture and the recipe calls for 3 parts sugar to 2 parts flour or if a recipe
is for 6 people but you need to serve 8 people.) The masses of different types
of stars are summarized in the Main
Sequence Star Properties table below.
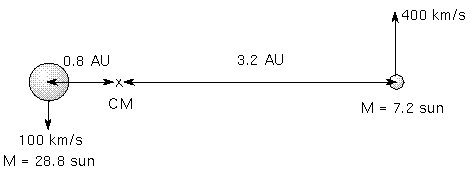
How do you do that?Use the observed velocities in the figure
below to find the individual masses of the stars. The stars have a
measured period of 4/3 years and a separation distance of 4 A.U.
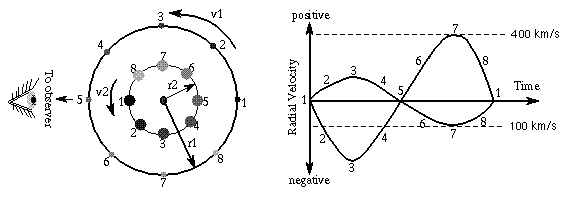
- Step 1:
- Kepler's third law says the total mass =
43/(4/3)2 = 64/(16/9) = 36 solar masses.
- Step 2:
- I will let the massive star be ``star A''. So (mass star A)/(mass
star B) = 400/100 = 4.
- Steps 3 and 4:
- mass star B = 36 solar masses/(1 + 4) = 7.2 solar masses.
- Step 5:
- mass star A = mass star B × 4 = 28.8 solar masses.
- Step 6: Check:
- 28.8 solar masses + 7.2 solar masses does equal 36 solar masses.
This step makes sure you did not make an arithmetic error in the
previous steps. If the sum does not equal the value in step 1, then
re-check your math!
 |
Vocabulary
| center of mass |
radial velocity curve |
spectroscopic binary |
Formulae
- Center of mass distance: mass star A / mass star B = distance B /
distance A, where the distances are each measured from the center of mass.
Notice which star's distance is in the top of the fraction!
- separation distance = distance A + distance B, where the distances are
each measured from the center of mass.
- Center of mass velocity: mass star A / mass star B = velocity star
B / velocity star A. Notice which star's velocity is in the top of the
fraction!
- Kepler's 3rd law: (mass star A + mass star B) = (separation
distance)3 / (orbital period)2 if use solar mass units,
A.U. for the distance unit between the stars, and the time unit of years for
the orbital period.
Review Questions
- How the masses of stars found? What kind of star systems are used and
which famous law of orbital motion is used?
- How many times closer to the center of mass is the massive star
than the low-mass star?
- How do you use the radial velocity curve to find the mass
proportions and separation distance? How much faster or slower does the
low-mass star move than the massive star?
- Three binary systems with a separation of 2 A.U. between the two stars in
each system. System (1) has the two stars orbiting the center of mass in 1
year, system (2) has the two stars orbiting the center of mass in 5 months,
and system (3) has the two stars orbiting the center of mass in 2 years. Put
the binary systems in the correct order by increasing total mass
(least massive first and ignore the inclination angle i).
- Star A is 0.2 A.U. from the center of mass and its companion star B is 0.6
A.U. from the center of mass. Which star is more massive?
- If the two stars in the previous question have orbital periods of 0.35777
years, what are the individual masses of the two stars? (Hint: find their
combined mass from Kepler's third law and then use their relative center of
mass distances to find how many times more massive one star is than the
other.)
- Use the radial velocity curve graph in the text above. Assume that star A
reaches a velocity of 90 kilometers/second and star B reaches only 10
kilometers/second. If the separation distance = 10 A.U., and the orbital
period = 10 years, what is the combined mass of the two stars? From the center
of mass relation also find (star A mass)/(star B mass) and their individual
masses.
- Which star system(s) would you be able to measure the radial velocity: (a)
stars orbiting in a plane that is along our line of sight (i=0°); (b)
stars orbiting in a plane that is perpendicular to our line of sight (face-on,
i=90°); (c) stars orbiting in a plane with i=30°.
The Sizes of Stars
Eclipsing binaries are used
to determine the diameters of stars. These are two stars orbiting each other in
a plane that is parallel to your line of sight so you see their orbits edge-on.
This means that one star will periodically cover up the other star. During the
eclipse the total brightness measured for the binary will decrease. The amount
of the dip in brightness depends on the luminosity and relative size of the two
stars.
A star's diameter is found from speed = (distance travelled)/(time it
takes). The speed comes from the doppler shift and the time is the length
of the eclipse. The distance travelled during the eclipse is equal to the
diameter of the star = 2 × radius. The light curve---plot of brightness
vs. time---is used to derive the star diameters. Here is an example of two stars
orbiting each other in circular orbits seen edge-on with one star small and hot
and the other large and cool:

When the small star moves from position 1 to position 2 (or from position 3
to position 4), it has moved a distance equal to its diameter. When the small
star moves from position 1 to position 3 (or from position 2 to position 4), it
has moved a distance equal to the diameter of the large star.
Star sizes can also be found (less accurately) from the luminosity and the
flux. Recall from the magnitude
section above that the luminosity = [4p×(star
radius)2] × [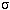 ×(star's surface temperature)4], where
×(star's surface temperature)4], where 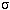 is the Stefan-Boltzmann
constant. If you compare the star with the Sun, you can cancel out the constants
to get (star's radius)/(Sun's radius) = (Sun's temperature/star's
temperature)2 × Sqrt[star's luminosity/Sun's luminosity].
See the ``How do you do that?'' box below for an example. The sizes of different
types of stars are summarized in the Main
Sequence Star Properties table below.
is the Stefan-Boltzmann
constant. If you compare the star with the Sun, you can cancel out the constants
to get (star's radius)/(Sun's radius) = (Sun's temperature/star's
temperature)2 × Sqrt[star's luminosity/Sun's luminosity].
See the ``How do you do that?'' box below for an example. The sizes of different
types of stars are summarized in the Main
Sequence Star Properties table below.
How do you do that?Antares is 9120 times more luminous than the
Sun (Antares' luminosity/Sun's luminosity)= 9120) and has a temperature of
only 3340 K and the Sun's temperature is 5840 K. Antares' size/Sun's size
= (5840/3340)2 × Sqrt[9120] = 3.057 × 95.5 = 292.
Antares is almost 300 times the size of the Sun! If the Sun were replaced
by Antares, the inner planets Mercury, Venus, and Earth would be
inside Antares! It is a red giant star---a star close to death.
|
Vocabulary
| light curve |
eclipsing binary |
Formulae
- Eclipsing binary: diameter = speed × time of eclipse.
- Size from luminosity: star's radius/Sun's radius = (Sun's
temperature/star's temperature)2 Sqrt[star's
luminosity/Sun's luminosity].
Review Questions
- How do you use the light curve to find the diameters of stars?
- What special type of binary star system is used to find the diameters of
stars?
- Use the light curve in the figure in the section above. Assume that when
star A is behind star B, the small dip in brightness is seen. When star B is
behind star A, the big dip in brightness is seen. Which star is more luminous?
- From the previous problem, if t1 = 45 minutes, t2 = 60 minutes, t3 = 105
minutes, t4 = 120 minutes, what is (star A diameter)/(star B diameter)? [Hint:
find which star is brighter and in this circular orbit system (t8 - t6) = (t4
- t2).]
- From the previous problem, if the velocity is 750 kilometers/second, what
is the diameter of the larger star?
- The white dwarf Sirius B has a temperature of 14,000 K and a luminosity
only 0.00794 times the Sun's luminosity. What is the diameter of
Sirius B in kilometers? (The Sun's radius = 696,000 kilometers.)
 Go
to Magnitude System section
Go
to Magnitude System section
 Go to
Stellar Types and HR diagram section
Go to
Stellar Types and HR diagram section
Go to Astronomy Notes beginning
last update: 02 March 1999
Is this page a copy of
Strobel's Astronomy Notes?
Author of original content:
Nick Strobel


![]() is a positive number. The spectral lines appear shifted to the red end of the
spectrum, so the shift is called a redshift. If the star is moving toward
you, then the wavelengths appear to the compressed and
is a positive number. The spectral lines appear shifted to the red end of the
spectrum, so the shift is called a redshift. If the star is moving toward
you, then the wavelengths appear to the compressed and ![]() is a negative number. The
spectral lines are shifted to the blue end of the spectrum, so the shift is
called a blueshift. The doppler effect tells you only about the motion
relative to you. If you move toward the star or it moves toward you,
the doppler effect will be the same. The Earth is in motion relative to the star
because it are orbiting the Sun, so you have to take the Earth's orbital motion
into account when figuring the star's velocity from the doppler effect.
is a negative number. The
spectral lines are shifted to the blue end of the spectrum, so the shift is
called a blueshift. The doppler effect tells you only about the motion
relative to you. If you move toward the star or it moves toward you,
the doppler effect will be the same. The Earth is in motion relative to the star
because it are orbiting the Sun, so you have to take the Earth's orbital motion
into account when figuring the star's velocity from the doppler effect.

![]() /dt). This is how many degrees on
the sky the star moves in a given amount of time and is called the proper
motion by astronomers. If you determine the star's distance from its
trigonometric parallax or the inverse square law method, you can convert the
angular velocity (proper motion) to tangential velocity in physical units such
as kilometers/second. The tangential velocity = k × the star's distance ×
the proper motion, where k is a conversion factor that will take care of
the conversion from arc seconds and parsecs and years to kilometers/second.
Using the Pythagorean theorem for right triangles, you find that the star's
total velocity = Sqrt[(radial velocity)2 + (tangential
velocity)2].
/dt). This is how many degrees on
the sky the star moves in a given amount of time and is called the proper
motion by astronomers. If you determine the star's distance from its
trigonometric parallax or the inverse square law method, you can convert the
angular velocity (proper motion) to tangential velocity in physical units such
as kilometers/second. The tangential velocity = k × the star's distance ×
the proper motion, where k is a conversion factor that will take care of
the conversion from arc seconds and parsecs and years to kilometers/second.
Using the Pythagorean theorem for right triangles, you find that the star's
total velocity = Sqrt[(radial velocity)2 + (tangential
velocity)2].








![]() ×(star's surface temperature)4], where
×(star's surface temperature)4], where ![]() is the Stefan-Boltzmann
constant. If you compare the star with the Sun, you can cancel out the constants
to get (star's radius)/(Sun's radius) = (Sun's temperature/star's
temperature)2 × Sqrt[star's luminosity/Sun's luminosity].
See the ``How do you do that?'' box below for an example. The sizes of different
types of stars are summarized in the Main
Sequence Star Properties table below.
is the Stefan-Boltzmann
constant. If you compare the star with the Sun, you can cancel out the constants
to get (star's radius)/(Sun's radius) = (Sun's temperature/star's
temperature)2 × Sqrt[star's luminosity/Sun's luminosity].
See the ``How do you do that?'' box below for an example. The sizes of different
types of stars are summarized in the Main
Sequence Star Properties table below.
![]() Go
to Magnitude System section
Go
to Magnitude System section ![]() Go to
Stellar Types and HR diagram section
Go to
Stellar Types and HR diagram section