Full window version (looks a little nicer). Click <Back>
button to get back to small framed version with content indexes.
This material (and images) is copyrighted!.
See my copyright
notice for fair use practices.
Now I will apply Newton's laws of motion and gravity to topics more
astronomical: objects moving around other objects. What kinds of things can you
find out about celestial objects from just observing their motions?
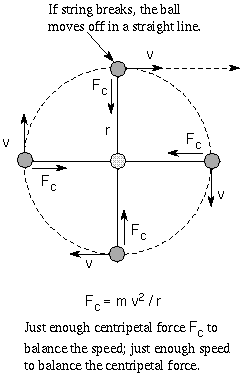Newton's first law of motion says that an object's inertia will keep
it from changing its speed and/or direction unless some force acts on it. This
means that satellites orbiting the Earth must be feeling some force that
constantly deflects them toward the center of the Earth. If there was no force,
they would travel in a straight line at a constant speed.
If you whirl a ball attached to string around your head, it moves in a
circular path around you because the string is always pulling the ball directly
toward the hand grabbing the string. The ball wants to move in a straight line
and the string is pulling it directly inward. The resulting deflection is a
compromise: a circular path. The string is applying a centripetal force
to the ball: an inward force. If you let go of the string, there is no
centripetal force and the ball will fly off in a straight line because
of its inertia. If you do not whirl the ball fast enough it will move inward to
a smaller non-circular path around you. If you whirl the ball too fast, you may
not be able to give it enough centripetal force to keep it in a circular path
around you. The amount of centripetal force needed to balance an object's
inertia and keep it in a circular path of radius r is found from Newton's
second law: the centripetal force = m v2 / r, where v
and m are the object's speed and mass, respectively. The radius of the
orbit r is the same as the distance between the moving object and the
central body.
Now for orbits!
Satellites are not being deflected by strings but by gravity. Gravity provides
the centripetal force needed to keep the satellites in orbit. If you focus on
the simple case of circular orbits, you can use the centripetal force formula
above with the law of gravity to determine the mass of a planet or star. Simply
set the force of gravity equal to the centripetal force and solve for the mass
of the planet or star, M.
The satellite mass m cancels out
from both sides and if you put M on one side and the rest on the other
side of the equation, you get
This assumes that the
satellite's mass, m, is much less than the central object's mass so you
can ignore the acceleration of the central object toward the satellite!
How do you do that?Let's use this result to get an estimate of
the mass of the Sun. You need to use something orbiting with a known
radius and speed. The Earth's orbit is roughly circular with radius = 1.5
× 1011 meters and the Earth moves with a speed 30,000
meters/second (= 30 km/s) in its orbit. The distance is given in meters to
match the units of the speed. The distance unit of a meter is used because
you will be using the gravitational constant G in your calculation
and it uses the meter unit. When you do a calculation, you must be sure
you check that your units match up or you will get nonsense answers.
Plug the values into the mass relation:
the Sun's mass =
(30,000)2 × (1.5 × 1011)/(6.7 × 10-11) =
2 × 1030 kilograms. This is much larger than the Earth's mass
so it was okay to ignore the Sun's movement toward the Earth. Using no
approximations (ie., not assuming a circular orbit and including the Sun's
motion toward the Earth) gives a value for the Sun's mass that is very
close to this. Your answer does not depend on which planet you choose to
use (here you used the Earth's orbit). You would get the same value for
the mass of the Sun if you had used any of the other planets orbital
speeds and sizes. |
This relation tells you what you need to know in order to measure a planet's
or star's mass: the orbital speed of a satellite and the distance it is from the
center of the planet or star. Because the velocity is on top of the fraction,
satellites are made to move faster if the mass of the central object is greater.
At the same distance, a massive planet will exert more gravity force than a
low-mass planet, so the massive planet will produce greater inward accelerations
on satellites orbiting it. The satellites will, therefore, orbit at faster
speeds.
Sometimes the orbital period P is measured instead of the orbital
velocity. The orbital period is the time it takes the object to travel the
circumference of its orbit (for a circle, the circumference = 2pr, where p is approximately
3.1416). Recall that speed = (distance travelled)/time, so the speed v =
the circumference of the orbit/orbital period. When you substitute this for the
speed in the mass relation above, you get
This
may look familiar to you---it is Kepler's third law! There is a distance cubed,
an orbital period squared, and some other contant factors. Newton found that
when Kepler used the motions of the planets to formulate his third law, Kepler
was actually measuring the mass of the Sun. If you use the convenient set of
units of an astronomical unit for the distance, a year for the time, and a
``solar mass'' (mass relative to the Sun) for the mass, the complicated term
(4p2)/G becomes the simple value of
1. For the planets orbiting the Sun, the mass relation becomes 1 =
r3 / P2, or r3 =
P2, just what Kepler found.
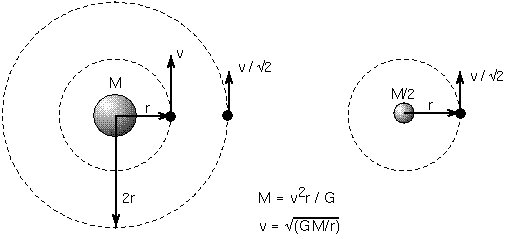The mass formula above tells you that
satellites orbiting massive planets must move faster than satellites orbiting
low-mass planets at the same distance. Massive planets have stronger gravity
than low-mass planets so a satellite orbiting a massive planet is accelerated by
a greater amount than one going around a lesser mass planet at the same
distance. To balance the stronger inward gravitational pull of the massive
planet, the satellite must move faster in its orbit than if it was orbiting a
lesser mass planet. Of course, this also applies to planets orbiting stars,
stars orbiting other stars, etc.
If you solve for the orbit speed, v, in the mass formula, you can find
how fast something needs to move to balance the inward pull of gravity:
v2 = (G M)/r . Taking the square root of both
sides (you want just v not v2), you get
v = Sqrt[(G M)/r].
How do you do that?Find the orbital speed of Jupiter around the
Sun. Jupiter's distance from the Sun is 5.2 A.U., or 7.8×1011
meters and the Sun's mass is 2×1030 kilograms. The orbital
speed of Jupiter around the Sun is Sqrt[6.7×10-11 ×
(2×1030)/(7.8×1011)] =
Sqrt[1.718×108] = 1.3×104 meters/second, or
13 kilometers/second. What do you think you wouldd find if you used one of
the Trojan asteroids, millions of times less massive than Jupiter, that
orbits the Sun at 5.2 A.U.? |
If an object moves fast enough it can
escape a massive object's gravity and not be drawn back toward the massive
object. The critical speed needed to do this is the escape velocity. More
specifically, this is the initial speed something needs to escape the
object's gravity and assumes that there is no other force acting on the object
besides gravity after the initial boost. Rockets leaving the Earth do not have
the escape velocity at the beginning but the engines provide thrust for an
extended period of time, so the rockets can eventually escape. The concept of
escape velocity applies to anything gravitationally attracted to anything else
(gas particles in planet atmospheres, comets orbiting the Sun, light trying to
escape from black holes, galaxies orbiting each other, etc.).
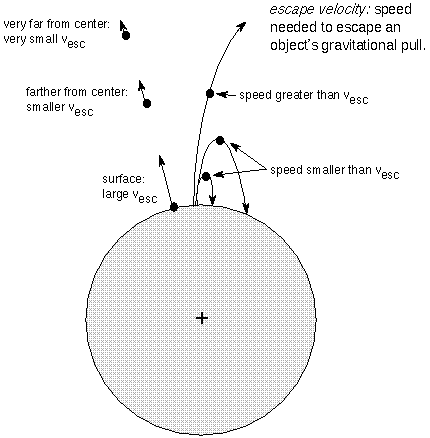
Using Newton's laws of motion and law of gravity, you can find that the
escape velocity vesc looks very similar to the orbital speed:
vesc = Sqrt[(2 G M)/r]. This is
a factor
Sqrt[2] larger than the circular orbital
speed. Since the mass M is on top of the fraction, the escape
velocity increases as the mass increases. More massive bodies exert greater
gravity force, so escaping objects have to move faster to overcome the greater
gravity. Also, the distance from the center of the object r is in the
bottom of the fraction, so the escape velocity DEcreases as the distance
increases. Gravity decreases with greater distance, so objects farther from a
massive body do not need to move as quickly to escape it than those closer to
it.
How do you do that?Find the escape velocity from the surface of
the Earth. Using
the acceleration of gravity, you can find that the Earth has a mass of
6.0×1024 kilograms. The Earth's radius is 6.4×106
meters. Since the mass and distance from the center are in the standard
units, you just need to plug their values into the escape velocity
relation.
The Earth's surface escape velocity is Sqrt[2×
(6.7×10-11) × (6.0×1024)/ (6.4×106)] =
Sqrt[1.256×108] = 1.1×104 meters/second (= 11
km/s). Here are some other surface escape velocities: Moon = 2.4 km/s,
Jupiter = 59.6 km/s, Sun = 618 km/s. |
Vocabulary
| centripetal force |
escape velocity |
Formulae
- Mass of central object = [(orbital speed)2 ×
distance)/G.
- Mass of central object (Kepler's 3rd law) = (4p2)/G × [(distance)3/(orbital
period)2].
- Orbital speed = Sqrt[G × Mass / distance].
- Escape velocity = Sqrt[2G × Mass / distance].
- What keeps satellites orbiting the Earth moving along their curved paths?
- What two things must be determined first in order to calculate the mass of
a planet or a star?
- Jupiter's moon Io has about the same mass as the Moon and orbits Jupiter
at about the same distance that the Moon orbits the Earth (center to center).
Then why does Io take only 1.8 days to orbit Jupiter but our Moon takes 27.3
days to orbit the Earth?
- Astronomers were able to accurately measure the orbital periods of the
moons of Jupiter since the time of Galileo, so why was an accurate value for
Jupiter's mass not found for over 300 years until the astronomical unit was
measured accurately?
- Which would have a shorter orbital period, a planet orbiting a massive
star at 3 A.U. or a planet orbiting a low-mass star at 3 A.U.? Explain your
answer.
- If a planet orbiting a massive star has the same orbital period as a
planet orbiting a low-mass star, which of the planets orbits at a greater
distance from its star? Explain your answer.
- What two things does the escape velocity depend on?
- Why does the planet Saturn with over 95 times the Earth's mass have a
smaller escape velocity at its cloudtops than the Earth has at its
cloudtops?
- Why is Jupiter's escape velocity at its cloudtops over two times
higher than the Earth's surface escape velocity, even though Jupiter
has a much larger diameter than the Earth?
Kepler's third law of planetary motion
says that the average distance of a planet from the Sun cubed is
directly proportional to the orbital period squared. Newton found that
his gravity force law could explain Kepler's laws. Since Newton's law of gravity
applies to any object with mass, Kepler's laws can be used for any object
orbiting another object. Let's look at satellites orbiting a planet.
If you have two satellites (#1 and #2) orbiting a planet, Kepler's third law
says:
(period #1/period #2)2 = (distance #1/distance
#2)3, where the distance is the average distance of the
satellite from the planet---the orbit's semimajor axis. The satellites must be
orbiting the same planet in order to use Kepler's third law! Kepler found this
law worked for the planets because they all orbit the same star (the Sun).
If you have measured the orbital period of one satellite around a planet, you
can then easily find how long it would take any other satellite to orbit the
planet in any size oribt. Kepler's third law can be simplified down to
| period #1 |
= |
period #2 × Sqrt[(distance #1/distance #2)3] |
|
OR |
|
| period #1 |
= |
period #2 × (distance #1/distance
#2)3/2. |
Those of you with a scientific calculator (one that does powers, trig
functions, scientific notation, etc.) will want to use the formula on the last
line (remember that 3/2 = 1.5). Those with a calculator that just has a square
root button will want to use the formula on the second-to-last line.
If the satellite is orbiting the Sun, then the relation can be greatly
simplified with an appropriate choice of units: the unit of years for
the orbit period and the distance unit of astronomical units. In this
case, the reference ``satellite'' is the Earth and Kepler's third law becomes
period = distance3/2. Let's use this to find out how long it takes to
explore the solar system.
The simplest way to travel between
the planets is to let the Sun's gravity do the work and take advantage of
Kepler's laws of orbital motion. A fuel efficient way to travel is to put the
spacecraft in orbit around the Sun with the Earth at one end of the orbit at
launch and the other planet at the opposite end at arrival. These orbits are
called ``Hohmann orbits'' after Walter Hohmann who developed the theory for
transfer orbits. The spacecraft requires only an acceleration at the beginning
of the trip and a deceleration at the end of the trip to put it in orbit around
the other planet.
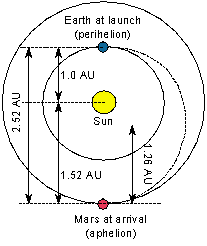Let's go to Mars! The
relative positions of Earth and Mars must be just right at launch so that Mars
will be at the right position to greet the spacecraft when it arrives several
months later. These good positionings happen once every 780 days (the synodic
period of Mars). The spacecraft must be launched within a time interval called
the ``launch window'' that is just few of weeks long to use a Hohmann orbit for
the spacecraft's path. The Earth is at the perihelion (point closest to
the Sun) of the spacecraft orbit (here, 1.0 A.U.) and Mars is at the
aphelion (point farthest from the Sun---here, 1.52 A.U.).
Kepler's third law relates the semi-major axis of the orbit to its sidereal
period. The major axis is the total length of the long axis of the elliptical
orbit (from perihelion to aphelion). For the Mars journey, the major axis = 1.52
+ 1.0 A.U. = 2.52 A.U. The semi-major axis is one-half of the major
axis, so divide the major axis by two: 2.52/2 = 1.26 A.U. Now apply
Kepler's third law to find the orbital period of the spacecraft =
1.263/2 = 1.41 years. This is the period for a full orbit (Earth to
Mars and back to Earth), but you want to go only half-way (just Earth to Mars).
Travelling from Earth to Mars along this path will take (1.41 / 2) years = 0.71
years or about 8.5 months.
When the craft is launched, it already has the Earth's orbital velocity of
about 30 km/sec. Since this is the speed for a circular orbit around the Sun at
1.0 A.U., a reduction in the spacecraft's speed would make it fall closer to the
Sun and the Hohmann would be inside the Earth's orbit. Since you want
to go beyond the Earth's orbit, the spacecraft needs an increase in its speed to
put it in an orbit that is outside the Earth's orbit. It will slow down
gradually as it nears aphelion.
At aphelion the spacecraft will not be travelling fast enough to be in a
circular orbit at Mars' distance (1.52 A.U.) so it will need to arrive at
aphelion slightly before Mars does. Mars will then catch up to it. But
the spacecraft will be moving much too fast to be in a circular orbit around
Mars, so it will need to slow down to go in orbit around Mars.
On its journey to Mars, the spacecraft's distance from the Sun is
continuously monitored to be sure the craft is on the correct orbit. Though the
spacecraft responds mostly to the Sun's gravity, the nine planets' gravitational
pulls on the spacecraft can affect the spacecraft's path as it travels to Mars,
so occasional minor firings of on-board thrusters may be required to keep the
craft exactly on track.
Vocabulary
Formulae
- Kepler's third law: period #1 = period #2 × Sqrt[(distance
#1/distance #2)3]
- Kepler's third law: period #1 = period #2 × (distance #1/distance
#2)3/2
- If considering objects orbiting the Sun, measure the orbit period in
years and the distance in A.U. With these units, Kepler's
third law is simply: period = distance3/2.
- How can you predict the orbital period of Jupiter's satellite Europa from
observations of the other jovian moon Io?
- If Io takes 1.8 days to orbit Jupiter at a distance of 422,000 kilometers
from its center, find out how long it would take Europa to orbit Jupiter at
671,000 kilometers from its center.
- If the Moon were twice as far from the Earth as it is now, how long could
a solar eclipse last? (Solar eclipses currently last up to about two hours
from the start of the cover-up to when the Moon no longer blocks the Sun at
all.)
- The Hubble Space Telescope orbits the Earth 220 kilometers above the
surface and takes about 1.5 hours to complete one orbit. How can you find out
how far up to put a communication satellite, so that it takes 24 hours to
circle the Earth? (Such an orbit is called a ``geosychronous orbit'' because
the satellite remains above a fixed point on the Earth.)
- Why does NASA not launch interplanetary spacecraft when the planets are at
opposition (closest to the Earth)?
- Find out how long it will take the Cassini spacecraft to travel to Saturn
9.5 A.U. from the Sun.
When you look in the paper at the section
containing the tide tables, you will often see the phase of the moon indicated
as well. That is because the ocean tides are caused by different strengths of
the Moon's gravity at different points on the Earth. The side of the Earth
facing the Moon is about 6400 kilometers closer to the Moon than the center of
the Earth is, and the Moon's gravity pulls on the near side of the Earth more
strongly than on the Earth's center. This produces a tidal bulge on the side of
the Earth facing the Moon. The Earth rock is not perfectly rigid; the side
facing the Moon responds by rising toward the Moon by a few centimeters on the
near side. The more fluid seawater responds by flowing into a bulge on the side
of the Earth facing the Moon. That bulge is the high tide.
At the same time the Moon exerts an attractive force on the Earth's center
that is stronger than that exerted on the side away from the Moon. The Moon
pulls the Earth away from the oceans on the far side, which flow into a bulge on
the far side, producing a second high tide on the far side.
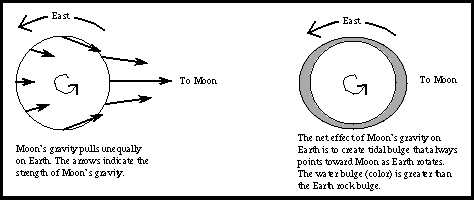
These tidal bulges are always along the Earth-Moon line and the Earth rotates
beneath the tidal bulge. When the part of the Earth where you are located sweeps
under the bulges, you experience a high tide; when it passes under one of the
depressions, you experience a low tide. An ideal coast should experience the
rise and fall of the tides twice a day. In reality, the tidal cycle also depends
on the latitude of the site, the shape of the shore, winds, etc.
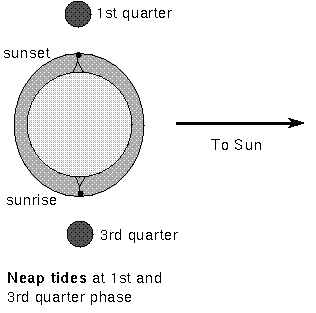
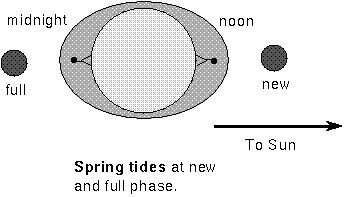
The Sun's gravity also produces tides that are about half as strong as the
Moon's and produces its own pair of tidal bulges. They combine with the lunar
tides. At new and full moon, the Sun and Moon produce tidal bulges that add
together to produce extreme tides. These are called spring tides (the
waters really spring up!). When the Moon and Sun are at right angles to each
other (1st & 3rd quarter), the solar tides reduce the lunar tides and you
have neap tides.
As the Earth rotates beneath
the tidal bulges, it attempts to drag the bulges along with it. A large amount
of friction is produced which slows down the Earth's spin. The day has been
getting longer and longer by about 0.0016 seconds each century.
Over the course of time this friction can have a noticeable effect.
Astronomers trying to compare ancient solar eclipse records with their
predictions found that they were off by a significant amount. But when they took
the slowing down of the Earth's rotation into account, their predictions agreed
with the solar eclipse records. Also, growth rings in ancient corals about 400
hundred million years old show that the day was only 22 hours long so that there
were over 400 days in a year. In July 1996 a research study reported evidence,
from several sedimentary rock records providing an indicator of tidal periods,
that the day was only 18 hours long 900 million years ago.
Eventually the Earth's rotation will slow down to where it keeps only one
face toward the Moon. Gravity acts both ways so the Earth has been creating
tidal bulges on the Moon and has slowed it's rotation down so much that it
rotates once every orbital period. The Moon keeps one face always toward the
Earth.
Here is a list of references about the evidence for the
slowing down of the Earth's rotation:
- Growth Rhythms and the History of the Earth's rotation, edited by
G.D. Rosenberg and S.K. Runcorn (Wiley: New York, 1975). An excellent source
on the eclipse records and the biology of coral and their use as chronometers.
- Tidal Friction and the Earth's Rotation, edited by P. Brosche and
J. Sündermann (Springer Verlag, 1978). The second volume put out in 1982 does
not talk about eclipse records or the use of coral but, instead, goes into the
astrophysics of the Earth-Moon dynamics and geophysics of internal Earth
processes effects on the Earth's rotation.
- Earth's Rotation from Eons to Days, edited by P. Brosche and J.
Sündermann (Springer Verlag, 1990). Has several articles about the use of
ancient Chinese observations.
- Richard Monastersky 1994, Ancient tidal fossils unlock lunar
secrets in Science News vol. 146, no. 11, p. 165 of the 10 Sept
1994 issue.
- C. P. Sonett, E. P. Kvale, A. Zakharian, Marjorie A. Chan, T. M. Demko
1996, Late
Proterozoic and Paleozoic Tides, Retreat of the Moon, and Rotation of the
Earth in Science vol 273, no. 5271, p. 100 of the 05 July 1996
issue.
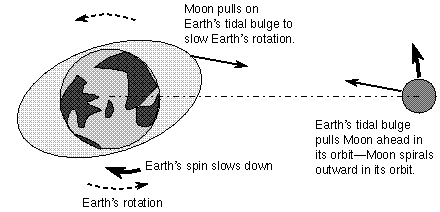Friction with the ocean beds
drags the tidal bulges eastward out of a direct Earth-Moon line and since these
bulges contain a lot of mass, their gravity pulls the moon forward in its orbit.
The increase in speed enlarges the Moon's orbit. Currently, the Moon's
distance from the Earth is increasing by about 3 centimeters per year.
Astronomers have been able to measure this slow spiralling out of the Moon by
bouncing laser beams off reflectors left by the Apollo astronauts on the lunar
surface.
The consequence of the Moon's recession from the Earth because of the slowing
down of the Earth's rotation is also an example of the conservation of
angular momentum. Angular momentum is the amount of spin motion an object or
group of objects has. It depends on the geometric size of the object or group of
objects, how fast the object (or group of objects) is moving, and the mass of
the object (or the group). Since the Earth's angular momentum is decreasing, the
Moon's angular momentum must increase to keep the overall angular
momentum of the Earth-Moon system the same. The concept of angular momentum is
discussed further in the Angular
Momentum appendix.
The slow spiralling out of the Moon means that there will come a time in the
future when the angular size of the Moon will be smaller than the Sun's and we
will not have any more total solar eclipses! Fifty billion years in the future
the Earth day will equal 47 of our current days and the Moon will take 47 of our
current days to orbit the Earth. Both will be locked with only one side facing
the other---people on one side of the Earth will always see the Moon while
people on the other side will only have legends about the Moon that left their
pleasant sky.
Of course, one should bear in mind that the Sun itself is only likely to live
for another 5 billion years.
Tidal effects are larger for
more massive objects and at closer distances. The Sun produces a tidal bulge on
the planet Mercury (the planet closest to the Sun) and has slowed that planet's
rotation period so it rotates three times for every two times it orbits the Sun
(a ``3 - 2 spin-orbit resonance''). Jupiter's moon, Io, orbits at about the same
distance from Jupiter's center as the Earth's moon. Jupiter is much more massive
than the Earth, so Jupiter's tidal effect on Io is much greater than the Earth's
tidal effect on the Moon. Io is stretched by varying amounts as it orbits
Jupiter in its elliptical orbit. This tidal flexing of the rock material creates
huge amounts of heat from friction in Io's interior which in turn is released in
many volcanic eruptions seen on Io. Galaxies passing close to each other can be
severely stretched and sometimes pulled apart by mutual tidal effects.
Vocabulary
| conservation of angular momentum |
neap tide |
spring tide |
- What causes the tides?
- How are tides related to the position of the Moon and Sun with respect to
the Earth?
- Why are there two high tides roughly every 12.5 hours? Explain
why there are two tidal bulges AND why they are over 12 hours apart.
- At what phases do spring tides occur?
- At what phases do neap tides occur?
- How are tides responsible for the slowing down of the Earth's spin and the
Moon's spiralling away from us?
- Where are some other places that tides play a significant role in the
appearance and motion of objects?
Go
to Gravity Introduction section
last updated 25 January 1999
Is this page a copy of
Strobel's Astronomy Notes?
Author of original content:
Nick Strobel
