Here, as noted above, our definition of ![]() becomes
arbitrary. However, by a change of variables to
becomes
arbitrary. However, by a change of variables to
|
x = |
(9) |
t = 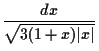
|
(10) |
Examination of the general solution (Eq. 4)
shows that for very large ![]() ,
k becomes irrelevant: if r is small enough that the term
in
,
k becomes irrelevant: if r is small enough that the term
in ![]() becomes comparable to unity, then 3kr
becomes comparable to unity, then 3kr ![]() 1, whereas
if 3kr > 1 then the term in
1, whereas
if 3kr > 1 then the term in ![]() dominates. Thus these cases
are actually equivalent to the cases where
dominates. Thus these cases
are actually equivalent to the cases where
![]() = ±
= ±![]() .
.
This is a similar situation to the previous one: there are two functional forms, depending on the sign of k. For k = + 1 there is the `cycloid' universe
|
|
(11) |
|
|
(12) |
This corresponds to just one universe, the Einstein-de Sitter case. This is a scale-free solution, i.e. there is no characteristic time or size; instead the density is a unique function of time (or vice versa); our integral solution reduces to
t = 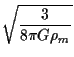 = = |
(13) |
There are also six special cases when the matter density is strictly zero.
There is a trivial empty static universe when k = 0 and
![]() = 0,
in which case H = 0. This can be thought of as the limit of the
Einstein-de Sitter universe when
t
= 0,
in which case H = 0. This can be thought of as the limit of the
Einstein-de Sitter universe when
t ![]()
![]() .
.
Next is the Milne solution,
when
![]() = 0 and k = - 1 (to make H2 positive) and hence
= 0 and k = - 1 (to make H2 positive) and hence
| R = ct. | (14) |
In the de Sitter solution k = 0 and
![]() > 0. The Hubble parameter is then constant at
> 0. The Hubble parameter is then constant at
|
H2 = |
(15) |
|
t = |
(16) |
The other three cases correspond to both ![]() and k non-zero:
note that for M* = 0,
and k non-zero:
note that for M* = 0,
![]()
![]() 0, k = + 1, is ruled out because it
would give a negative H2 (similarly
0, k = + 1, is ruled out because it
would give a negative H2 (similarly
![]() < 0, k = 0).
For all these R
< 0, k = 0).
For all these R![]() sets the absolute
scale, and there are no continuous parameters that affect the shape.
sets the absolute
scale, and there are no continuous parameters that affect the shape.
To summarize the M* = 0 cases:
| k | Rturn | Type | |
| < 0 | -1 |
(- 3 |
Bang-crunch. |
| 0 | 0 | - | Static |
| 0 | -1 | - | Milne: Linear Expansion |
| > 0 | -1 | - | Continuous expansion |
| > 0 | 0 | 0 | de Sitter: Exponential expansion |
| > 0 | +1 |
(3 |
Bounce |