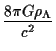
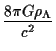
In fact there are two characteristic lengths in the problem, determined
by M* and ![]() respectively:
respectively:
Rm = 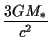 ; R ; R |
(1) |
We will use Rm to define scaled versions of radius and time:
|
r = R/Rm; |
(2) |
The cosmological constant has dimensions inverse area, so we can make it dimensionless by defining
|
|
(3) |
Using these parameters the solution of the Friedman equation can be written
The lower limit of the integral, r0 , is the radius at our chosen t = 0; it makes sense to choose this as the time when r is a minimum, usually zero.Typically the integral only exists over a finite range of r, limited by the denominator becoming zero. These limiting sizes correspond to turnarounds (if there is an upper limit to r) or bounces (for lower limits). After turnaround the size evolution reverses, corresponding to taking the negative square root; similarly before the bounce (and so at negative times with t = 0 defined as suggested above).
As promised, the only continuous parameter that affects the shape of the
![]() (r) curve is
(r) curve is ![]() . Rm only affects the
overall scaling. In addition, of course, there are the
three possibilities for k. Note that
. Rm only affects the
overall scaling. In addition, of course, there are the
three possibilities for k. Note that ![]() , k and
Rm are constant throughout the history of each universe;
in particular
, k and
Rm are constant throughout the history of each universe;
in particular ![]() is constant along each track in the
is constant along each track in the
![]() -
-
![]() plane.
plane.
![]() parameterizes how important the cosmological constant is when the
universe has size of order Rm. For
parameterizes how important the cosmological constant is when the
universe has size of order Rm. For
![]()
![]() 1 and k = - 1,
there is a range of scales between Rm and R
1 and k = - 1,
there is a range of scales between Rm and R![]() when neither gravity
nor cosmological constant have much effect, and the universe expands
linearly, close to the Milne solution (see below). If
k = + 1 and
when neither gravity
nor cosmological constant have much effect, and the universe expands
linearly, close to the Milne solution (see below). If
k = + 1 and
![]()
![]() 1, the universe recollapses under gravity
before it ever reaches size R
1, the universe recollapses under gravity
before it ever reaches size R![]() , and the cosmological constant
has little effect. For
, and the cosmological constant
has little effect. For
![]()
![]() 1,
the cosmological constant takes over while the universe is still in its
initial Einstein-de Sitter phase (see below), and the scale Rm is
no longer important. If
1,
the cosmological constant takes over while the universe is still in its
initial Einstein-de Sitter phase (see below), and the scale Rm is
no longer important. If
![]()
![]() 1 and k = + 1, gravity and
cosmological repulsion nearly balance as r approaches unity: eventually
the universe either turns around to recollapse or begins to expand
exponentially, but the times for this to occur can be much longer than
either Rm/c or
R
1 and k = + 1, gravity and
cosmological repulsion nearly balance as r approaches unity: eventually
the universe either turns around to recollapse or begins to expand
exponentially, but the times for this to occur can be much longer than
either Rm/c or
R![]() /c.
/c.
If
0 < ![]() < 1 and k = + 1, the integral
solution is valid for two separate ranges of r:
from zero to a turnaround radius which ranges from 2/3 (when
< 1 and k = + 1, the integral
solution is valid for two separate ranges of r:
from zero to a turnaround radius which ranges from 2/3 (when
![]() = 0)
to 1 (when
= 0)
to 1 (when
![]() = 1); and from a bounce radius to infinity.
= 1); and from a bounce radius to infinity.
![]() = 1 is the loitering case, when the bounce radius is coincident
with the turnaround radius; otherwise it is larger. Thus the
two distinct regions of the
= 1 is the loitering case, when the bounce radius is coincident
with the turnaround radius; otherwise it is larger. Thus the
two distinct regions of the ![]() -
-
![]() plot with positive
plot with positive
![]() and k = + 1, which are outside the loitering trajectory,
correspond to these two branches of the solution for
the same values of
and k = + 1, which are outside the loitering trajectory,
correspond to these two branches of the solution for
the same values of ![]() .
.
The solutions for positive,
negative and zero ![]() have rather different properties;
furthermore, there are the two branches for
0 <
have rather different properties;
furthermore, there are the two branches for
0 < ![]() < 1, k = + 1.
This seems to give ten different
families of solutions; however we will see that cases with k or
< 1, k = + 1.
This seems to give ten different
families of solutions; however we will see that cases with k or
![]() zero are actually single solutions, not families, and they can
be treated as special cases of the five main families: furthermore we
will find a way to continuously link the families with k = - 1 and +1,
so that really there are only three families of curves to worry about,
i.e. the bang-crunch solutions, the bounce solutions, and the continuous
expansion solutions.
zero are actually single solutions, not families, and they can
be treated as special cases of the five main families: furthermore we
will find a way to continuously link the families with k = - 1 and +1,
so that really there are only three families of curves to worry about,
i.e. the bang-crunch solutions, the bounce solutions, and the continuous
expansion solutions.
In terms of the more familiar cosmological parameters, using
| r | = | 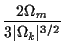 |
(5) |
| Rm | = | 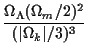 |
(6) |
|
|
(7) |
H2 = 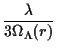 = = |
(8) |