Full window version (looks a little nicer). Click <Back>
button to get back to small framed version with content indexes.
This material (including line-art images and animations) is copyrighted!
See my copyright
notice for fair use practices.
The Sun produces a lot of light every second and it has been doing that for
billions of years. How does it or any other star produce so much energy for so
long? This section will cover how stars produce their energy. Astronomers have
known for a long time that the Sun produces a tremendous amount of energy. The
first part of this section will try to give you an idea of how much energy it
produces. Don't feel bad if you have trouble grasping the amount. It is
mind-boggling! There are several ways to generate the amount of energy coming
from the Sun. What distinguishes the correct explanation from the other models
is how long it can power the Sun.
The first basic
question about the Sun is how bright is it? It puts out A LOT of energy every
second. How much? The answer from our measurements is 4 × 1026 watts.
Such a large number is beyond most of our comprehension, so let's put the Sun's
total energy output (ie., its luminosity) in more familiar units. It is
equal to 8 #215; 1016 of the largest power plants (nuclear or
hydroelectric) on the Earth. Our largest power plants now can produce around
5,000 Megawatts of power. Another way to look at this is that the sun puts out
every second the same amount of energy as 2.5 × 109 of those
large power plants would put out every year---that's over two billion!
What could produce that much
energy every second? Let's first rule out other likely candidates. How about
chemical reactions? The most efficient chemical reaction is combining two
hydrogen atoms and one oxygen atom to make a water molecule plus some energy.
Such a reaction has a very small ``efficiency'' (something like 1/66000000 of
one percent). The efficiency = amount of energy released/(mass×
c2), where ``mass'' is the total mass of all of the atoms
involved and c is the speed of light. The amount of energy the Sun has
stored = the efficiency × (the mass of the fuel source) × c2.
To find out how long the Sun would last, you need to find out how much energy
the Sun has stored in its account and know how fast it makes withdrawals on its
account. The amount of time it would last is the amount of energy stored divided
by the rate of withdrawal: lifetime = energy stored/consumption rate = E
stored/Luminosity. Makes sense, yes? If the Sun could use all of its
hydrogen to make water, the chemical reactions would only power the Sun for
about 18,000 years. However, the amount of oxygen is much less than the
hydrogen, so the chemical reactions can power the Sun for only 30 years.
We need a reaction with a higher efficiency. How about the ultimate in
efficiency---a complete matter to energy conversion with 100% efficiency. Such a
reaction could power the Sun for 1013 years. Unfortunately, there are
problems with this because the number of heavy particles (protons + neutrons) in
the Sun must stay the same and protons are extremely stable---they don't
spontaneously change into energy (photons).
How about gravitational settling? This is a fancy way of
referring to the converting of the potential energy of the falling layers to
kinetic energy. When you hold a rock above the ground it has stored energy
(``potential energy''--it has the potential to do some work). The stored energy
is released as you let it fall. The rock gets kinetic energy because it is
moving. Kinetic energy can heat things up. This is what would happen to the
layers of the Sun if they were to fall inward toward the center of the Sun. The
gas would be compressed and, therefore, would heat up. In addition to the
expected heating, the gas would also radiate light.
Until the beginning of this century, this was the idea physicists strongly
argued for. This gravitational energy (with an efficiency of 1/10000 of one
percent) could power the sun for 30 million years---a nice long time except for
the nagging but ever louder criticism of the biologists who needed more time for
evolution to occur and the geologists who preferred the idea of an unlimited age
for the Earth but would stomach something like a few billion years for the age
of the Earth. A good article on the age-of-the-Earth debate is in Scientific
American August 1989 pages 90 to 96. Eventually, physicists had to change
their minds about the age of the Sun (and Earth) as radioactive dating indicated
a 4.6 billion year age for the solar system and, therefore, the Sun. It
was the fact that the Sun could not last long enough being powered by
gravitational contraction that motivated the search for nuclear power sources.
Nuclear power is the only thing left to power the Sun for as
long as it has been shining. There are two types possible: fusion and fission.
They both transform the nucleus of an atom into another type of
nucleus. Fission produces energy by breaking up massive nuclei
like uranium into less massive nuclei like helium and lead. Fusion
produces energy by fusing together light nuclei like hydrogen to make
more massive muclei like helium. Atomic power plants and the Atom Bomb use
fission to get the energy. Stars and Hydrogen bombs use fusion.
To get the positively-charged nuclei to fuse together, their electrical
repulsion must be overcome (remember that like charges repel and opposite
charges attract---something that rarely happens in human interactions). Once the
positively-charged nuclei are close enough together (within several
10-13 centimeters of each other), another fundamental force of nature
called the strong nuclear force takes over. It is much more powerful
than the electric force and makes the nuclei stick together.
To get those nuclei close enough together requires high temperatures
and high densities. At high temperatures the nuclei move fast enough to
be driven close enough together for them to fuse. The high densities ensure that
there are enough nuclei confined in a small volume for the collisions to take
place at all. The only place these extreme conditions occur naturally is in the
cores of stars.
The temperatures in the cores of stars are above the approximately 8 million
K needed to fuse hydrogen nuclei together. The amount of repulsion is larger for
nuclei with more positive charge so the fusion of elements with greater positive
charge requires greater temperatures and densities than that needed for fusing
elements with small positive charge. This is why stars fuse hydrogen nuclei
before they fuse other nuclei. For example, the fusion of helium nuclei requires
temperatures above 100 million K and heavier nuclei require even higher
temperatures. You will see in the next
chapter that these ultra-extreme conditions occur in the final stages of a
star's life cycle after the main sequence stage.
Fusion involves low-mass nuclei whose combined mass is
more than the resulting fused massive nucleus. The mass that was given
up to form the massive nucleus was converted to energy. Remember
E=mc2? That tells you how much energy (E) can be made
from matter with mass m. Remember that c is the speed of light and
it's squared (!) so a little bit of mass can make a lot of energy.
In the cores of main sequence stars, four hydrogen nuclei, each with the mass
of one proton, are fused together to form a single helium nucleus (two protons
and two neutrons) that has a mass of 3.97 times the mass of one proton. An
amount of mass equal to 0.03 times the mass of one proton was given up and
converted to energy equal to 0.03 × (mass one proton) × c2.
The efficiency of this reaction is about 4/5 of one percent. The Sun could last
for about 10 billion years on hydrogen fusion in its core. This is plenty long
enough to satisfy the modern geologists.
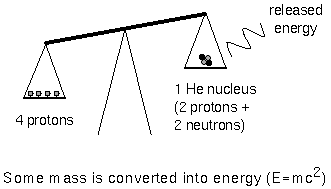The fusion
process in stars is a little more complicated than what was described above.
Rather than creating the helium nucleus in a single reaction, nature uses a
series of reactions to build up the helium nucleus step-by-step. In most stars a
three-step chain reaction is used called the ``proton-proton chain''. It is
described in the animation below. Massive stars also use a reaction that uses
carbon, nitrogen, and oxygen nuclei in a chain process, called the
Carbon-Nitrogen-Oxygen chain, with several more steps. Regardless of the chain
process used, the net result of the fusion process is to fuse four hydrogen
nuclei (protons) to create one helium nucleus (2 protons + 2 neutrons) plus some
energy.
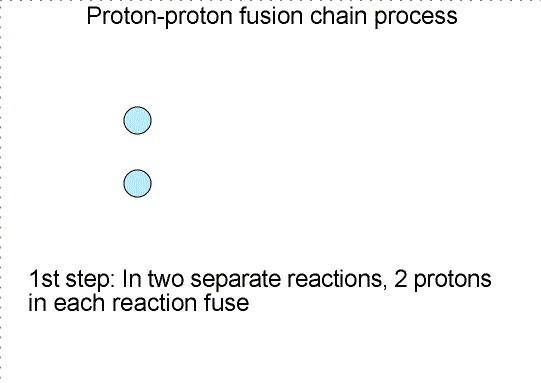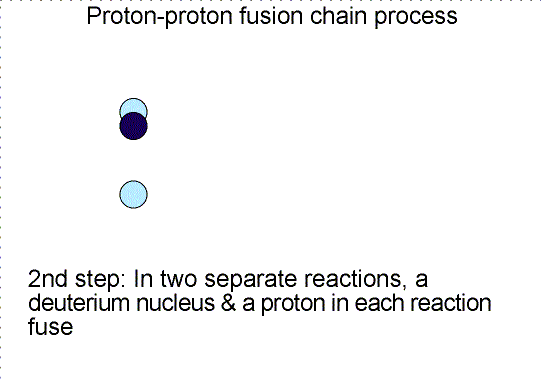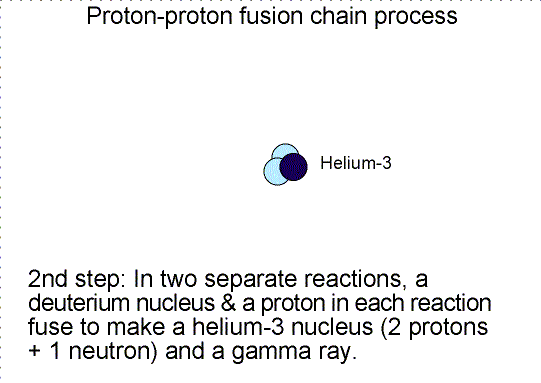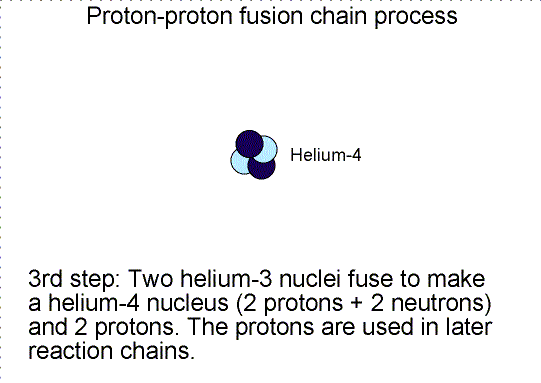
Three step nuclear
reaction chain. Selecting the image will bring up a single frame that summarizes
the chain reaction.
Why does nature use a long complicated chain reaction process to fuse four
protons into one helium nucleus? Would not it be much simpler if four protons
would collide simultaneously to make one helium nucleus? Simpler, but not very
likely is the answer. Getting four objects to collide simultaneously each with
high enough energy is very hard to do---the chances of this happening are very,
very small (as one from a family of 8 boys I can attest to the difficulty of
getting just half of us together for a mini-family reunion!). The chances of
this type of collision are too small to power the Sun, so nature has found a
cleverer scheme. The chances of two particles colliding and fusing is much
higher, so nature slowly builds up the helium nucleus.
Nuclear fusion is something of a holy grail for utility companies because it
produces no nasty waste products and has the potential of getting more energy
out of it than you put in---free energy! Unfortunately, the conditions to get
fusion to happen are very extreme by our standards. A major problem is
containing the very hot gas for extended periods of time to provide a sustained
energy source. We have been only able to tap the fusion process with the
Hydrogen bomb, but that is a one shot deal. The Hydrogen bomb still needs an
atomic bomb trigger to create the extreme temperatures needed for the fusion
process. At least you can get the waste product of the Sun's fusion process for
free with solar power collectors. The Sun can have a controlled fusion process
and not blow up all at once because of the hydrostatic equilibrium
``thermostat''.
Hydrostatic equilibrium is the balance between the thermal
pressures from the heat source pushing outwards and gravity trying to make the
star collapse to the very center. I will discuss hydrostatic
equilibrium in more depth (no pun intended) in a later section. The nuclear
fusion rate is very sensitive to temperature. It increases as roughly
temperature4 for the proton-proton chain and even more sharply
(temperature15) for the Carbon-Nitrogen-Oxygen chain. So a slight
increase in the temperature causes the fusion rate to increase by a large amount
and a slight decrease in the temperature causes a large decrease in the fusion
rate.
Now suppose the nuclear fusion rate speeds up for some reason. Then the
following sequence of events would happen: 1) the thermal pressure would
increase causing the star to expand; 2) the star would expand to a new point
where gravity would balance the thermal pressure; 3) but the expansion would
lower the temperature in the core---the nuclear fusion rate would slow down; 4)
the thermal pressure would then drop and the star would shrink; 5) the
temperature would rise again and the nuclear fusion rate would increase.
Stability would be re-established between the nuclear reation rates and the
gravity compression.
A similar type of scheme would occur if the nuclear fusion rate were to slow
down for some reason. The fusion rate stays approximately constant for stars
that are fusing hydrogen to make helium + energy in the core. Once the hydrogen
fuel in the core has been used up, hydrostatic equilibrium can no longer
stabilize the star. What happens next will have to wait until I talk about stellar
evolution.
- A.
- Need an energy source that lasts a long time: lifetime = energy
stored/luminosity. Nuclear fusion is the only process that can do this.
With nuclear fusion, lower-mass nuclei fuse together to form a single
more massive nucleus + energy. The sum of the low-mass nuclei masses = the
massive nucleus mass + energy/c2 (remember E = m
c2). The ``c'' is the symbol for the speed of light.
Nuclear fusion can power the Sun for about 10 billion years.
- B.
- To overcome the mutual electrical repulsion of positively-charged nuclei,
a star needs extremely high temperatures and densities. These conditions are
found only in the core of a star. Under these extreme conditions, particles
move fast enough to get close enough for strong nuclear force to overcome
electrical repulsion. Repulsive force increases with more positive charges.
Hydrogen is fused first because it requires less extreme conditions, than the
fusion of more massive nuclei.
- C.
- Stars use a chain process to fuse four hydrogen nuclei to create one
helium nucleus. A chain process is much more probable than a process that
fuses four hydrogen nuclei simultaneously. Most stars use a proton-proton
chain that is described in the animation above. Stars with enough mass
will also use the ``Carbon-Nitrogen-Oxygen chain'' process. The net process is
the fusion of four hydrogen nuclei to make one helium nucleus plus some
energy.
- D.
- The balance between gravity compression and outward thermal pressure
controls the rate of the nuclear fusion reactions. The star does not blow up
like a bomb.
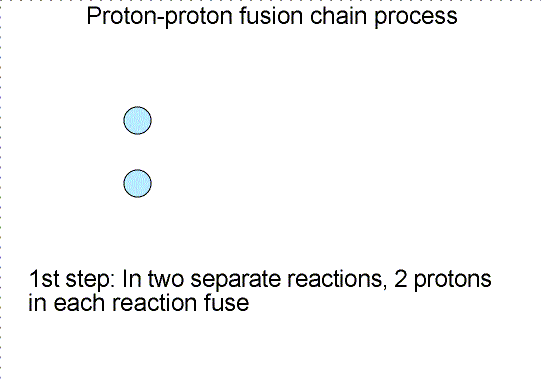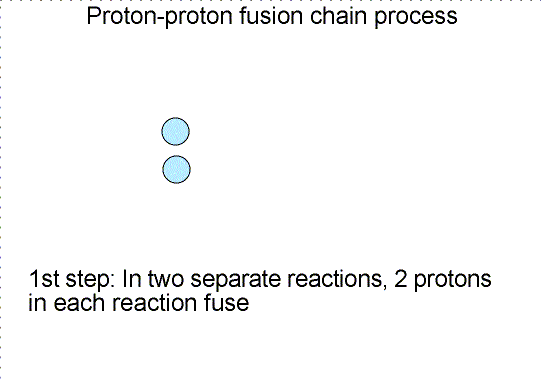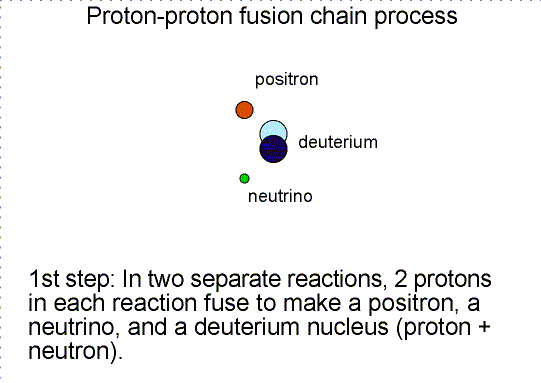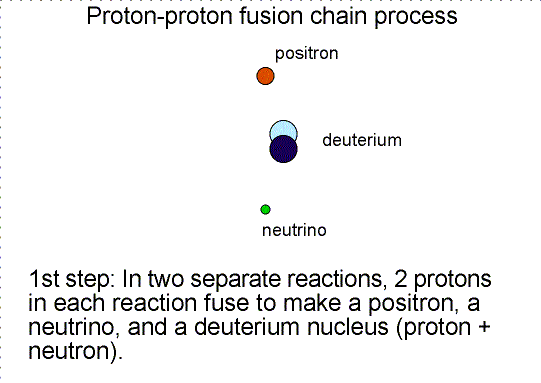
Helium is produced in the fusion of hydrogen. As
shown in the proton-proton fusion chain diagram above, there are two other
particles produced. One is the ``positron'' and the other is a ``neutrino''. A
positron is the antimatter counterpart of the electron. It has the same mass as
an electron but the opposite charge. When it collides with an electron, they
annihilate each other converting all of their mass into energy.
The photons produced in nuclear reactions take about a million years to move
from the core to the surface. The photons scatter off the dense gas particles in
the interior and move about a centimeter between collisions. In each collision
they transfer some of their energy to the gas particles. By the time photons
reach the photosphere, the gamma rays have become photons of much lower
energy---visible light photons. Because the photons now reaching the surface
were produced about a million years ago, they tell us about the conditions in
the core as it was a million years ago. The other particle produced in nuclear
reactions has a less tortuous path out of the core.
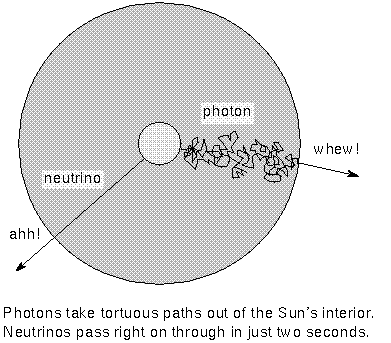
A neutrino is a massless (or very nearly massless) particle that
rarely interacts with ordinary matter. Neutrinos travel extremely fast---the
speed of light if they have zero mass or very close to the speed of light if
they have a small mass. Because they travel so fast and interact so rarely with
matter, neutrinos pass from the core of the Sun to the surface in only two
seconds. They take less than 8.5 minutes to travel the distance from the Sun to
the Earth. If you could detect them, the neutrinos would tell you about the
conditions in the Sun's core as it was only 8.5 minutes ago (much more current
information than the photons!).
The problem with neutrinos is that they have a very low probability of
interacting with matter. A neutrino could pass through a light year of lead and
not be stopped by any of the lead atoms! However, there are A LOT of neutrinos
produced by the Sun. Take a look at your pinky finger. In one second several
trillion neutrinos passed through your pinky (did you feel them?).
Don't worry, the neutrinos did not damage anything. The great majority of
neutrinos pass right through the materials around you.
Homestake Gold Mine
Neutrino Experiment (courtesy of R. Davis, Brookhaven National
Laboratory).
A few of them will interact with some matter on the Earth. You can increase
the odds of detecting a few of them by using a LARGE amount of a material that
reacts with neutrinos in a certain way. A chlorine isotope will change to a
radioactive isotope of argon when a neutrino interacts with it. In the same way
a gallium isotope will change to a radioactive isotope of germanium. Water
molecules will give off a flash of light when struck by a neutrino. Neutrino
detectors use hundreds of thousands of liters of of these materials in a
container buried under many tens of meters of rock to shield the detectors from
other energetic particles from space called cosmic rays. Even the
largest detectors detect only a few dozen neutrinos in a year.
Sudbury Neutrino
Observatory |
Super-Kamiokande Neutrino Detector water tank showing the
thousands of photon detectors each about the size of a beach
ball. |
As shown in the animation
describing the proton-proton chain above, the number of neutrinos produced in
the Sun is directly proportional to the number of nuclear reactions that are
taking place in the Sun's core. The same can also be said of the number of
neutrinos produced via the Carbon-Nitrogen-Oxygen chain. The more reactions
there are, the more neutrinos are produced and the more that should be detected
here on the Earth. The number of neutrinos detected coming from the Sun is
smaller than expected. Early experiments detected only 1/3 to 1/2 of
the expected number of neutrinos. These experiments used hundreds of thousands
of liters of cleaning fluid (composed of chlorine compounds) or very pure water.
They were sensitive to the high-energy neutrinos produced in less than one
percent of the nuclear fusion reactions. Later experiments using many tons of
gallium were able to detect the more abundant low-energy neutrinos. However,
those experiments also found the same problem---too few neutrinos (the gallium
experiments found about 2/3 the expected number). The puzzling lack of neutrinos
from the Sun is called the solar neutrino problem. There are several
possible reasons for this discrepancy between the observations and our
predictions:
- Nuclear fusion is not the Sun's power source. This reason is not supported
by other observations, so it is not likely to be the correct reason.
- The experiments were not calibrated correctly. It is unlikely that all of
the carefully-tuned experiments were tuned in the same wrong way. The
experiments have used three very different ways to detect neutrinos and have
produced the same lack of neutrinos. The experiments have been independently
verified by many other scientists, so astronomers think that the results are
correct, even if they are disappointing.
- The nuclear reaction rate in the Sun is lower than what our calculations
say. This is possible but many people have checked and re-checked the physics
of the reaction rates. There are some strong constraints in how much you can
lower the temperature in the core of the Sun to slow down the reactions.
Astronomers know how much total energy is emitted by the Sun, so they know
very accurately how many nuclear reactions are needed to produce all of those
photons seen coming from the Sun. Those reactions also produce the neutrinos.
Astronomers think they have a good idea of how stars produce their energy.
That leaves another alternative.
- Neutrinos produced in the core of the Sun change into other types of
neutrinos during their flight from the Sun to the Earth. Our neutrino
detectors can detect a certain kind of neutrino, called the ``electron
neutrino'', that are produced from nuclear fusion. Some of these electron
neutrinos may change into another of two types of neutrino that do not
interact with the detection material. This idea is gaining more and more
advocates. Some experiments suggest that the neutrinos may be able to change
into other types. New experiments are being constructed that will enable us to
detect all three types of neutrinos. Stay tuned!
A neutrino can change into another type of neutrino only if the neutrino
has some mass. If the neutrino has mass, then it cannot travel at the speed of
light, but can get darn close. Recent experiments have shown that the neutrino
does have a tiny amount of mass (several million times less than an electron).
A neutrino with even as small a mass as this has important consequences for
the evolution of the universe (more
about that later). It is amazing that in their effort to check their
nuclear fusion theory, astronomers have learned totally unexpected things
about fundamental physics and this has changed what is known about the
structure of the entire universe itself. Wow!
Here are some links
to the homepages of neutrino ``observatories'' that are in operation around the
world.
- The GALLEX
detector uses Gallium in 30 tons of Gallium trichloride to detect
neutrinos. It is buried far below a mountain in Italy. Their homepage also
provides links to good summaries of the other neutrino detectors.
- The Sudbury Neutrino
Observatory uses 1000 tons of ``heavy water'' buried far below ground
outside of Sudbury, Ontario (Canada) to detect the neutrinos. Heavy water uses
the deuterium isotope of hydrogen instead of the ordinary isotope of hydrogen
in the water molecule (H2O). Deuterium has 1 proton+1 neutron in
its nucleus instead of just the 1 proton of ordinary hydrogen. The extra
neutron makes deuterium twice as massive as ordinary hydrogen, so the ``heavy
water'' molecule is about 10% heavier than ordinary water. Included at the
site is a virtual
tour of the SNO detector.
- The Kamiokande
experiment in Japan uses 3000 metric tons of pure water to detect
neutrinos. This detector was the first one that could determine the direction
neutrinos were coming from. Also, it detected the neutrino burst from the
supernova explosion SN1987A that was discovered in a companion galaxy to our
Milky Way galaxy.
- A follow-up to the Kamiokande experiment is the Super-Kamiokande experiment
that is a joint-project of the United States and Japan. The detector will use
50,000 tons of water buried deep underground in Japan. The link takes you to
the United States
homepage at the University of Washington. The University of California at Irvine
is also involved in the project.
Two other sites worth exploring about neutrinos follow:
Go to
Sun section
Go to
Helioseismology and Star Structure section
last update: 06 April 1999
Is this page a copy of
Strobel's Astronomy Notes?
Author of original content:
Nick Strobel
