3C277.1 e-MERLIN workshop: Part 1 - Calibration

This guide offers a fundamental example for calibrating e-MERLIN C-Band (5 GHz) continuum data in CASA. It has been tested in CASA version 6.5 and is intended to operate using an averaged data set all_avg.ms (1.7 G), which requires at least 5.5 G of disk space to complete this tutorial. We expect that you have followed the CASA installation instructions on the EVN continuum tutorial homepage.

If you have a very slow laptop, you are advised to skip some of the plotms steps (see the plots linked to this page instead) and especially, do not use the plotms options to write out a png. This is not used in this web page, but if you run the script as provided, you are advised to comment out the calls to plotms or at least the part which writes a png, see tutors for guidance.

Table of Contents

  1. Guidance for calibrating 3C277.1 in CASA
    1. The data and supporting material
    2. How to use this guide
  2. Data inspection and flagging
    1. Check data: listobs and plotants (step 1)
    2. Identify 'late on source' bad data (step 2)
    3. Flag the bad data at the start of each scan (step 3)
    4. Flag the bad end channels (step 4)
    5. Identify and flag remaining bad data (step 5)
  3. Calibration
    1. Delay calibration (script step 6)
      1. Derive delay corrections.
    2. Setting the flux of the primary flux scale calibrator (script step 7)
    3. Derive the initial bandpass calibration and inspect effects (script step 8)
      1. Time-dependent pre-calibration to prepare for bandpass calibration
      2. Bandpass calibration
    4. Gain calibration (script step 9)
      1. Time-dependent phase calibration of all calibration sources
      2. Time-dependent amplitude calibration of all calibration sources
    5. Determining flux densities of calibration sources (script step 10)
      1. Derive calibrator flux densities
      2. Setting the calibrator flux densities
    6. Improved bandpass calibration (script step 11)
    7. Derive solutions for all cal sources with improved bandpass table (script step 12)
      1. Derive amplitude solutions
      2. Derive scan-averaged phase solutions to be applied to the target source
    8. Apply final calibrator source solutions and plot phase-ref and target (script step 13)
      1. Apply solutions
      2. Plot phase-ref and target amps against uv distance
    9. Split out target (script step 14)

1. Guidance for calibrating 3C277.1 in CASA

1A. The data and supporting material

For this part of the workshop, we only need four files in total. These can be obtained by extracting the files in 3C277_workshop_casa6.tar.gz, which can be found on the homepage for this workshop. Please double-check that you have the following in your current directory:

  • all_avg.ms - the data (after conversion to a measurement set).
  • 3C286_C.clean.model.tt0 - used for fluxscaling of the data set.
  • all_avg.flags.txt - pre-made flagging file to save time
  • 3C277.1_cal_outline.py - the script that we shall input values into to calibrate these data.
Note that some of these files may be tarred (i.e., they end in .tar.gz or .tar), so you will need to use tar -xzvf <filename> to extract them.

1B. How to use this guide

This user guide presents inputs for CASA tasks, e.g., gaincal, to be entered interactively at a terminal prompt for calibrating the averaged data and initial target imaging. This is useful for examining your options and checking for syntax errors. You can run the task directly by typing gaincal at the prompt. If you want to change parameters and run it again, ensure that you delete the calibration table (make sure you get the right one) before re-running. You can review these by typing: 

# In CASA
!more gaincal.last

This will output something like: 

taskname           = "gaincal"
vis                =  "all_avg.ms"
caltable           =  "bpcals_precal.ap1"
...
...

#gaincal(vis="all_avg.ms",caltable="bpcals_precal.ap1",field="1407+284",spw="",intent="",
selectdata=True,timerange="",uvrange="",antenna="",scan="",observation="",msselect="",solint="120s",
combine="",preavg=-1.0,refant="Mk2",minblperant=2,minsnr=2,solnorm=True,gaintype="G",smodel=[],
calmode="ap",append=True,splinetime=3600.0,npointaver=3,phasewrap=180.0,docallib=False,callib="",
gaintable=['all_avg.K', 'bpcals_precal.p1'],gainfield=[''],interp=[],spwmap=[],parang=False)

As you can see in the script, the second format (without '#') is the version to use in the script, with a comma following each parameter value. Once you are satisfied with the values you have set for each parameter, enter them in the script 3C277.1_cal_outline.py (or whatever you have named it). You can omit parameters for which you have not set values; the defaults will apply for these (see e.g., help(gaincal) for what they are), but feel free to experiment if time permits.

The script already includes most of the plotting inputs to save time. Create and examine the plots; modify the inputs as desired, zoom in, etc. There are links to copies of the plots (or parts of the plots), but only click on them after attempting on your own or if you encounter difficulties.

The parameters that should be set explicitly or require explanation are provided below, marked with "**" if they need values inserted.

If you have already plotted the antenna positions with plotants, you will have noticed that Mk2 has many short baselines, which makes it more likely to provide good calibration solutions and serves as a reliable reference antenna (refant).

The input measurement set all_avg.ms contains five fields:

eMERLIN name Common name Role
1252+5634 3C277.1 target
1302+5748 J1302+5748 phase reference source
1407+284 OQ208 bandpass cal. (usually about 2 Jy at 5-6 GHz)
0319+415 3C84 bandpass, polarisation leakage cal. (usually 10-20 Jy at 5-6 GHz)
1331+305 3C286 flux, polarisation angle cal. (flux density known accurately, see Step 7)
These data were collected in full polarisation with a bandwidth of 0.512 GHz centred at 5072 MHz, across four adjacent spectral windows (spws, also known as IFs). Each 128-MHz spw contains 512 channels, each 0.25 MHz wide, and 1-second integrations were used (the data are later averaged).

These data have already been preprocessed from the original raw FITS IDI files, which included the following:

  1. Conversion from FITS IDI to a CASA-compatible measurement set.
  2. Sorted and recalculated the $uvw$ (visibility coordinates), combined all data, and adjusted scan numbers to increment with each source change.
  3. Averaged every 8 channels and 4 seconds.

2. Data Inspection and Flagging

2A. Check data: listobs and plotants (script step 1)

← back to top

Ensure you have all_avg.ms in a directory that has enough space, and then start CASA.

Enter the parameter in step 1 of the script to specify the measurement set and, optionally, the parameter to save the listing to a text file. Important: To facilitate understanding, the line numbers corresponding to the script 3C277.1_cal_outline.py are included in the excerpts from the script presented in this tutorial. 

	listobs(vis='**',
			overwrite=True,
			listfile='**')

Due to e-MERLIN storing data for each source in a separate fitsidi file, the sources are listed individually even though the phase-ref and target scans interleave. Consequently, selected entries from listobs, reordered by time, display: 

Timerange (UTC)          Scan  FldId FieldName             nRows
  SpwIds   Average Interval(s)  #(i.e. RR RL LR LL integration time) 05-May-2015
...
20:02:08.0 - 20:05:08.5     7      0 1302+5748                 2760  [0,1,2,3]  [3.91, 3.91, 3.91, 3.91]    # phase-ref
20:05:11.0 - 20:12:33.5    72      1 1252+5634                 6660  [0,1,2,3]  [3.98, 3.98, 3.98, 3.98]    # target
20:12:36.0 - 20:15:34.5     8      0 1302+5748                 2700  [0,1,2,3]  [3.96, 3.96, 3.96, 3.96]    # phase-ref
...
22:02:04.0 - 22:47:00.5   132      2 1331+305                 40500  [0, 1, 2, 3]  [3.99, 3.99, 3.99, 3.99] # flux scale/pol angle calibrator
22:47:03.0 - 23:29:59.5   133      3 1407+284                 38700  [0, 1, 2, 3]  [3.99, 3.99, 3.99, 3.99] # bandpass calibrator
06-May-2015
07:30:03.0 - 08:29:59.5   134      4 0319+415                 54000  [0, 1, 2, 3]  [4, 4, 4, 4]             # bandpass/leakage calibrator

There are four spectral windows: 

 SpwID  Name   #Chans   Frame   Ch0(MHz)  ChanWid(kHz)  TotBW(kHz) CtrFreq(MHz)  Corrs
  0      none      64   TOPO    4817.000      2000.000    128000.0   4880.0000   RR  RL  LR  LL
  1      none      64   TOPO    4945.000      2000.000    128000.0   5008.0000   RR  RL  LR  LL
  2      none      64   TOPO    5073.000      2000.000    128000.0   5136.0000   RR  RL  LR  LL
  3      none      64   TOPO    5201.000      2000.000    128000.0   5264.0000   RR  RL  LR  LL

And six antennae: 

ID   Name  Station       Diam.    Long.         Lat.                 ITRF Geocentric coordinates (m)
  0    Mk2   e-MERLIN:02 24.0 m   -002.18.08.9  +53.02.58.7     3822473.365000  -153692.318000  5085851.303000
  1    Kn    e-MERLIN:05 25.0 m   -002.59.44.9  +52.36.18.4     3859711.503000  -201995.077000  5056134.251000
  2    De    e-MERLIN:06 25.0 m   -002.08.35.0  +51.54.50.9     3923069.171000  -146804.368000  5009320.528000
  3    Pi    e-MERLIN:07 25.0 m   -002.26.38.3  +53.06.16.2     3817176.561000  -162921.179000  5089462.057000
  4    Da    e-MERLIN:08 25.0 m   -002.32.03.3  +52.58.18.5     3828714.513000  -169458.995000  5080647.749000
  5    Cm    e-MERLIN:09 32.0 m   +000.02.19.5  +51.58.50.2     3919982.752000     2651.982000  5013849.826000

Provide one parameter to plot the antenna positions (optionally, a second parameter to save this as a PNG). 

	plotants(vis='**', figfile='**')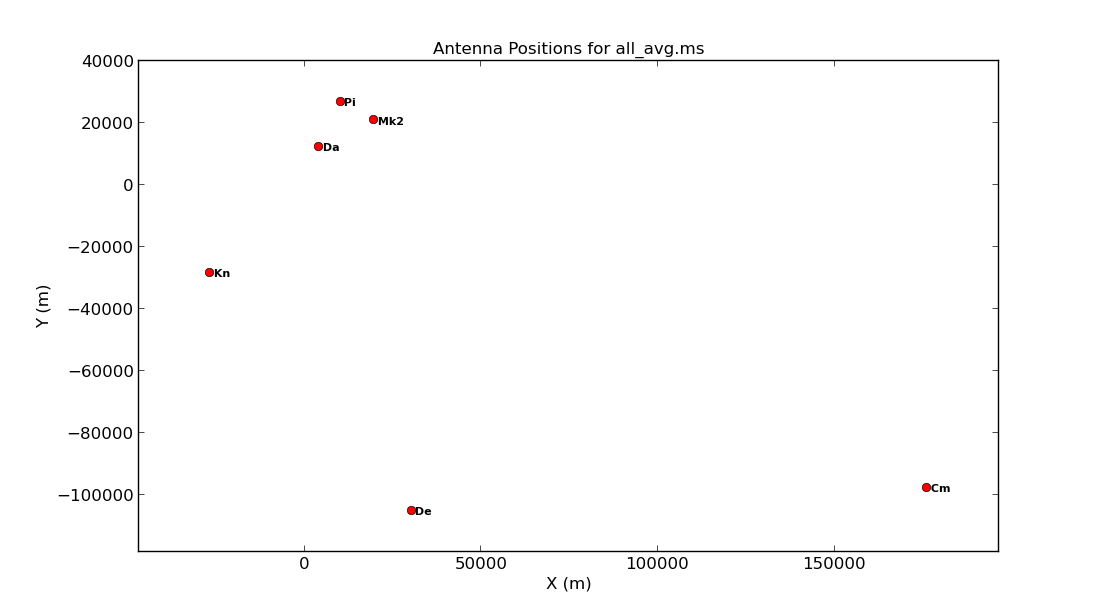

Consider what would constitute a good reference antenna. While Cambridge has the largest diameter, it lacks short baselines.

Plot the $uv$ coverage of the data for the phase-referenced source. Refer to the annotated listobs output above to identify it. You need to enter several parameters, but some have already been completed for you: 

	plotms(vis='**',
		   xaxis='**',
		   yaxis='**',
		   coloraxis='spw',
		   avgchannel='8',
		   field='1302+5748',
		   showgui=gui)

Please note that we averaged the channels slightly to prevent overloading your computer. If this process takes too long, feel free to proceed to the plot below. The $u$ and $v$ coordinates represent (wavelength/projected baseline) as the Earth rotates while the source is being observed. Consequently, since each spw is at a different wavelength, it samples a distinct portion of the uv plane, enhancing aperture coverage of the source and enabling Multi-Frequency Synthesis (MFS) of continuum sources.

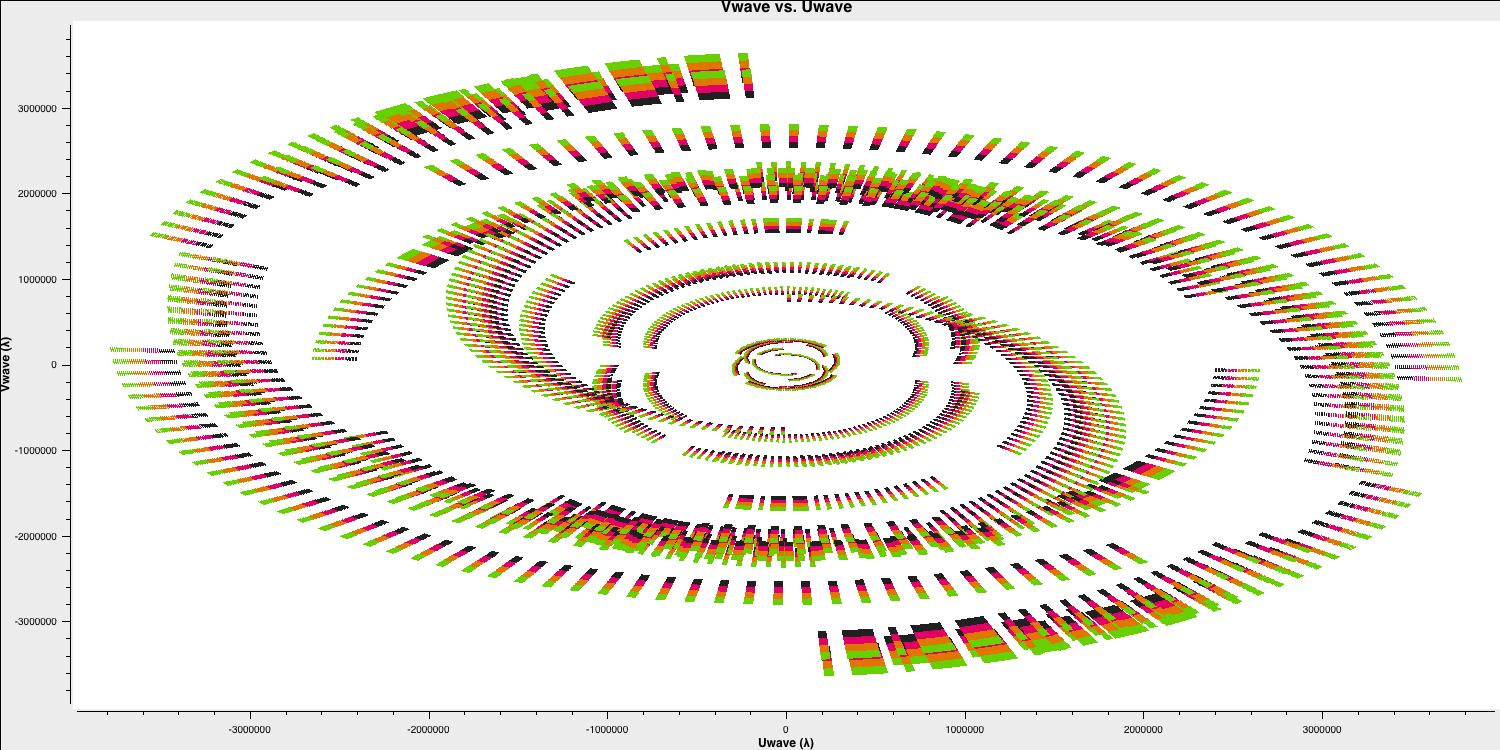
If you are satisfied with your entries, proceed with step 1, and you should see these two plots in your current directory. Remember, we execute a step using the following syntax in the CASA prompt: 

runsteps=[1]
execfile('3C277.1_cal_outline.py')

2B. Identify 'late on source' bad data (step 2)

← back to top

Use plotms to plot the amplitudes of the phase-reference source as a function of time. A few central channels are selected and averaged, providing a good signal-to-noise ratio while preventing excessive phase errors across the band from causing decorrelation (in practice, you may need to experiment with various selections or plot phase versus channel to determine the best choice). Some guidance on proper parameter selection is provided in the code blocks below. 

	plotms(vis='***',
		   field='***',  # phase ref
		   spw='***',    # plot just the inner 3/8 of the channels for each spw (see listobs output)
		   avgchannel=***, # average these channels
		   xaxis='***', yaxis='***',
		   antenna=antref+'&**', # This uses Mk2 as refant for ease of comparison but another with many short baselines could be used.
		   correlation='**,**',  # Just select the parallel hands, since the cross hands (polarised intensity) are much fainter.
		   coloraxis='corr', # Color by baseline or correlation as you prefer
		   showgui=True,
		   overwrite=True, plotfile='')

Once you have entered the parameters, proceed to step 2. Be aware that you can modify the parameters interactively after plotms has started.

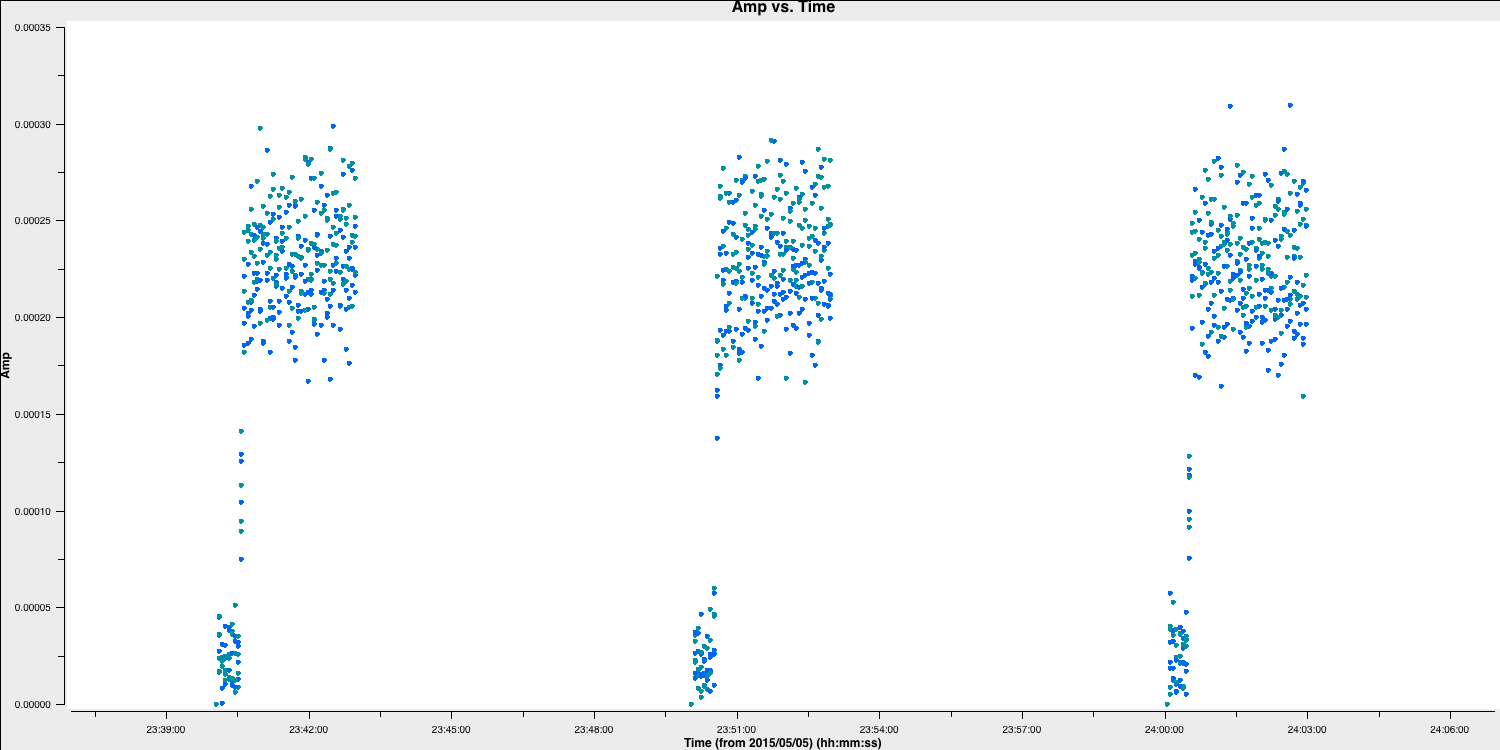
Roughly the same interval at the start of each scan is bad for all sources and antennas, making the phase reference a valuable source to examine. (In a few cases, there is additional bad data; ignore that for now.) Use the zoom feature and display to estimate the time interval (as shown in the above plot), and we will enter that value in the next part.

2C. Flag the bad data at the start of each scan (step 3)

← back to top

Remember from the EVN continuum tutorial that we must always back up our flags before we do any further flagging. This way, we won't have to return to the beginning if we accidentally flag or unflag large amounts of good data. We use flagmanager for this. 

	# Back up original flag state
	flagmanager(vis='***',
				mode='***',
				versionname='pre_quack')

If the parameters are set correctly, we should have a backup named pre_quack in the all_avg.ms.flagversions file. You can verify its existence by running flagmanager again with mode='list' instead.

Next, we need to perform the quacking or flagging of these channels. We use the CASA task flagdata for this, along with a special mode called quack. Fill in the flagdata parameters by inserting the time that the antennas were off source, which we determined earlier. 

	# Flag first 40 s of each scan for all sources
	flagdata(vis='***',
			 mode='***', quackinterval='**')

Re-plot in plotms (select the reload option and replot if you still have it open) to verify that the bad data at the beginning of each scan is eliminated. There are still some irregular periods of bad data, which will be flagged later.

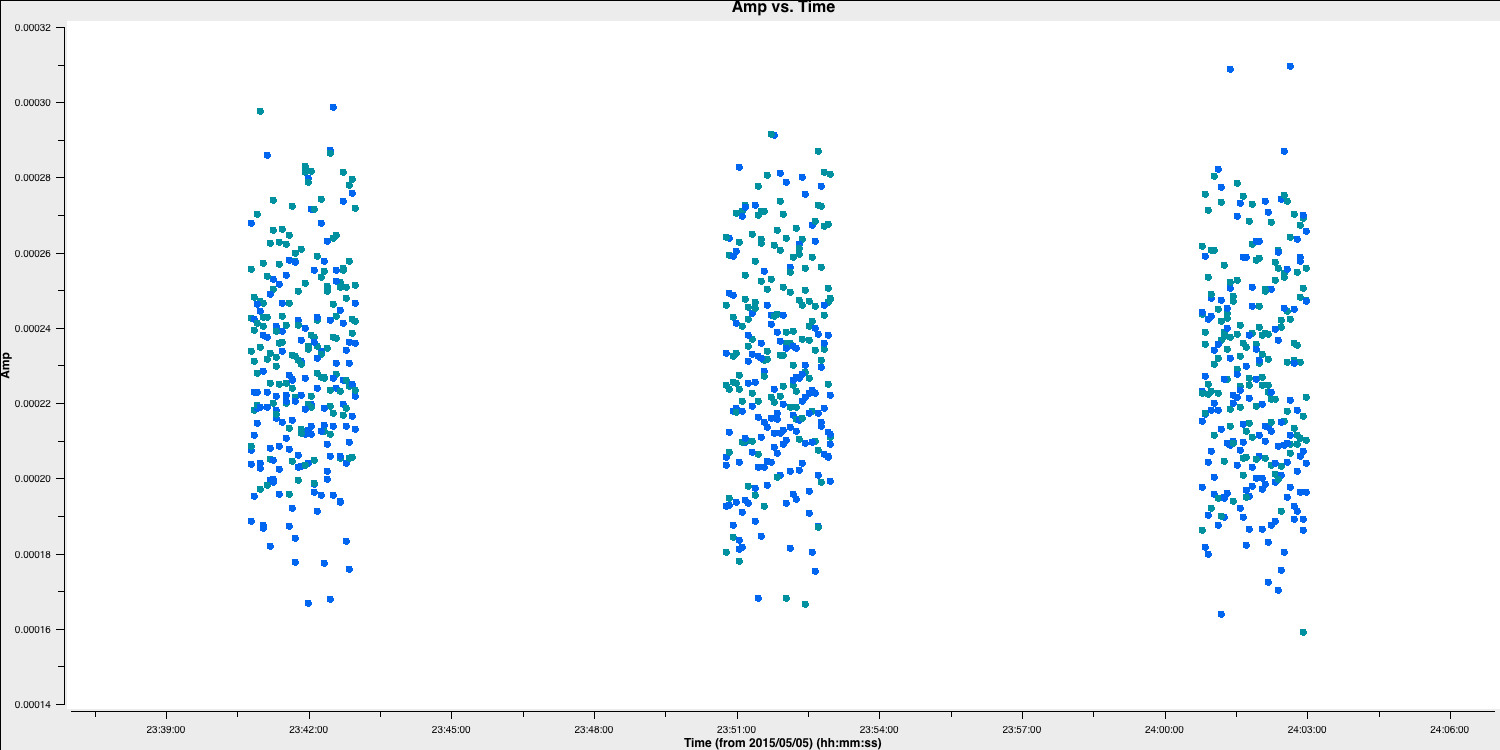
2D. Flag the bad end channels (step 4)

← back to top

In this step, we will perform both plotting and flagging simultaneously. To obtain the correct parameters for the flagging, it is advisable to copy and paste the plotms commands (with the appropriate parameters) into your CASA prompt and then enter these parameters into the 3C277.1_cal_outline.py code for future reference.

Let's continue. The edges of the bandpass for each spw exhibit low sensitivity and must be flagged. This applies to all sources, polarisations, and antennas, although different spectral windows may vary. Just observe the brightest source, 0319+415. 

	plotms(vis='***',
		   field='***',
		   xaxis='***', yaxis='***', # plot amplitude against channel
		   antenna=***,             # select one baseline
		   correlation='**,**',     # just parallel hands
		   avgtime='***',           # set to a large number
		   avgscan=****,            # average all scans
		   iteraxis='***', coloraxis='***',  # view each spectral window in turn, and color
		   showgui=True,                     # change to False if you want ,
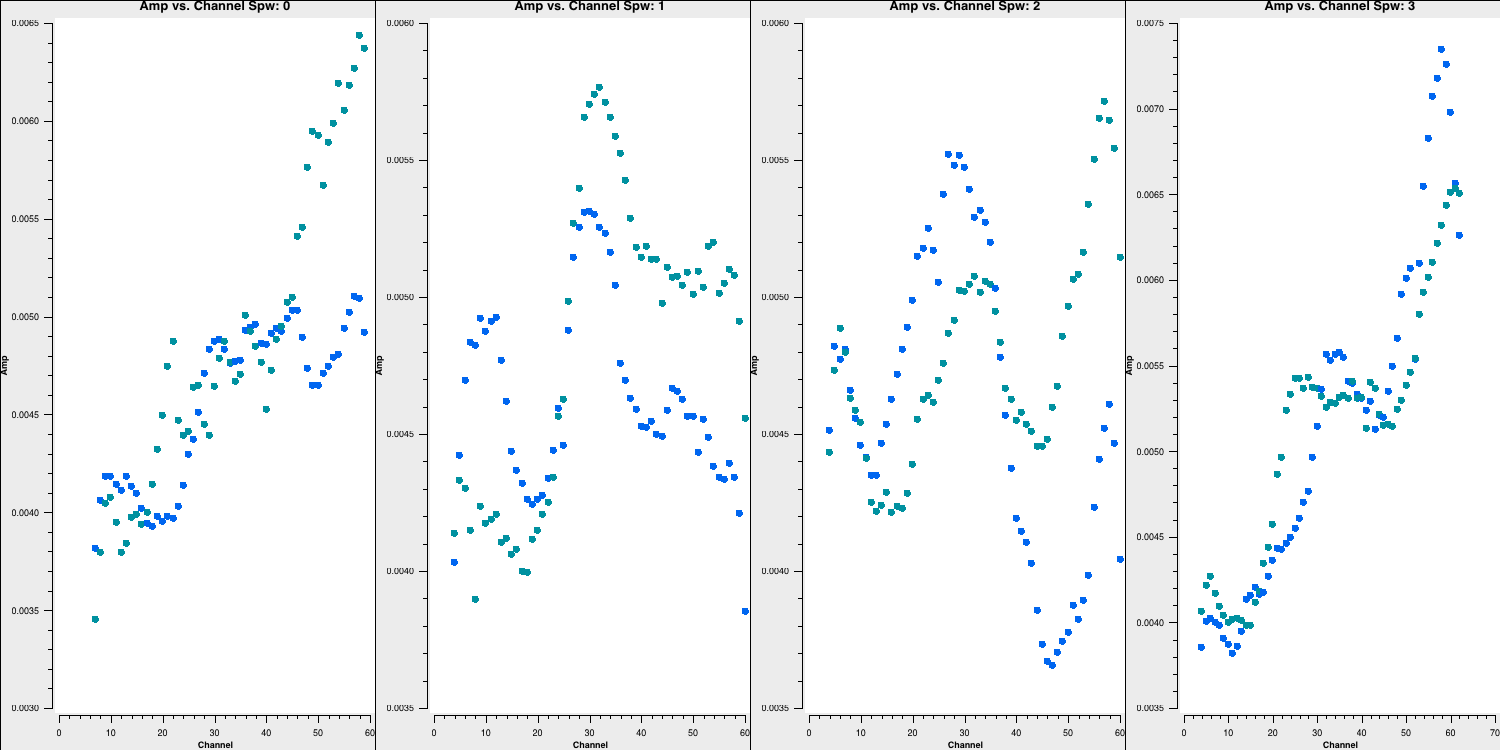
		   overwrite=True, plotfile='')

Observe the channel ranges that are considerably less sensitive at both ends of each spectral window.

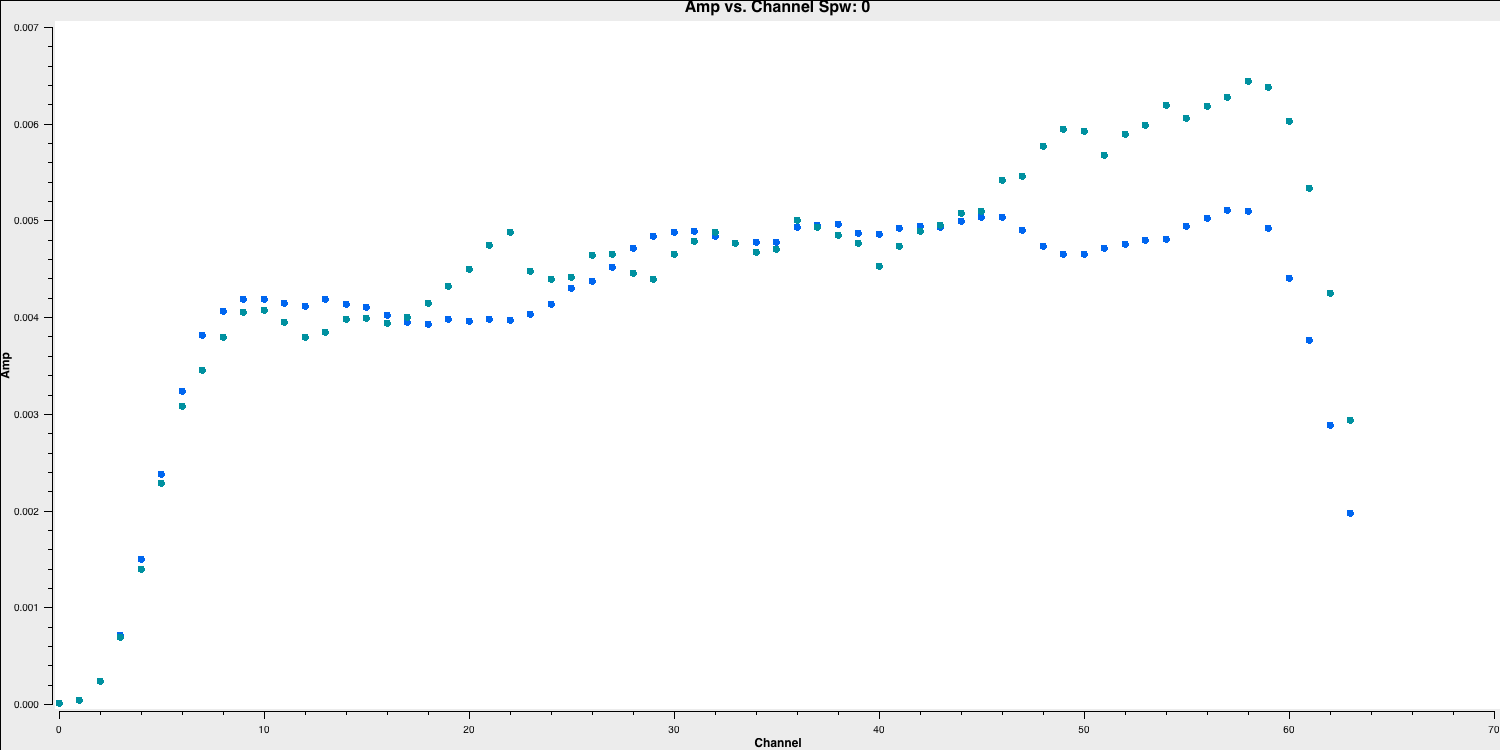
Back up the flags and enter the appropriate parameters in flagdata. Note the unusual CASA notation for selecting spectral windows and channels. We have provided the "bad"/insensitive channels in spw 0 with the correct syntax, so use that as a reference for the other spectral windows. 

	# Back up flags
	flagmanager(vis='***',
				mode='***',
				versionname='pre_endchans')

	# end chans
	flagdata(vis='***',mode='***',
			 spw='0:0~6;60~63,***')  # enter the ranges to be flagged for the other spw

Carry out step 4, then re-plot using plotms (the code should already manage this replotting for you!)

2E. Identify and flag remaining bad data (step 5)

← back to top

Finally, you usually have to go through all baselines, average channels, and plot amplitude against time. To save time (and your sanity!), you don't have to do everything here. Take a look at 0319+419 and write down a few commands. This is done in the form of a list file, which contains no commas, and the only spaces must be a single space between each parameter for a given flagging command line. Some errors affect all baselines connected to a given antenna, while others (e.g. correlator problems) may affect only one baseline. Typically, all spw will be affected, so you can inspect just one, but check afterwards that all are 'clean'. It can be hard to determine what is good or bad for a faint target, but if the phase reference is poor for longer than a single scan, then usually the target will be poor for the intervening time. Since the data is collected over two days, it is safest to use the full date for any time range.

Before we start flagging, remember to back up the flags again! 

	flagmanager(vis='**',
				mode='**',
				versionname='pre_timeflagging')

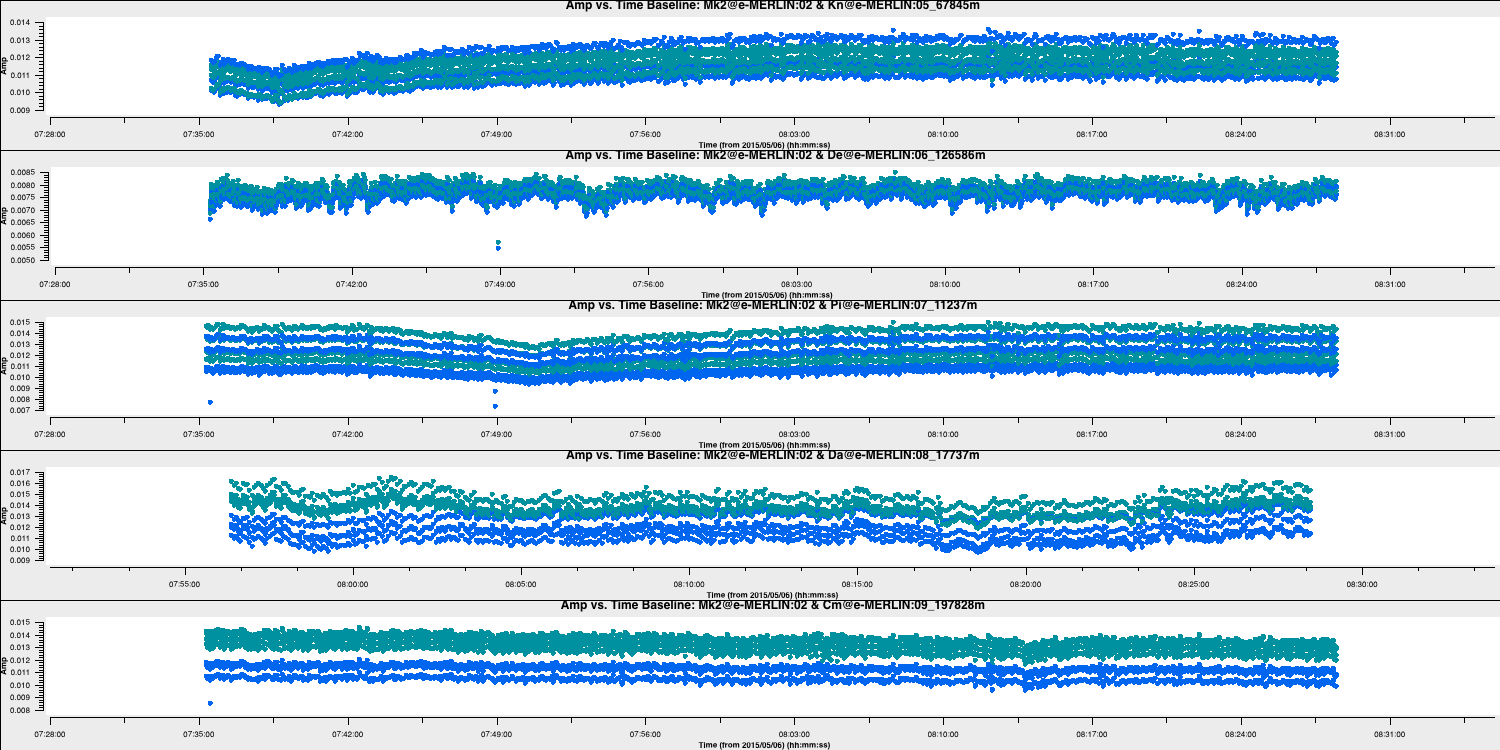
Use plotms to inspect 0319+415 by plotting amplitude against time for RR and LL only, averaging all channels and baselines to Mk2, while paging (iterating) through the baselines.

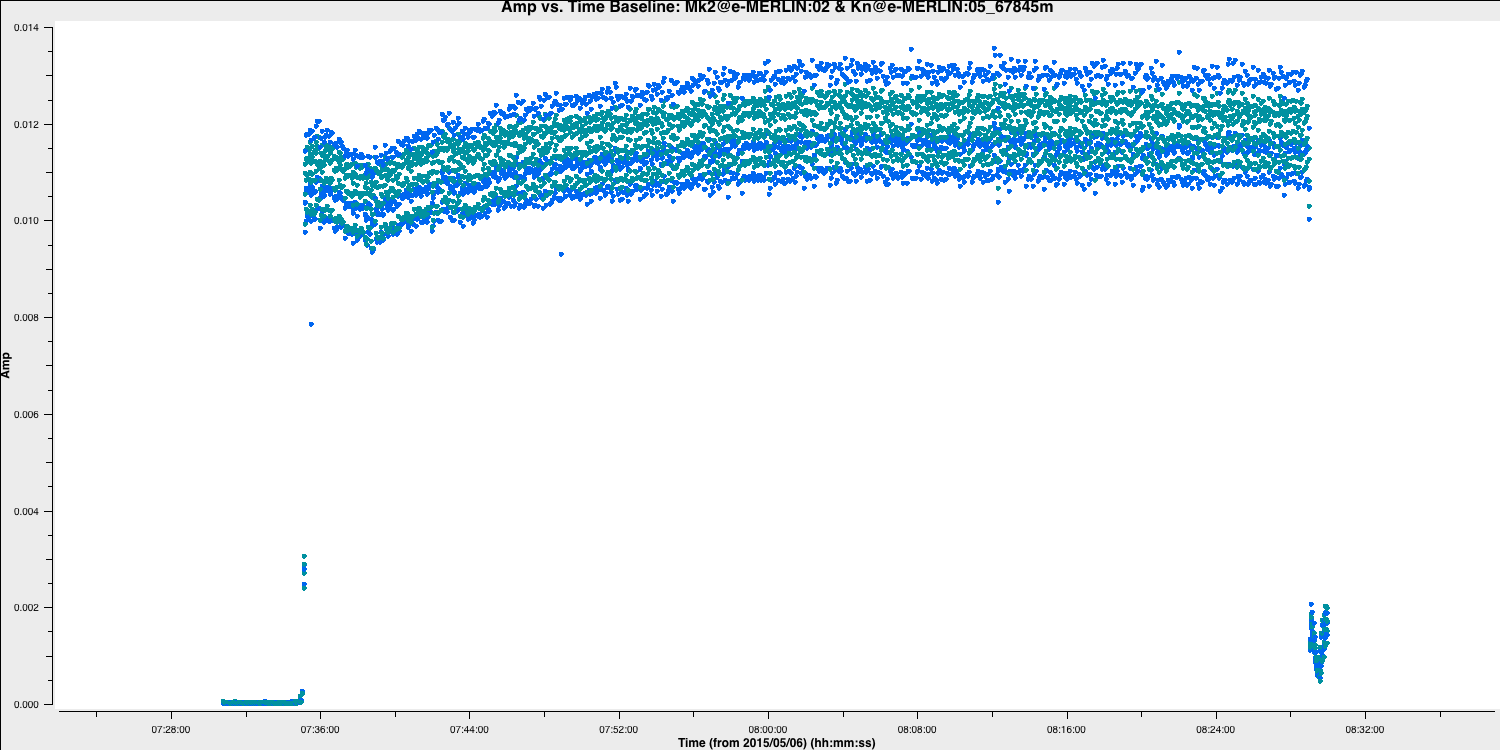
Here is a list of some of the flagging commands for the data shown below: 

mode='manual' field='0319+415' timerange='2015/05/06/07:30:00~07:35:00'
mode='manual' field='0319+415' antenna='Da' timerange='2015/05/06/07:30:00~07:56:22'
mode='manual' field='0319+415' antenna='Mk2&Kn' timerange='2015/05/06/07:30:00~07:35:34'
mode='manual' field='0319+415' antenna='Mk2&Kn' timerange='2015/05/06/07:48:55~07:48:58'
mode='manual' field='0319+415' antenna='Mk2,De' timerange='2015/05/06/07:35:00~07:35:18'
mode='manual' field='0319+415' timerange='2015/05/06/08:28:30~08:30:00'

Note that by paging through all the baselines, you can determine which bad data affects which antennas. Take a look at 1331+305 and write its commands.

The commands are applied in flagdata using mode='list' and inpfile='***', where inpfile refers to the name of the flagging file.

Create a file named all_avg_user.flags.txt that contains all the commands to flag bad data. Then, apply it in flagdata using mode='list'. Carefully monitor the messages in the logger and terminal for any reported syntax errors.

Alternatively, if you’re short on time and wish to avoid flagging, instead add all_avg.flags.txt as the inpfile command; it will flag all the data when you execute step 5.

Step 5 will also re-plot the data, so ensure that it is now clean.

3. Calibration

3A. Delay calibration

← back to top

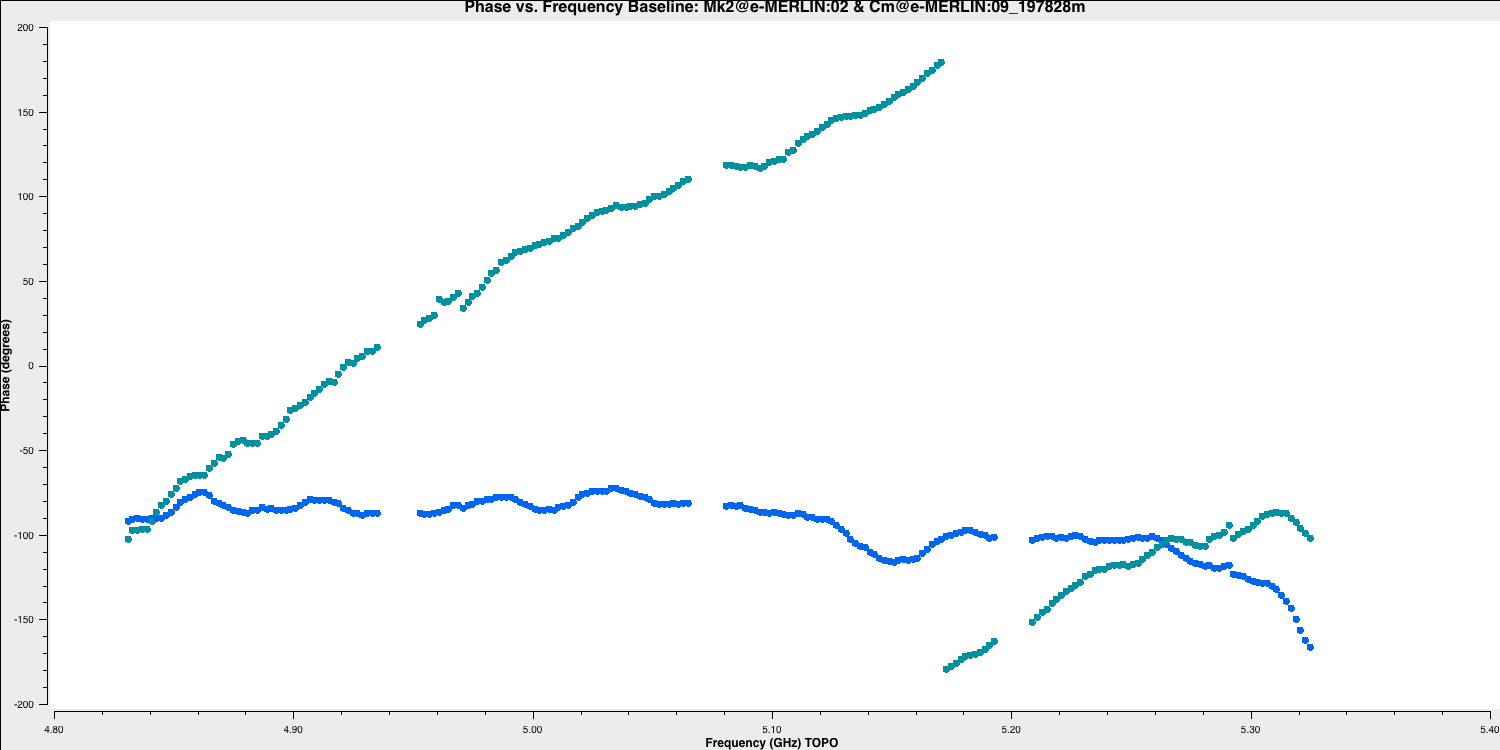
In this next part, we will look at calibrating this data. We will start by making the delay corrections (the slope of frequency versus phase). First, plot the raw phase against frequency for a bright source, which is typically a bandpass calibrator. Its advisable to copy these plotting commands into your CASA prompt instead of using the script. 

	plotms(vis='all_avg.ms', field='0319+415', xaxis='frequency',
		   gridrows=1,gridcols=1,iteraxis='baseline', # Plot multiple baselines on one page
		   yaxis='phase',ydatacolumn='data',antenna=antref+'&*', # Plot all baselines to the reference antenna
		   avgtime='600',avgscan=True,correlation='LL,RR', # Average 10 min
		   coloraxis='corr',
		   plotfile='',
		   overwrite=True)

The y-axis spans from -200 to +200 degrees, and some data shows a slope of about a full 360 degrees across the 512-MHz bandwidth. Considering the baseline in Cambridge, reflect on the following questions.

QUESTION 1: What is the apparent delay error this corresponds to? What will be the effect on the amplitudes? Answer A change of $2\pi$ radians in $x$ Hz results from a delay error of $1/x$ sec. Thus, a change of 360 degrees in 512 MHz is caused by a delay error of $1/(512\times 10^{6})\,\mathrm{sec} \sim 2\,\mathrm{ns}$. If data are vector-averaged across a phase slope, the amplitudes will be reduced, with a larger reduction corresponding to greater phase change in the averaging interval. Therefore, if the combined phase change on a baseline is more pronounced in one polarisation than the other, that polarisation will exhibit a lower averaged apparent amplitude.

QUESTION 2: Delay corrections are calculated relative to a reference antenna, which has its phase assumed to be zero. Therefore, the corrections factored for other antennas include any correction due to the reference antenna. Roughly, what do you expect the magnitude of the Cm corrections to be? Do you expect the two hands of polarisation to have the same sign? Answer The slopes on Mk2 correspond to approximately 1 turn per 512 MHz, in the same sense for both LL and RR. The slopes on Cm correspond to less than half a turn in the same sense for one polarisation and about a full turn in the opposite sense for the other. Therefore, the combination of errors, which will be completely resolved by correcting Cm, corresponds to magnitudes of $\lesssim 1\,\mathrm{ns}$ and $ \sim 4\,\mathrm{ns}$ for the two polarisations, with opposite signs. The slopes, and hence the actual values, vary between spw, as seen in the delay correction plot.

Plot amplitude against time for just one channel per spw: 

	# amp against time, longest baseline, single channel
	plotms(vis='all_avg.ms', field='0319+415',
		   spw='0~3:55', ydatacolumn='data',                     # Just one channel per spw
		   yaxis='amp', xaxis='time', plotrange=[-1,-1,0,0.018], # Plot amplitude v. time with fixed y scale
		   avgtime='60',correlation='RR', antenna=antref+'&Cm',  # 60-sec average, one baseline/pol
		   coloraxis='spw',plotfile='',
		   showgui=True,
		   overwrite=True)

Repeat with all channels averaged: 

	# amp against time, longest baseline, average all channels
	plotms(vis='all_avg.ms', field='0319+415',
		   xaxis='time', yaxis='amp',ydatacolumn='data',         # Plot amplitude v. time with fixed y scale
		   spw='0~3',avgchannel='64',                            # Average all unflagged channels
		   antenna=antref+'&Cm', avgtime='60',correlation='RR',  # 60-sec average, one baseline/pol
		   plotfile='',
		   plotrange=[-1,-1,0,0.018],coloraxis='spw',
		   showgui=True,
		   overwrite=True)

For consistent y-axis scaling, these plots have been created in Python. However, your plotms outputs should be somewhat identical.

QUESTION 3: In the plots, which has the higher amplitudes: the channel-averaged data or the single channel? Why? Answer The single channel exhibits higher amplitudes. The source 3C84 is very bright, resulting in plenty of signal in each individual channel. However, averaging over all channels when there is a large phase slope leads to a decorrelation of amplitudes, causing the channel-averaged data to show reduced amplitudes. A similar effect occurs if the data contains phase errors as a function of time and is averaged over too long a period.

3A i. Derive delay corrections

← back to top

The CASA task gaincal is used to derive most calibrations. Type inp gaincal or help gaincal to find out more. Complete the '**' fields. 

	# Derive gain solutions
	os.system('rm -rf all_avg.K') # Remove any old version
	gaincal(vis='all_avg.ms',
			gaintype='**',            # Delay calibration (see help gaincal)
			field=calsources,         # All calibration sources
			caltable='all_avg.K',     # Output table containing corrections
			spw='0~3',solint='**',    # 600s solution interval
			refant='**',              # Reference antenna (phase set to 0)
			minblperant=2,            # For each antenna and solint, require solutions on
			minsnr=2)                 # at least 2 baselines with S/N > 2

Examine the solutions. Do they match the expected magnitude? 

	plotms(vis='all_avg.K',
		   gridrows=2,
		   gridcols=3,
		   xaxis='**',
		   yaxis='**', # Plot delay against time
		   iteraxis='antenna', # Each antenna in a separate pane, coloured by spw
		   coloraxis='spw',
		   plotfile='all_avg.K.png')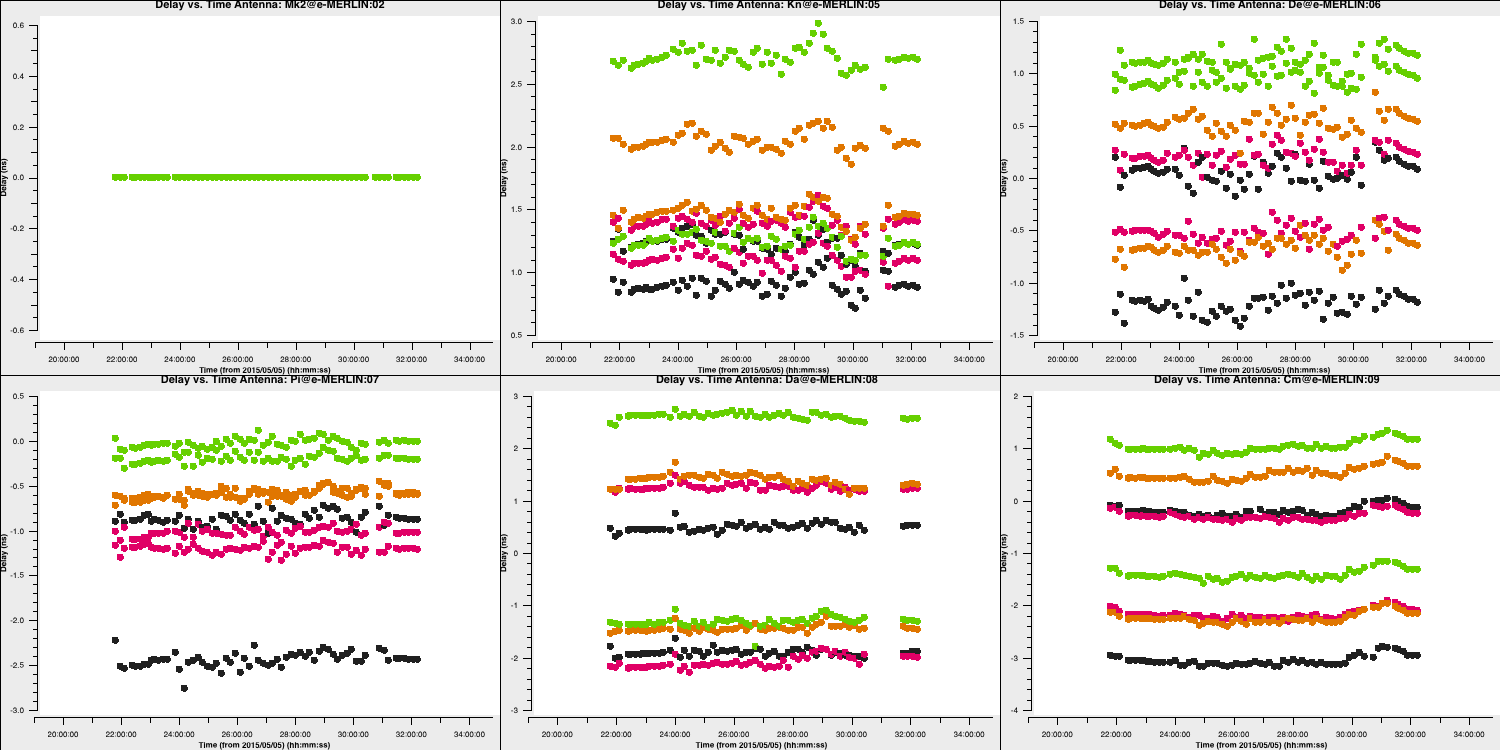

These solutions remain stable over time, indicating that the solutions can be applied to the target.

3B. Setting the flux of the primary flux scale calibrator (script step 7)

← back to top

1331+305 (3C286) is an almost non-variable radio galaxy, and its total flux density is well established as a function of time and frequency (Perley & Butler 2013) . It is somewhat resolved by e-MERLIN, so we use a model created from a $\sim$12-hour observation centred on 5.5 GHz. This model is scaled to the current observing frequency range (approximately 5 GHz) using setjy, which computes the appropriate total flux density, spectral index, and curvature based on parameters from Perley & Butler (2013).

However, a small percentage of the flux is resolved out by e-MERLIN; the simplest current method to account for this is to later scale the fluxes derived from the other calibration sources by 0.938, based on calculations for e-MERLIN by Fenech et al.

The model consists of a set of CLEAN components (see the imaging steps in the EVN continuum tutorial for more information), and setjy includes these in the measurement set so that their Fourier transform can be used as a model to later compare with the actual visibility amplitudes. If you make an error (e.g., set a model for the incorrect source), use the task delmod to remove it. 

	setjy(vis='**',
		  field='**',
		  standard='Perley-Butler 2013',
		  model='**')  # You should have downloaded and untar'd this model

By default, setjy scales the model for each channel, as observed when plotting the model amplitudes against $uv$ distance, coloured by spectral window. If you have plotms running, access the axes and select the model, or refer to the script for inputs. The model only appears for the baselines present during the short time interval when 1331+305 was observed here. If not, copy the following code for plotms. 

	os.system('rm -rf 3C286_model.png')
	plotms(vis='all_avg.ms', field='1331+305', xaxis='uvwave',
		   yaxis='amp', coloraxis='spw',ydatacolumn='model',
		   correlation='LL,RR',
		   showgui=True,
		   symbolsize=4, plotfile='')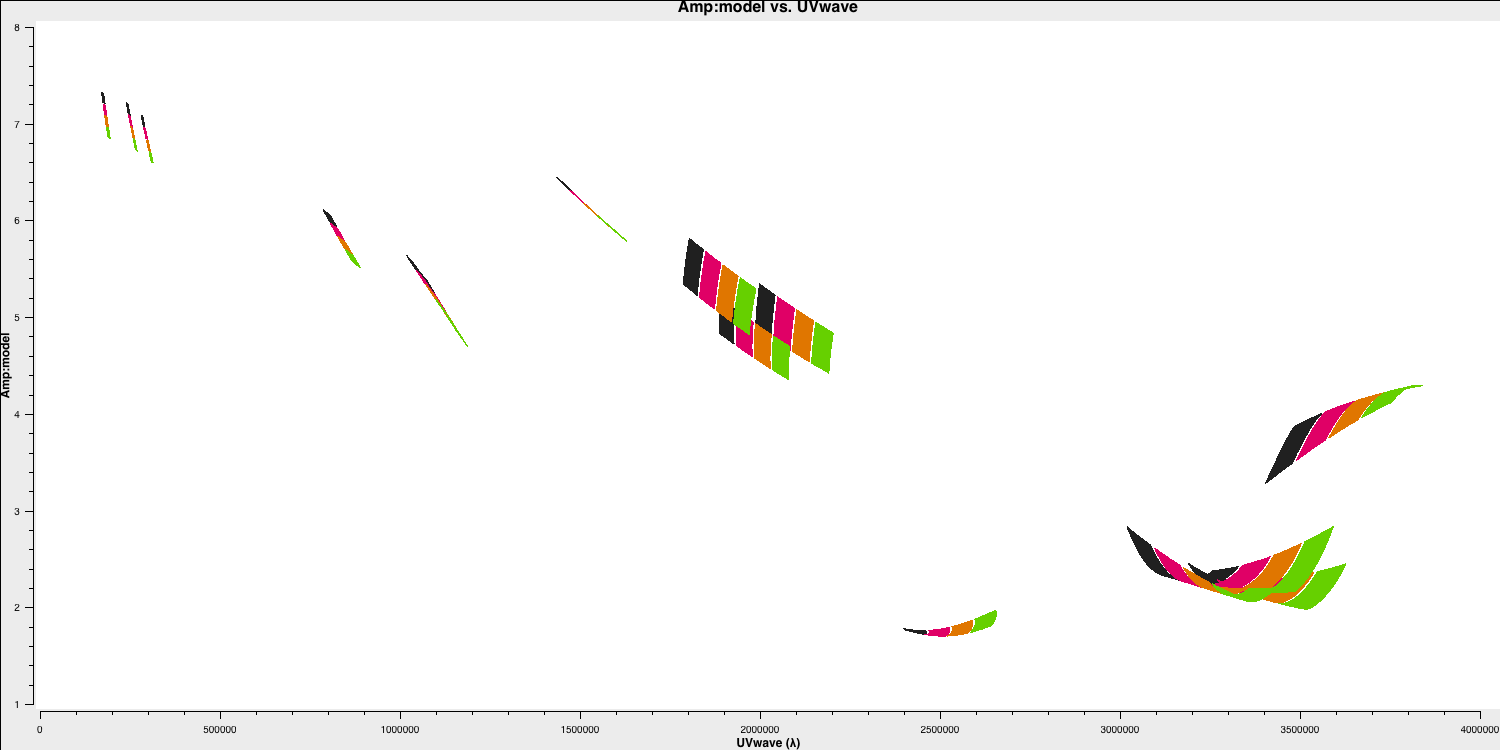

3C. Derive the initial bandpass calibration and inspect effects (script step 8)

← back to top

For the next part, we have a catch-22 situation (i.e., a paradoxical situation)! To derive effective time-dependent corrections, we need to average both amplitude and phase in frequency. However, to average in frequency, the phase must be flat in time, and the amplitude must exhibit the correct spectral index!

To approach this, we derive initial time-dependent solutions for the bandpass calibration sources but discard them after applying them to derive the initial bandpass solutions. These solutions are then replaced in step 11.

3C i. Time-dependent pre-calibration to prepare for bandpass calibration

← back to top

Estimate the time-averaging interval for phase by plotting phase versus time for a single channel near the centre of the band using a bandpass calibration source. If the results for the first channel and antenna you try look poor, it may be a partially flagged channel; consider trying a different one. 

	plotms(vis='all_avg.ms',
		   field='**',    # Plot bandpass calibrator
		   spw='0~3:**', correlation='**'  # This gives all spw, choose channel in centre of spw in each and one correlation
		   antenna='**',  # Plot the longest baseline to the refant, likely to have the fastest-changing phase
		   xaxis='time', yaxis='phase',ydatacolumn='data', # Plot raw phase against time, no averaging
		   coloraxis='spw',plotfile='',
		   showgui=gui,
		   overwrite=True)

Zoom in to help determine which phase solution interval to use. The integration-to-integration scatter is mostly instrumental noise that cannot be removed, while the longer-term wiggles are primarily due to the atmosphere.

We aim to derive corrections to minimise these to about the level of the noise or to less than 5-10 degrees. The longer the solution interval, the better the signal-to-noise ratio (S/N), but the interval must be short enough to avoid averaging out the fluctuations. To illustrate this, we have taken the phase fluctuations on spectral window 0, channel 55, and utilised different averaging intervals. This reflects the approximate solutions we would obtain when calculating the phases.

As you can see, the various solution intervals will track the long-term slopes fairly effectively; however, the short 60-second wiggles are only effectively tracked by the 30-second solution interval. If we used the greater than 60-second intervals, we would still have errors of approximately 20 degrees, whereas with the 30-second intervals, the residuals will be closer to 5 degrees.

QUESTION 4: What other effects, aside from atmospheric phase errors, are addressed by calibrating the phase against a point model at the phase centre? Answer The origin of the phase is initially arbitrary and differs for each spectral window. The phase of a point source at the phase centre is flat at zero, so calibration should also align all the phases near zero while eliminating the wiggles.

Let's continue. By using the solution interval, which can track the wiggles, we want to derive the phase solutions with the task gaincal: 

	os.system('rm -rf bpcals_precal.p1')
	gaincal(vis='all_avg.ms',
		    calmode='**',
		    field='**',
		    caltable='bpcals_precal.p1',
		    solint='**',
		    refant='**',
		    minblperant=2,
		    gaintable='all_avg.K',
		    minsnr=2)

Check the solutions. Each spectral window should contain a coherent set of solutions, not merely noise. 

	plotms(vis='bpcals_precal.p1',
		   gridcols=3, gridrows=2,
		   xaxis='**',
		   yaxis='**',
		   plotrange=[-1,-1,-180,180],
		   iteraxis='antenna',
		   coloraxis='spw',
		   plotfile='bpcals_precal.p1.png')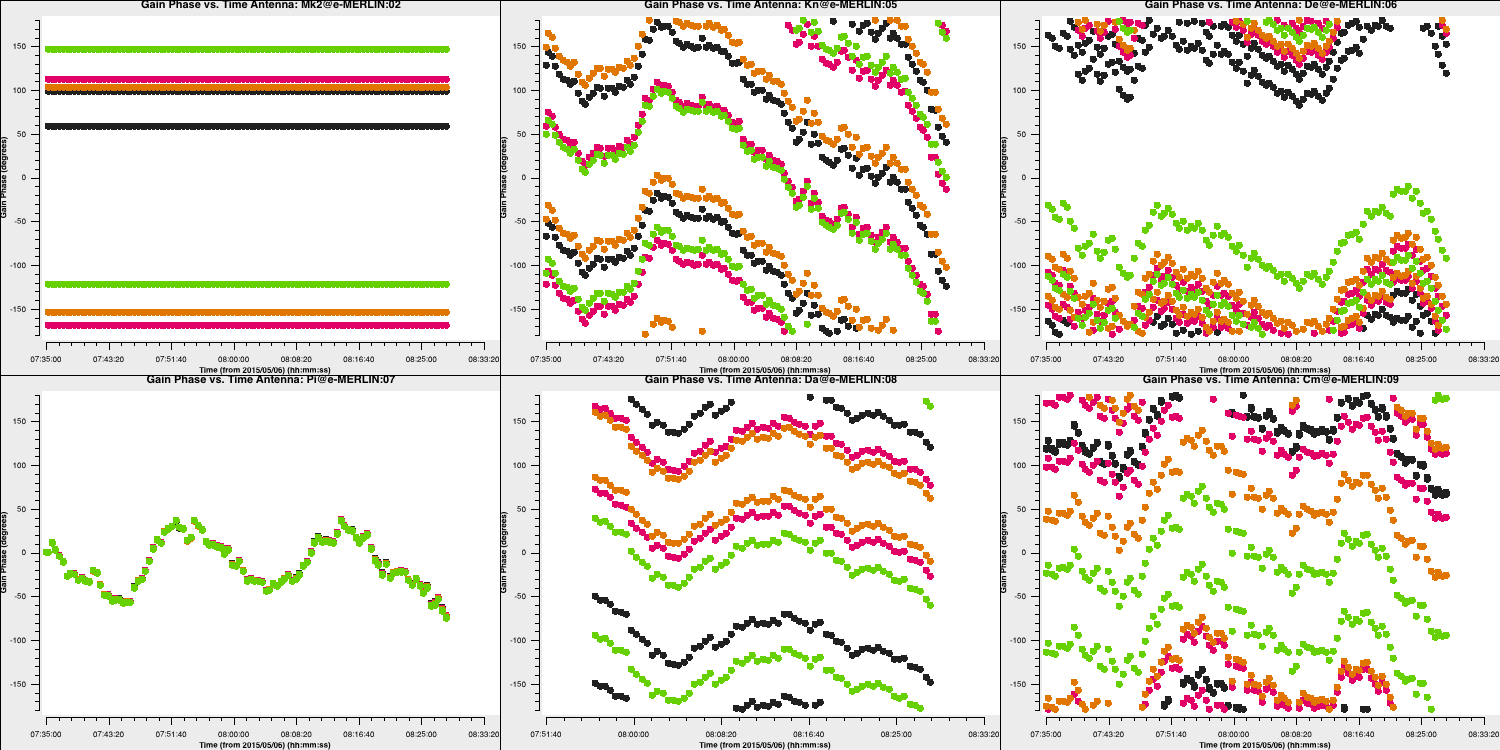

Note that the above plot focuses on 0319+415 to allow for clear observation of the phase solutions. The amplitude versus time plot in Step 6 also indicated that the uncorrected amplitudes exhibit only a gradual systematic slope over time, allowing for a longer solution interval that minimises phase noise.

QUESTION 5: Why should we solve for phase separately before solving for amplitude? AnswerThe phase errors change on timescales of less than a minute, while the amplitude drifts more slowly over time. Applying phase solutions derived every 30 seconds allows the data to be averaged into longer solution intervals, which improves the signal-to-noise ratio when deriving amplitude solutions.

Next, we need to derive amplitude solutions. We have not yet calculated flux densities for the bandpass calibration sources, so we must normalise the gains (i.e., individual solutions differ, but the product is unity, ensuring that the overall flux scale remains unaffected). Therefore, we need to derive the solutions separately for each of the two bandpass calibrators while writing them to the same solution table. 

	os.system('rm -rf bpcals_precal.ap1')
	gaincal(vis='all_avg.ms',
			field='0319+415',                # First bpcal
			caltable='bpcals_precal.ap1',    # Output solution table
			calmode='**',                    # Solve for amplitude and phase v. time
			solint='**',                     # Longer solution interval
			solnorm='**',                    # Normalise the amplitude solutions,
			refant='Mk2',
			minblperant=2,
			minsnr=2,
			append=False,
			gaintable=['all_avg.K','bpcals_precal.p1']) # Apply the existing delay and phase solutions

	gaincal(vis='all_avg.ms',
			field='1407+284',                # First bpcal
			caltable='bpcals_precal.ap1',    # Output solution table
			calmode='**',                    # Solve for amplitude and phase v. time
			solint='**',                     # Longer solution interval
			solnorm='**',                    # Normalise the amplitude solutions,
			refant='Mk2',
			minblperant=2,
			minsnr=2,
			append=True,
			gaintable=['all_avg.K','bpcals_precal.p1']) # Apply the existing delay and phase solutions

Alternatively, if you are doing this in the CASA prompt, you can enter the parameters for the first source and then simply adjust the field and append parameters.

Let's examine the solutions in plotms: 

	plotms(vis='bpcals_precal.ap1',
		   gridcols=3, gridrows=2,
		   xaxis='time',
		   yaxis='amp',
		   iteraxis='antenna',
		   coloraxis='spw',
		   plotfile='')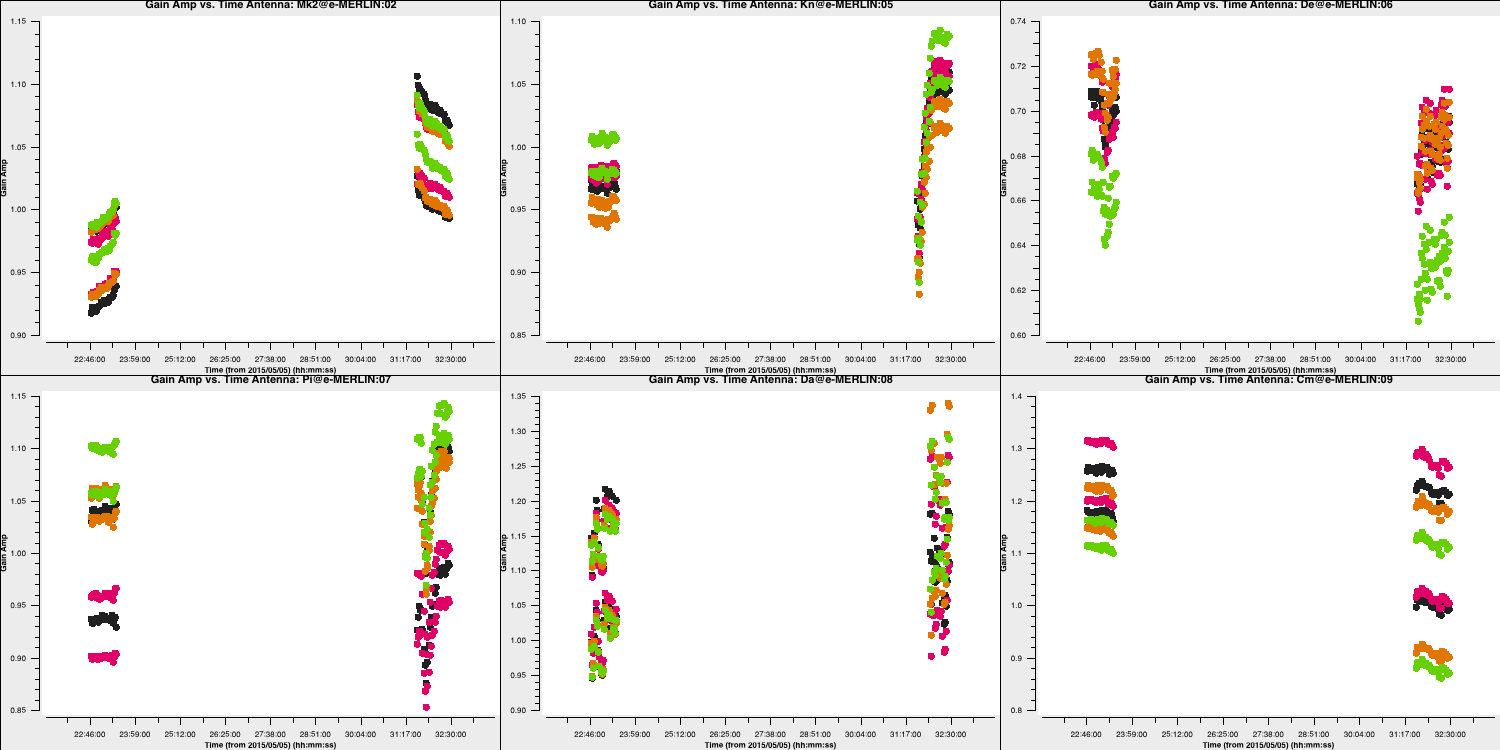

3C ii. Bandpass calibration

← back to top

Use bandpass to calculate solutions for phase and amplitude as functions of frequency (i.e., per channel). To enable time averaging, apply the time-dependent corrections that you have just derived. 

	os.system('rm -rf bpcal.B1')
	bandpass(vis='all_avg.ms',
			 caltable='bpcal.B1',         # New table with bandpass solutions
			 field='**,**',               # Bandpass calibration sources
			 fillgaps=16,                 # Interpolate over flagged channels
			 solint='inf',combine='scan', # Average the whole time for each source
			 solnorm='**',                # Normalise solutions
			 refant='**',
			 bandtype='B',
			 minblperant=2,
			 gaintable=['all_avg.K','bpcals_precal.p1','bpcals_precal.ap1'], # Apply all the tables derived for these sources
			 minsnr=3)

You may see messages about unsuccessful solutions, but these should all pertain to the end channels that were flagged regardless.

Check the solutions in plotms. The phase corrections are minor since the delay and phase solutions have already been applied. The amplitude solutions aim to eliminate local deviations from the bandpass, but the corrections so far assume that the source flux density is uniform in each spectral window.

Firstly, let's check phases: 

	plotms(vis='bpcal.B1',
		   gridrows=2, gridcols=3,
		   xaxis='**', yaxis='**', # Plot phase solutions v. frequency
		   plotrange=[-1,-1,-180,180],
		   iteraxis='antenna',
		   coloraxis='spw',
		   plotfile='')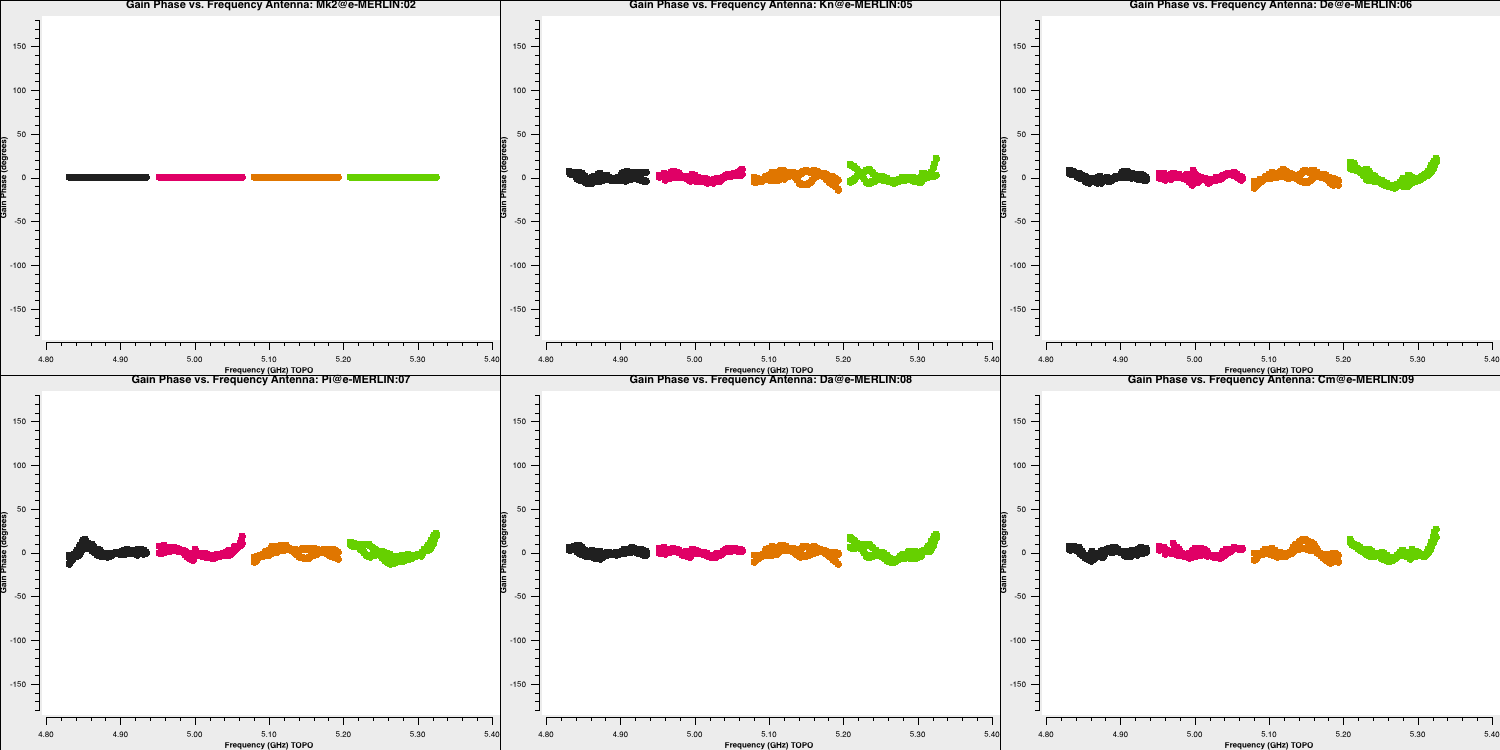

And then the amplitude solutions: 

	plotms(vis='bpcal.B1',
		   gridrows=2, gridcols=3,
		   xaxis='**', yaxis='**', # Plot amp solutions v. frequency
		   iteraxis='antenna',
		   coloraxis='spw',
		   plotfile='')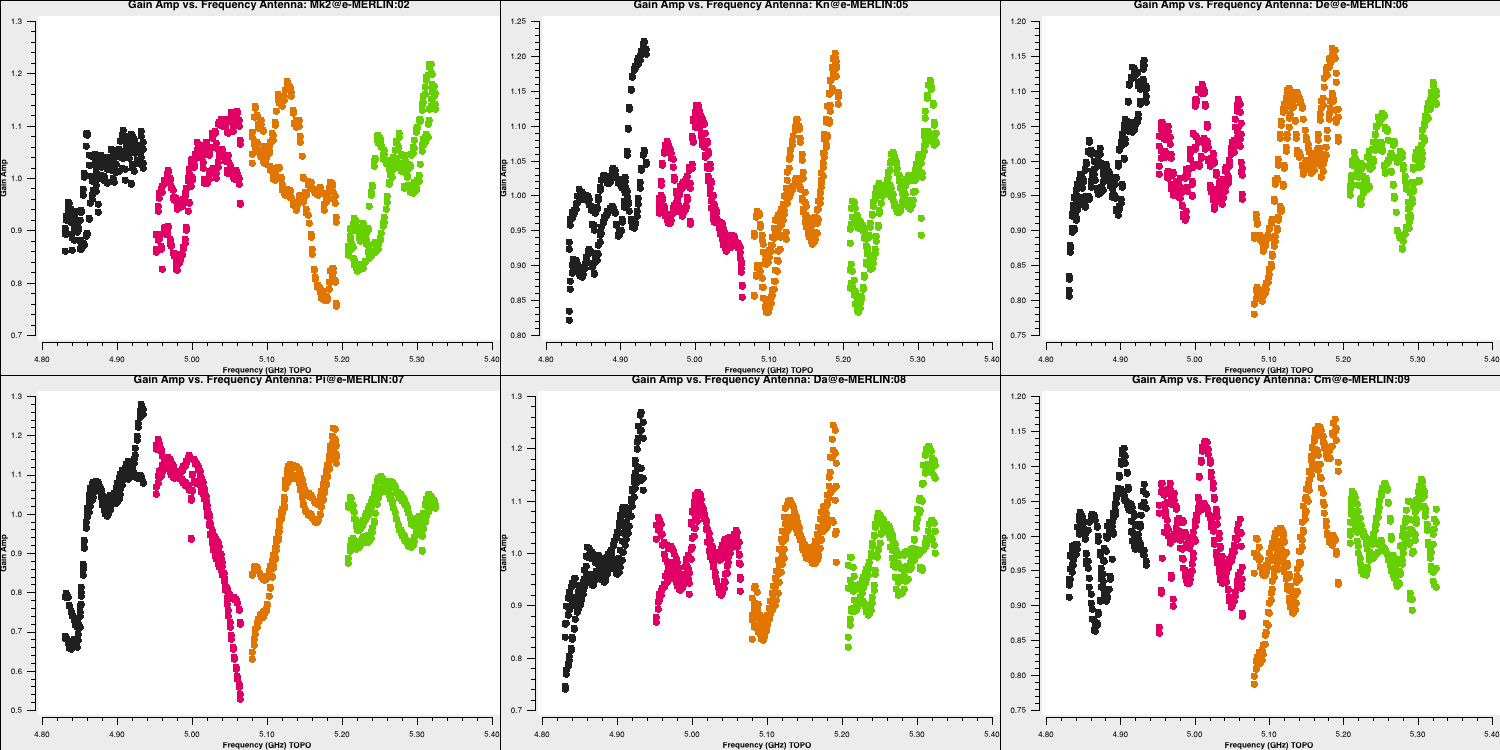

Apply the delay and bandpass solutions to the calibration sources as a test to ensure they effectively produce a flat bandpass for the phase reference. There is no need to implement the time-dependent calibration yet, as we have not derived this for the phase reference source.

Some notes about the task applycal:

  • The first time applycal is run, it creates the $\texttt{CORRECTED}$ data column in the measurement set. This can be quite slow.
  • Each time applycal is run, it replaces the entries in the $\texttt{CORRECTED}$ data column, i.e. the corrected column is not cumulative, but you can give applycal a cumulative list of gain tables.
  • applymode can be used to flag data with failed solutions but we do not want that here as this is just a test.
  • The interp parameter can take two values for each gaintable to be applied, with the first determining interpolation in time and the second in frequency. The times of data that need correction may coincide with, or be bracketed by, the times of calibration solutions. In this situation, linear interpolation can be used as the default, which is typically applied when using solutions derived from a source to itself or from phase ref to target in alternating scans. However, if solutions need to be extrapolated in time from one source to another that are not interleaved, then nearest is used. Similar reasoning applies to frequency. There are additional modes not covered here (see help applycal).

The delay correction ('K') table includes entries for all sources except the target. The phase reference scans bracket the target scans, so it is acceptable to use the default 'linear' interpolation.

The bandpass ('B1') table is derived from only two bandpass calibration observations, and there may be data for other sources beyond these times. Thus, extrapolation in time is necessary, using 'linear'. 'linear' interpolation is acceptable for the bandpass calibrator in frequency.

If you find that your laptop is slow, you can skip the applycal and the plotms immediately after, and simply look at the figures here before proceeding to step 9. 

	applycal(vis='all_avg.ms',
			 field='0319+415,1302+5748,1331+305,1407+284',
			 calwt=False,
			 applymode='calonly',   # So we don't change the weights or flag data with failed solutions
			 gaintable=['**','**'], # Enter the names of the tables used to calibrate the bandpass
			 interp=['**','**,**']) # The values depend on which table you listed first.

Verify that the bandpass corrections are adequate for all data by plotting the 'before and after' phase reference phase and amplitude against frequency. First, let's examine the uncorrected phase (in the interactive CASA prompt this time). 

# In CASA:
default(plotms)
vis='all_avg.ms'; field='1302+5748'                 # Phase reference
xaxis='frequency';yaxis='phase';ydatacolumn='data'  # First, plot uncorrected phase
gridrows=5;gridcols=1;avgtime='600';coloraxis='scan'
iteraxis='baseline';antenna='Mk2&*';correlation='LL,RR'
plotms()

And next, the corrected phase: 

ydatacolumn='corrected'
plotms()

Then, the uncorrected amplitude: 

yaxis='amp'
ydatacolumn='data'
plotms()

And finally, the corrected amplitude: 

ydatacolumn='corrected'
plotms()

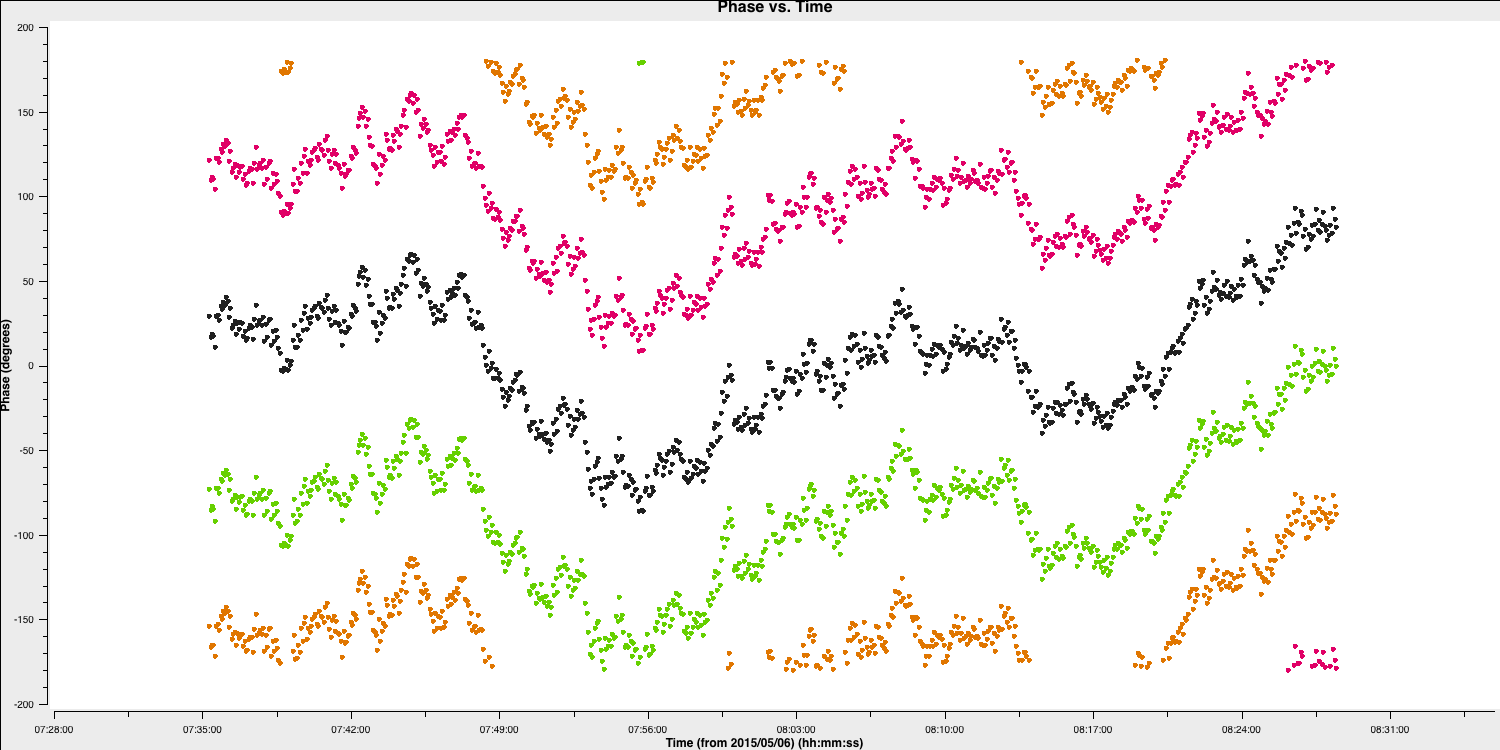
The scripted versions of these commands are included in the 3C277.1_cal_outline.py script, specifically between lines 464-508. The plot below displays the uncorrected and corrected amplitudes and phases for the Mk2-Cm baseline of the phase reference source (1302+5748), which are colour-coded by scan. For clarity, it has been replotted in Python below.

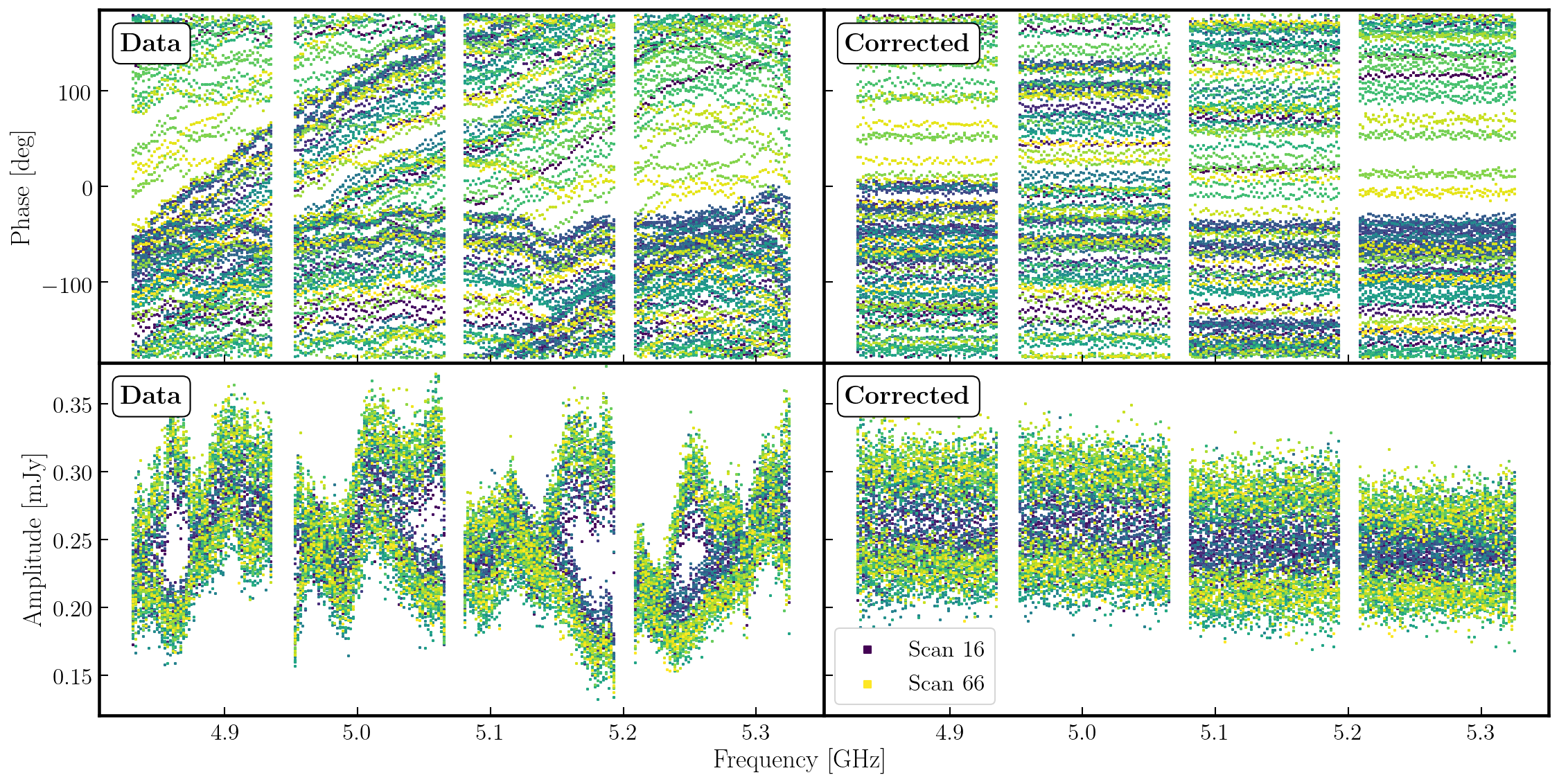
In the figure, each scan is coloured separately, showing a random phase offset and some discrepancies in amplitude compared to other scans. However, for each individual time interval, it remains quite flat. Therefore, we can average the frequency across each spectral window and plot the data to illustrate the remaining time-dependent errors.

Plot the corrected phase against time, averaging all channels for the phase reference source. Zoom in on several scans to determine an appropriate averaging timescale for correcting phase errors as a function of time, specifically where atmospheric fluctuations dominate over noise. Additionally, we will use the interactive CASA prompt. 

# In CASA:
default(plotms)
vis='all_avg.ms'; field='1302+5748'
xaxis='time';yaxis='phase';ydatacolumn='corrected'
antenna='Mk2&*';iteraxis='baseline'
avgchannel='64'; coloraxis='spw'
correlation='LL'    # Just one pol as previous plots show both are similar
plotms()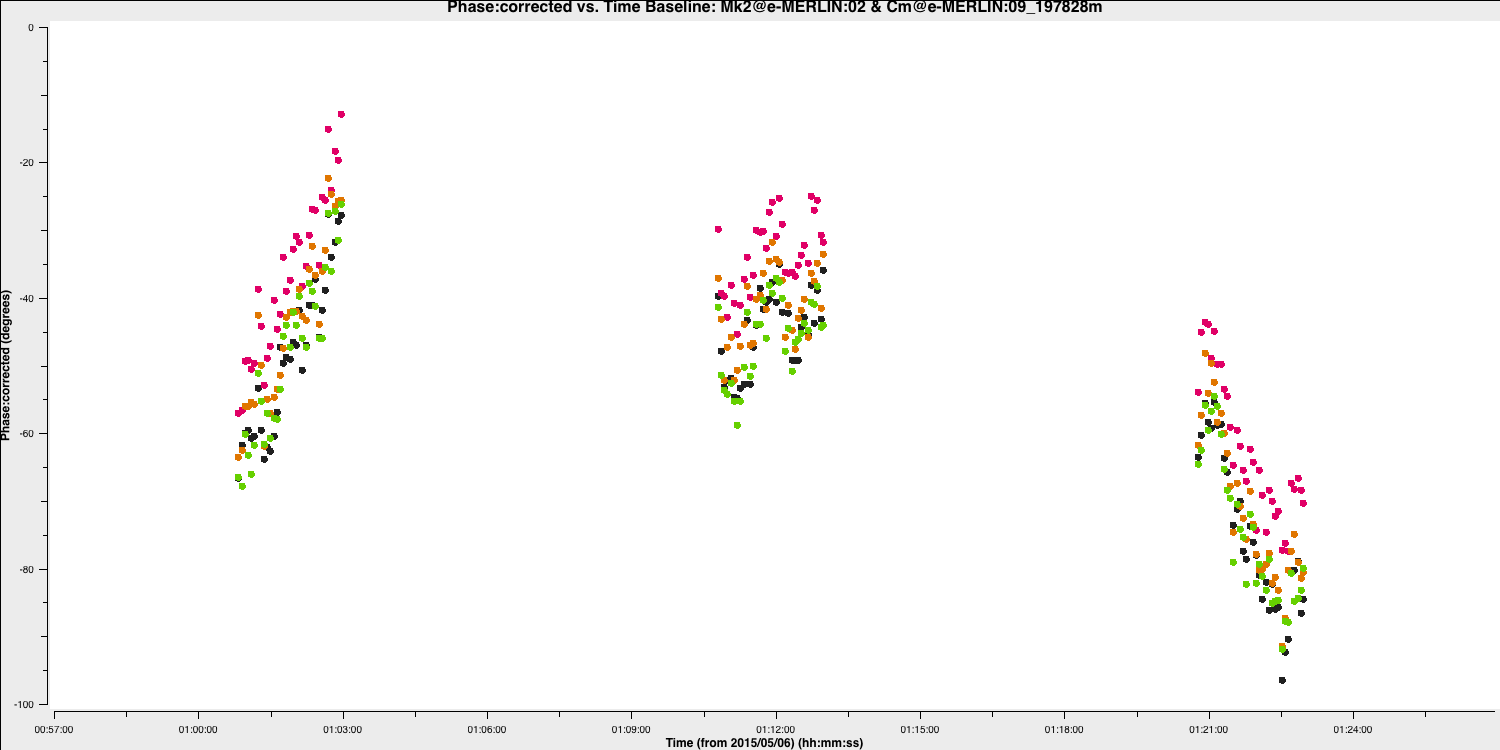

And repeat for amplitudes:

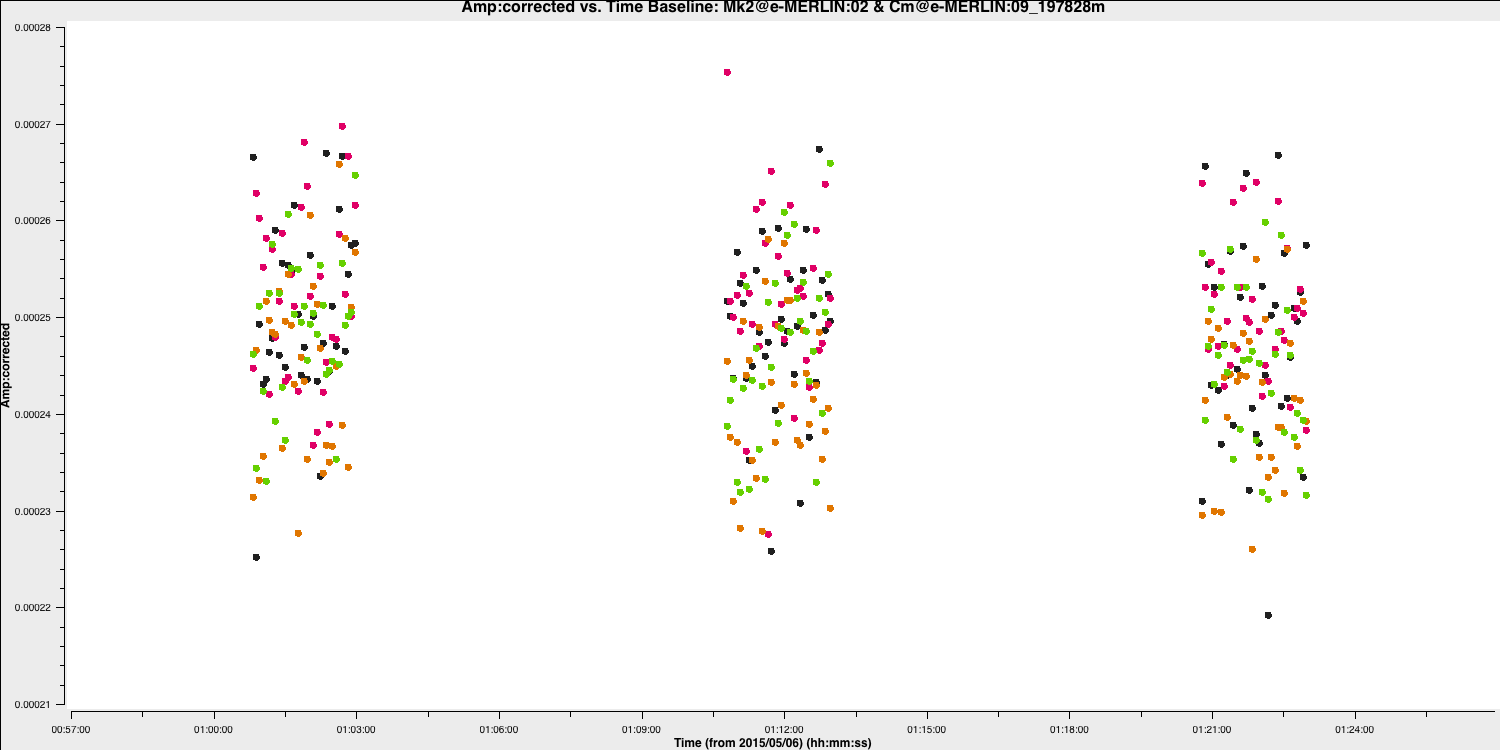
3D. Gain calibration (script step 9)

3D i. Time-dependent phase calibration of all calibration sources

← back to top

	gaincal(vis='all_avg.ms',
			calmode='p',              # Phase only first
			caltable='calsources.p1',
			field='**',               # All calibration sources
			solint='**',              # Insert solution interval
			refant=antref,
			minblperant=2,minsnr=2,
			gaintable=['all_avg.K','bpcal.B1'], # Existing correction tables to apply
			interp=['**','**,**'])              # Insert suitable interpolation modes

When you run gaincal, check the messages in the logger and the terminal. The logger shows something like: 

2025-03-26 08:16:44	INFO	calibrater::solve	Finished solving.
2025-03-26 08:16:44	INFO	gaincal::::casa	Calibration solve statistics per spw:  (expected/attempted/succeeded):
2025-03-26 08:16:44	INFO	gaincal::::casa	  Spw 0: 1400/935/930
2025-03-26 08:16:44	INFO	gaincal::::casa	  Spw 1: 1400/935/930
2025-03-26 08:16:44	INFO	gaincal::::casa	  Spw 2: 1400/935/930
2025-03-26 08:16:44	INFO	gaincal::::casa	  Spw 3: 1400/935/930
2025-03-26 08:16:46	INFO	gaincal::::casa	Task gaincal complete. Start time: 2025-03-26 11:15:28.580148 End time: 2025-03-26 11:16:46.359460

This means that although there are 1,400 16s intervals in the calibration source data, about a third ($1400- 935 = 465$) of them have been partly or totally flagged. However, almost all ($99.4\%$) of the intervals that contain sufficient unflagged ('attempted') data produced good solutions ('succeeded'). There are no additional messages regarding completely flagged data, but in the terminal, you will see a few notifications when there are fewer than the requested 2 unflagged baselines per antenna: 

Insufficient unflagged antennas to proceed with this solve.
(time=2015/05/06/06:32:26.5 field=0 spw=0 chan=0)

Here, there are very few predictable failures. If there are many or unexpected failures, investigate - perhaps there are unflagged bad data, pre-calibration has not been applied, or an inappropriate solution interval has been used.

Next, we can plot the solutions separately for L and R to enhance clarity: 

	plotms(vis='calsources.p1',
		   gridrows=2, gridcols=3,
		   xaxis='time',
		   yaxis='phase',
		   plotrange=[-1,-1,-180,180],
		   iteraxis='antenna',
		   coloraxis='spw',
		   correlation='L', # Note that solutions are per antenna, hence 'L' not 'LL'
		   plotfile='')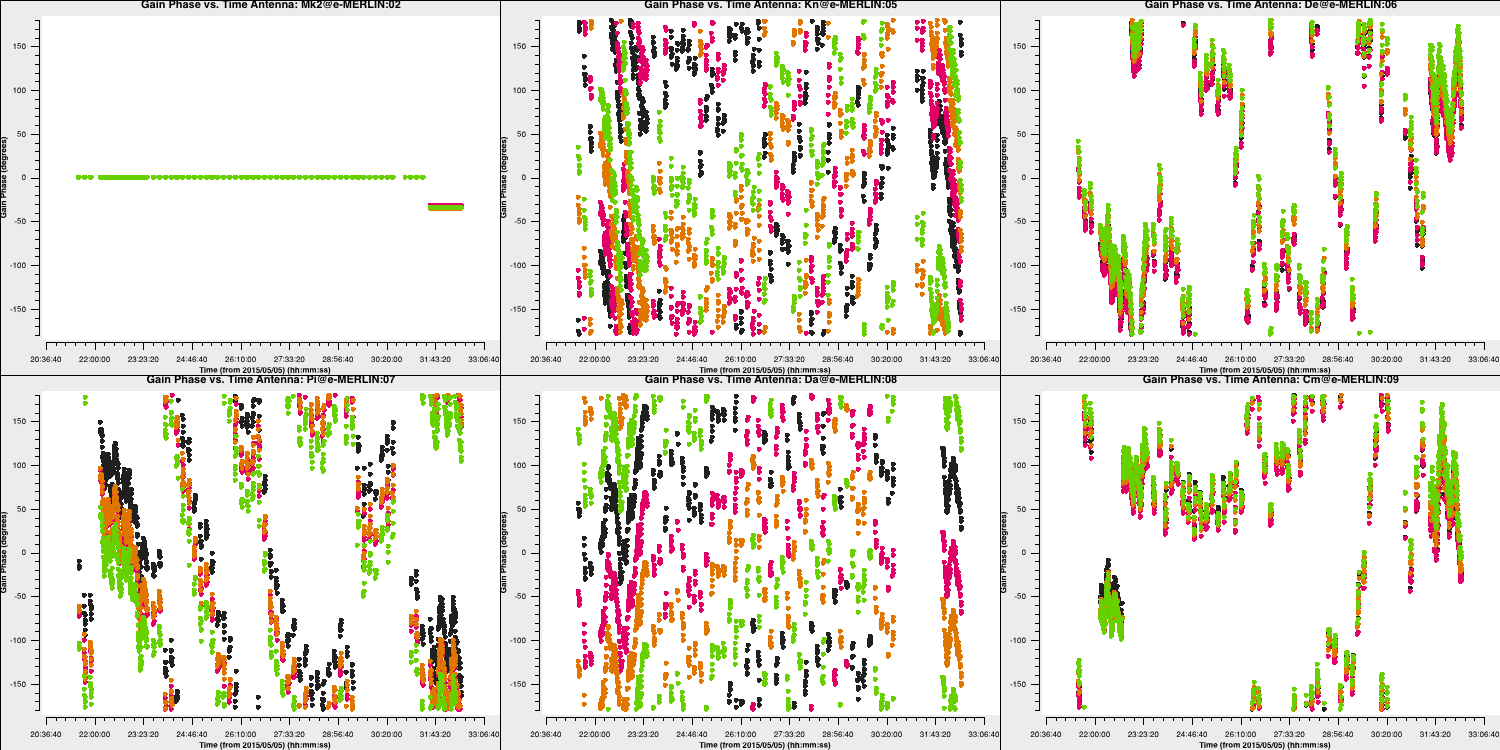

The phase corrections exhibit a similar time dependence to that of the uncorrected data phase and are not random; if they appear to be just noise, something is amiss.

3D ii. Time-dependent amplitude calibration of all calibration sources

← back to top

Now we can derive time-dependent solutions for all calibration sources, using the delay and bandpass tables along with the time-dependent phase solution table.

At this point, 1331+305 has a realistic model set in the measurement set (Step 7). The other calibration sources default to a 1 Jy point source at the phase centre. If (and only if) you are repeating a failed attempt, reset any previous models for sources other than 1331+305. 

# In CASA:
default(delmod)
vis='all_avg.ms'
field='0319+415,1407+284,1302+5748,1252+5634'
delmod()

Insert a suitable solution interval based on the inspection of the previous amplitude plots and the output from listobs, along with the tables to apply and interpolation modes. Keep in mind that if you set a solution interval longer than a single scan for a source, the data will still only be averaged within each scan unless an additional 'combine' parameter is set, which is not needed in this case. 

	gaincal(vis='all_avg.ms',
			calmode='ap',               # Amplitude and phase
			caltable='calsources.ap1',
			field='**',                 # All calibration sources
			solint='**',                # Insert solution interval.
			solnorm=False,              # Solutions will be used to determine the flux scale - don't normalise!
			refant='Mk2',
			minblperant=2,minsnr=2,
			gaintable=['all_avg.K','bpcal.B1','calsources.p1'],
			interp=['**','**,**','**']) # Insert suitable interpolation modes

The logger displays a similar ratio of expected to attempted solution intervals as it does for phase; however, those with failed phase solutions are not attempted, so all attempted solutions are successful.

Plot the solutions for L and R separately for clarity: 

	plotms(vis='calsources.ap1',
		   gridrows=2, gridcols=3,
		   xaxis='time',
		   yaxis='amp',
		   iteraxis='antenna',
		   coloraxis='spw',
		   correlation='L',
		   plotfile='')

	plotms(vis='calsources.ap1',
		   gridrows=2, gridcols=3,
		   xaxis='time',
		   yaxis='amp',
		   iteraxis='antenna',
		   coloraxis='spw',
		   correlation='R',
		   plotfile='')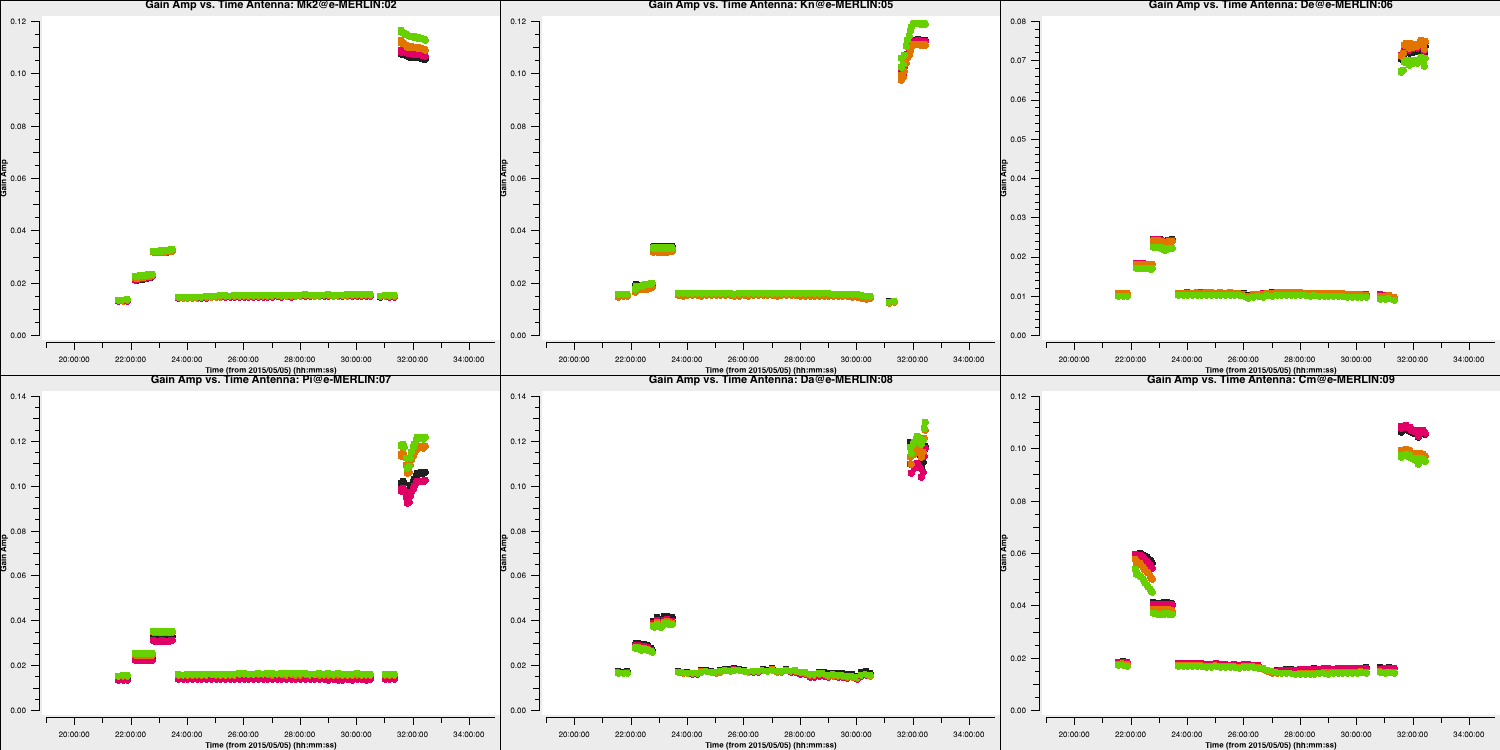

The plot above shows the time-dependent amplitude solutions for the L polarisation, coloured by spectral window. The solutions for each individual source appear similar, but there are significant differences between sources. All have been compared with a 1 Jy point source model, except for 1331+305, yet they possess different flux densities.

3E. Determining flux densities of calibration sources (script step 10)

3E i. Derive calibrator flux densities

← back to top

The solutions for 1331+305 in calsources.ap1 contain the correct scaling factor to convert the raw units coming from the correlator to physically realisable units (i.e., Janskys) while also removing time-dependent errors. This scaling factor is used to calibrate the other calibration sources in the CASA task fluxscale. We run this task differently because the calculated fluxes are returned in the form of a Python dictionary and are also written to a text file. Only the best data are used to derive the flux densities, but the output remains valid for all antennas. This method assumes that all sources without starting models are point sources, so it cannot be used for an extended target. 

	os.system('rm -rf calsources.ap1_flux calsources_flux.txt')
	calfluxes=fluxscale(vis='all_avg.ms',                # calfluxes will hold the calculated fluxes in memory
						caltable='calsources.ap1',       # Input table containing amplitude solutions
						fluxtable='calsources.ap1_flux', # Scaled output table
						listfile='calsources_flux.txt',  # Text file on disk listing the calculated fluxes
						gainthreshold=0.3,               # Exclude solutions >30% from mean
						antenna='!De',                   # Exclude least sensitive antenna
						reference='1331+305')            # Source with known flux density and previous model

If you type calfluxes into the CASA prompt, this will display the Python dictionary. However, if you're not yet familiar with parsing it, check the logger or the listfile calsources_flux.txt using: 

!more calsources_flux.txt       # Use of ! to invoke shell command

The estimates for individual spectral windows may have uncertainties of up to $\sim20\%$, but the final three lines provide the fitted flux density and spectral index for all spectral windows, which should be accurate to within a few percent. These fluxes require an additional scaling factor of $0.938$ to account for the resolving out of 1331+305 by the long e-MERLIN baselines (see Setting the flux of the primary flux scale calibrator, step 7). The Python dictionary calfluxes is used for this scaling. 

	eMcalfluxes={}
	for k in calfluxes.keys():
		if len(calfluxes[k]) > 4:
			a=[]
			a.append(calfluxes[k]['fitFluxd']*0.938)
			a.append(calfluxes[k]['spidx'][0])
			a.append(calfluxes[k]['fitRefFreq'])
			eMcalfluxes[calfluxes[k]['fieldName']]=a

This creates a new Python dictionary called eMcalfluxes, which we can print using print(eMcalfluxes) to produce: 

{'1302+5748': [0.4043422839021926, -0.3654536785314739,  5069980155.629359],
 '1407+284':  [1.9012873926908314,  0.30684493005193103, 5069980155.629359],
 '0319+415':  [22.931908094424525,  1.3882373541791695,  5069980155.629359]}

where the first column, or 'key', represents the source name, and the values are [flux density (Jy), spectral index, and reference frequency (Hz)]. You may observe slightly different values if you select different solution intervals; however, if they differ by more than a few percent, something is likely wrong.

3E ii. Setting the calibrator flux densities

← back to top

If you exit and restart CASA before running this step, you will need to re-define eMcalfluxes by copying the three lines that begin with eMcalfluxes = ... into the CASA prompt.

Next, we will use setjy in a loop to set each calibration source’s flux densities. The logger will report the values being set. 

	for f in eMcalfluxes.keys(): # For each source in eMcalfluxes:
		setjy(vis='all_avg.ms',
			  field=f,
			  standard='manual',          # Use our values, not a built-in catalogue
			  fluxdensity=eMcalfluxes[f][0],
			  spix=eMcalfluxes[f][1],
			  reffreq=str(eMcalfluxes[f][2])+'Hz')

The default in setjy scales by the spectral index for each channel, and plotting the models for the bandpass calibrators reveals a slope corresponding to the spectral index (zoom in on the fainter source to observe this). Both sources exhibit positive spectral indices in this frequency range; this is less unusual for compact, bright QSOs than for radio galaxies in general.

Plot the models for the bandpass calibrators, with amplitude plotted against frequency, to observe the spectral slopes. 

	plotms(vis='all_avg.ms', field='0319+415,1407+284',   # Plot the bandpass calibrators
		   xaxis='***',
		   yaxis='***',ydatacolumn='***',      # Fill in axis and data types
		   coloraxis='spw',correlation='LL',   # Just LL for speed; model is unpolarised
		   symbolsize=5, customsymbol=True, 
		   symbolshape='circle',
		   plotfile='',overwrite=True)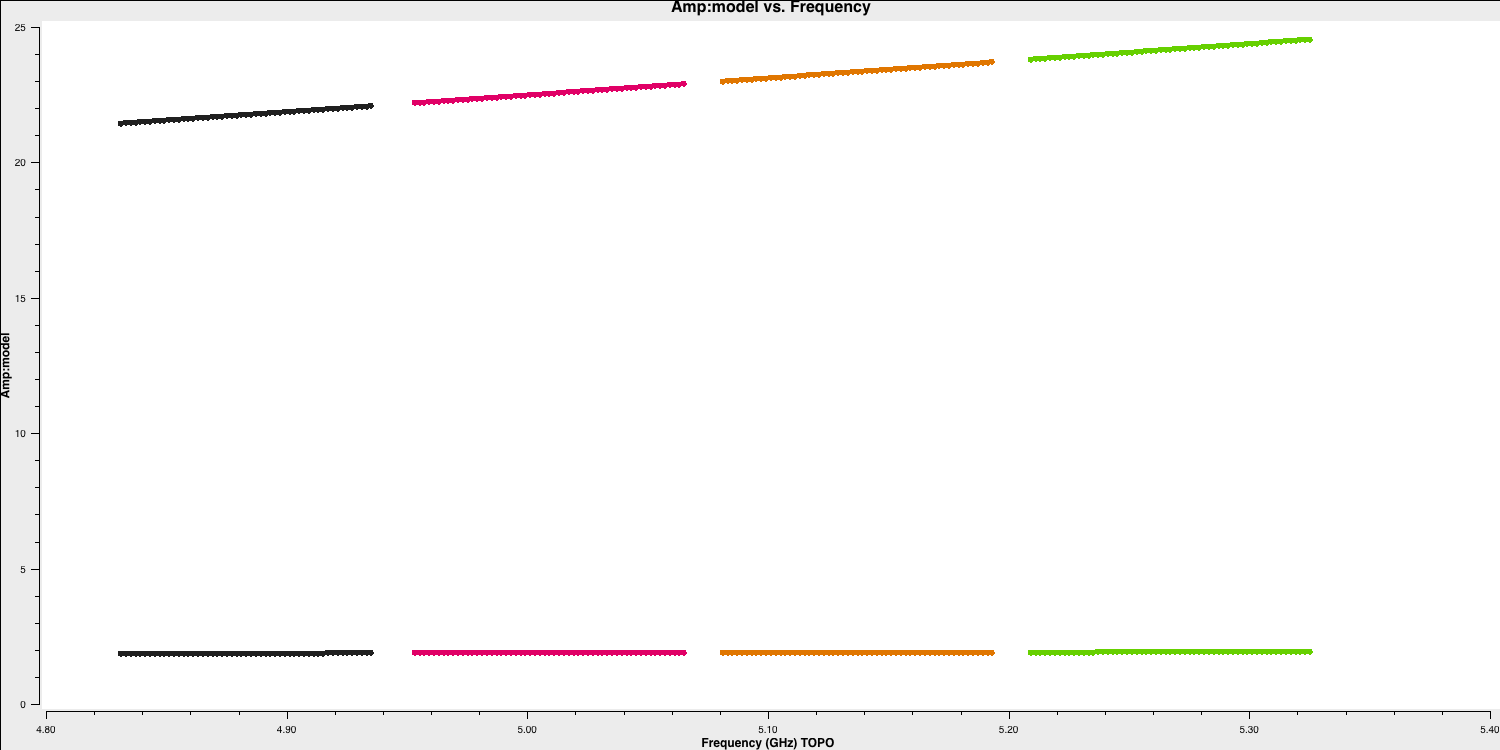

3F. Improved bandpass calibration (script step 11)

← back to top

In this step, we will use the models, including spectral indices, to derive a more accurate bandpass correction. You can refer to the initial use of bandpass as a guide, but there are three major differences (besides creating a different table). 

	os.system('rm -rf bpcal.B2')
	bandpass(vis='all_avg.ms',
		caltable='bpcal.B2',
		field='**,**',
		fillgaps=**,
		solint='**',combine='**',
		refant=antref,
		minblperant=2,
		solnorm='**',                      # There are now accurate flux densities and spectral indices so?
		gaintable=['all_avg.K','**','**'], # and updated time-dependent solutions
		gainfield='**,**',                 # but the new solutions contain entries for a number of sources
		minsnr=3)

Next, we aim to plot the solutions for both phase and amplitude: 

	plotms(vis='bpcal.B2',
		   gridrows=2, gridcols=3,
		   xaxis='freq', yaxis='phase', # Plot phase solutions v. frequency
		   plotrange=[-1,-1,-180,180],
		   iteraxis='antenna',
		   coloraxis='spw',
		   plotfile='')

	plotms(vis='bpcal.B2',
		   gridrows=2, gridcols=3,
		   xaxis='freq', yaxis='amp', # Plot amp solutions v. frequency
		   iteraxis='antenna',
		   coloraxis='spw',
		   plotfile='')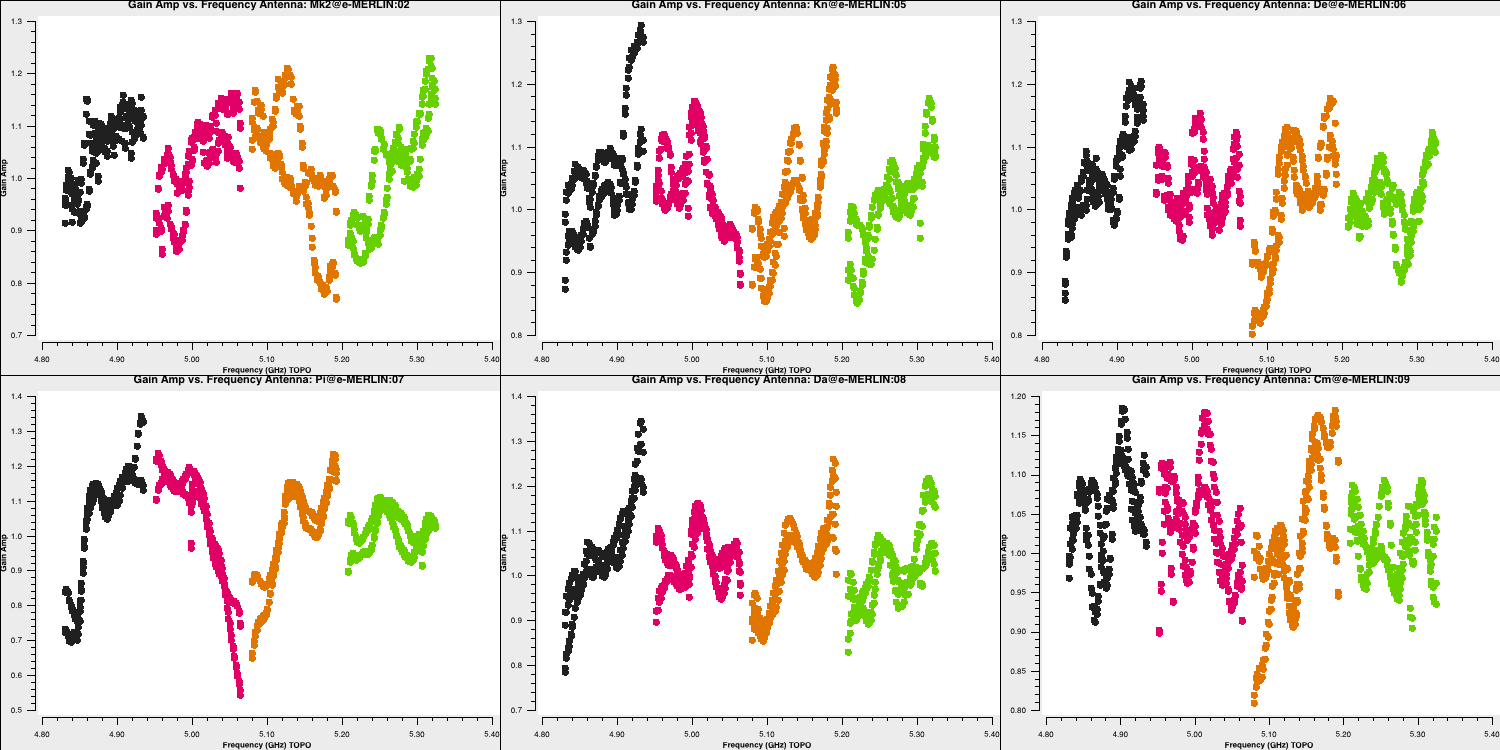

These solutions resemble the initial bandpass approximation but feature a different slope. To illustrate this, the initial bandpass and improved bandpass solutions for Knockin (Kn) are plotted below. You can observe the same wiggles as in B1, but with a different overall slope.

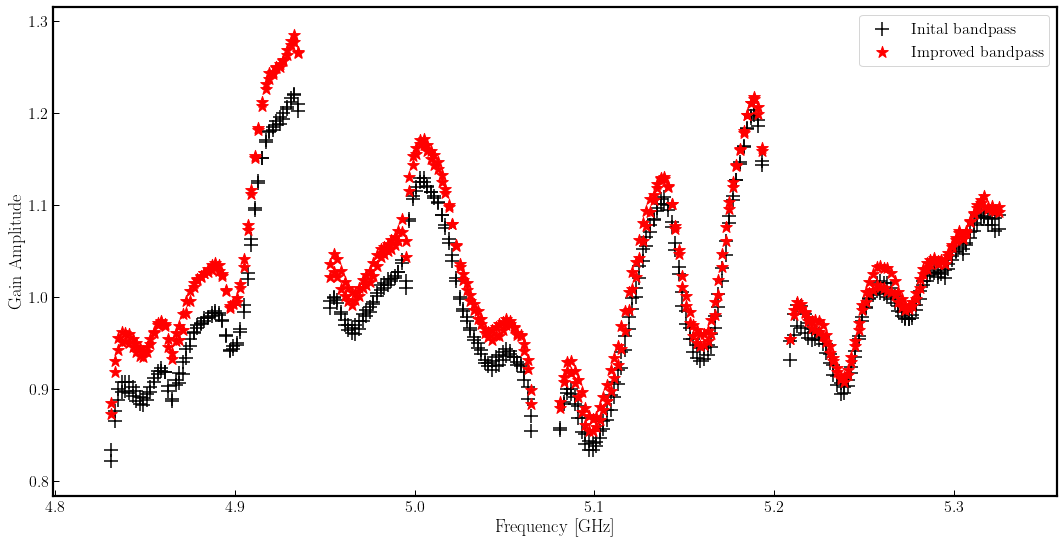
3G. Derive solutions for all cal sources with improved bandpass table (script step 12)

3G i. Derive amplitude solutions

← back to top

For each calibration source, there is now a flux density and spectral index assigned to the $\texttt{MODEL}$ column of the measurement set, along with the delay, phase, and enhanced bandpass calibration. These are used to derive time-dependent amplitude solutions that not only correct short-term errors but also provide an accurate flux scale factor.

Review the last time you ran gaincal, and identify what you need to change now (other than the output table name). 

	os.system('rm -rf calsources.ap2')
	gaincal(vis='all_avg.ms',
			calmode='ap',
			caltable='calsources.ap2',
			field='**',
			solint='**',
			refant='**',
			minblperant='**',minsnr='**',
			gaintable=['**','**','**'],
			interp=['**','**,**','**'])

Plot the solutions: 

plotms(vis='calsources.ap2',
		   gridrows=2, gridcols=3,
		   xaxis='time',
		   yaxis='amp',
		   iteraxis='antenna',
		   coloraxis='spw',
		   correlation='L',
		   plotrange=[-1,-1,0.01,0.06],
		   plotfile='') # repeat for other polarisation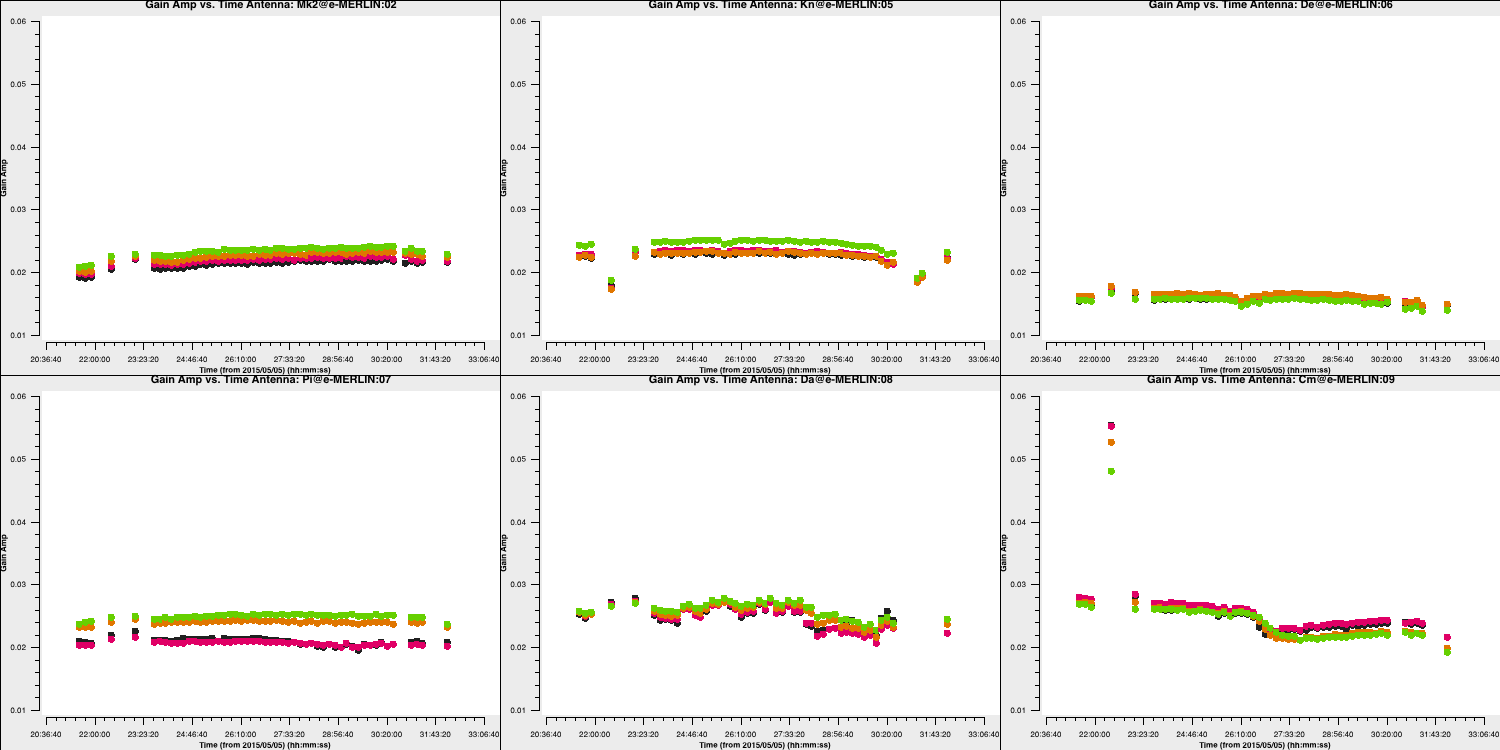

You can expect to see a similar scaling factor for all sources. The values for Cm (the antenna providing the longest baselines) are somewhat resolved for 1331+305, indicating slightly higher values.

3G ii. Derive scan-averaged phase solutions to be applied to the target source

← back to top

Finally, we need phase solutions that can be applied to the target source. Since we will interpolate solutions between phase calibrator scans, we only require one phase solution for each phase calibrator scan. Therefore, the solution interval should encompass all the data from each scan to create a solution. 

	os.system('rm -rf calsources.p2')
	gaincal(vis='all_avg.ms',
			calmode='**',
			caltable='calsources.p2',
			field='**',
			solint='**',
			refant='**',
			minblperant=**,minsnr=**,
			gaintable=['**','**'],
			interp=['**','**,**'])

And again, we should plot the solutions: 

	plotms(vis='calsources.p2',
		   gridrows=2, gridcols=3,
		   xaxis='time',
		   yaxis='phase',
		   iteraxis='antenna',
		   coloraxis='spw',
		   correlation='L',
		   plotrange=[-1,-1,-180,180],
		   plotfile='')

3H. Apply final calibrator source solutions and plot phase-ref and target (script step 13)

3H i. Apply solutions

← back to top

Apply the bandpass correction to all sources. For the other gaintables, the solutions for each calibrator (field) are applied to the same source (gainfield). A gainfield='' for the bandpass table means that solutions from all fields in that gaintable are applied. The applymode='calflag' will flag data with failed solutions, which is acceptable since we know that these failures were due to bad data. We use the non-interactive format to enable looping over all calibration sources.

Cut and paste this all together; press return a few times until it runs. 

cals = ['0319+415', '1302+5748', '1331+305', '1407+284']
for c in cals:
    applycal(vis='all_avg.ms',
             field=c,
             gainfield=[c, '',c,c],
             calwt=False,
             applymode='calflag',
             gaintable=['all_avg.K','bpcal.B2','calsources.p1','calsources.ap2'],
             interp=['linear','linear,linear','linear','linear'],
             flagbackup=False)                           # Don't back up flags multiple times here

Apply the phase referencing solutions to the target. We assume that the phase reference scans encompass the target scans, so linear interpolation is used, except for bandpass. Enter the parameters in interactive mode. 

	applycal(vis='all_avg.ms',
			 field='1252+5634',
			 gainfield=['**','','**','**'], # Enter the field whose solutions are applied to the target
			 calwt=False,
			 applymode='**',  # Not too many failed solutions - OK to flag target data
			 gaintable=['**','**','**','**'],
			 interp=['**','**,**','**','**'],
			 flagbackup=True)

3H ii. Plot phase-ref and target amplitudes against uv distance

← back to top

Next, we want to visualise our target and phase reference source. We need to ensure that the phase reference source is a true point source and determine if there is structure on the target. We can accomplish this by examining the amplitude versus $uv$ distance plots. Remember, a point source will appear flat with respect to $uv$ distance. 

	plotms(vis='all_avg.ms', field='1302+5748', xaxis='uvdist',
		   yaxis='amp',ydatacolumn='corrected',
		   avgchannel='64',correlation='LL,RR',
		   overwrite=True,
		   showgui=True,
		   coloraxis='spw')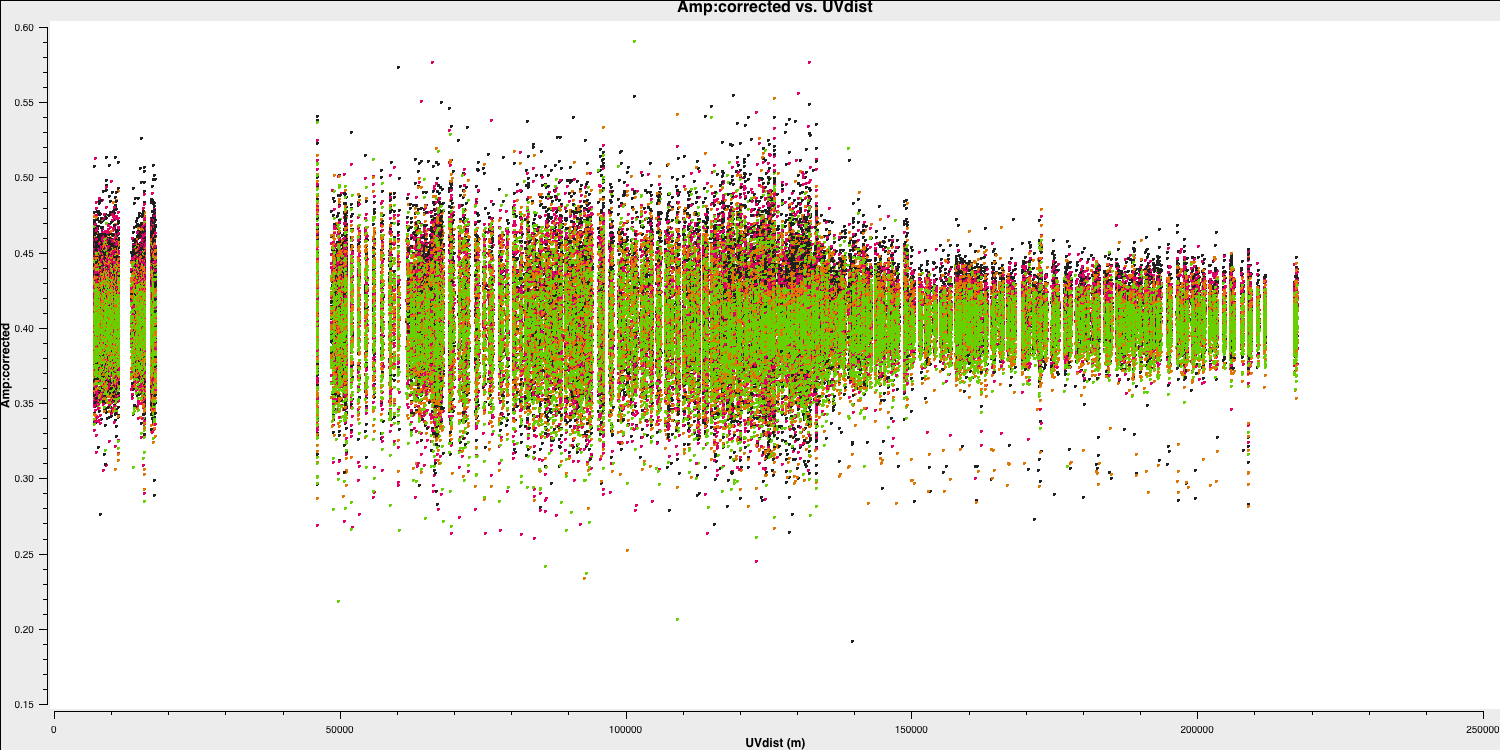

This looks pretty point-like!. Let's repeat the above for the target.

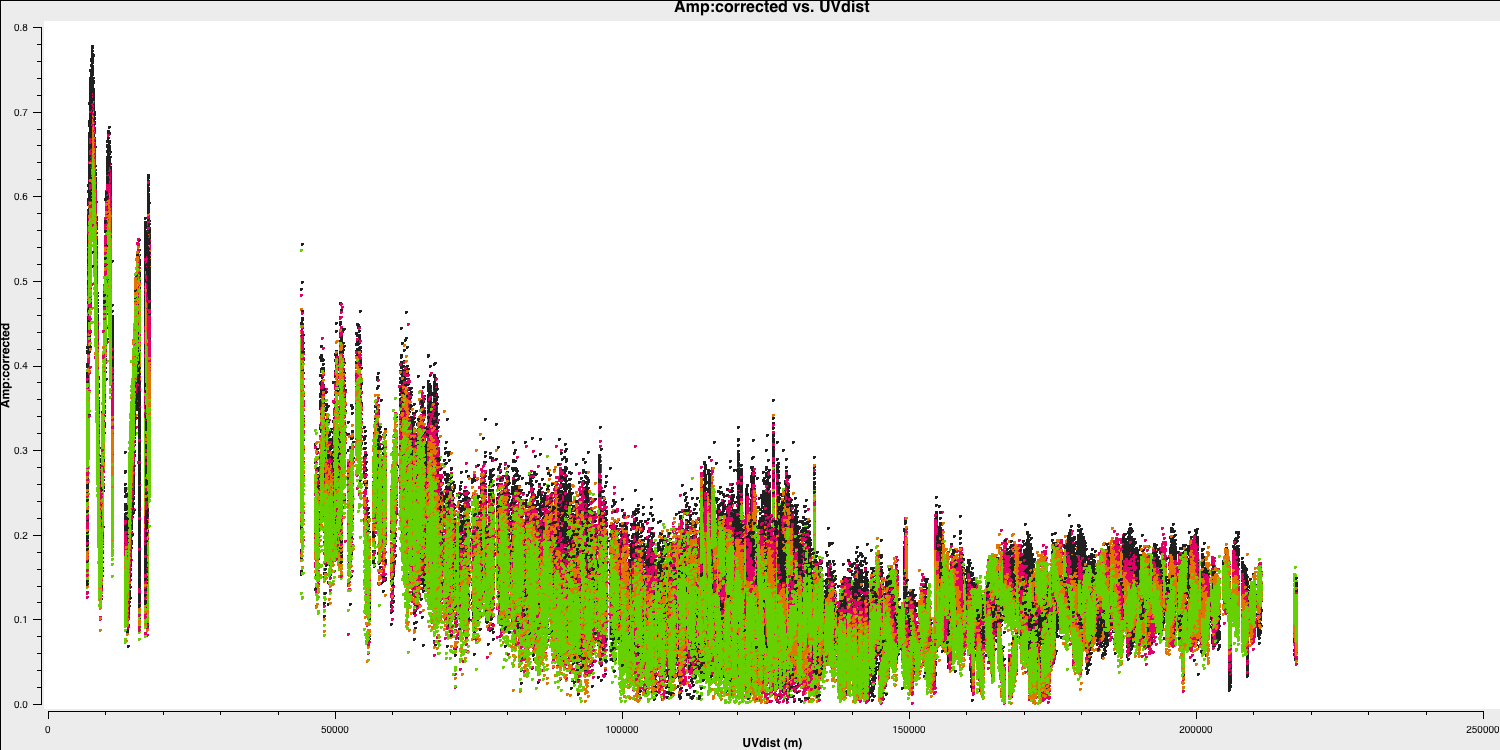
Hurray, there's some structure here!

QUESTION 6: What do the plots of amplitude against $uv$ distance tell you? Answer The visibility amplitudes for the phase reference are constant as a function of projected baseline length (uv distance in metres), indicating that it appears point-like at e-MERLIN resolutions.
The amplitudes are noisiest out to 130km, as these are the Defford baselines, which are less sensitive. There is some data that is anomalously low, but this is acceptable since the target is bright.
The target exhibits higher amplitudes on shorter baselines, suggesting that it has structure on scales larger than 50 mas and complex structure on the longer baselines.

3I. Split out target (script step 14)

← back to top

Extract the corrected target data. By default, this will use the corrected column. 

	os.system('rm -rf 1252+5634.ms*')
	split(vis='all_avg.ms',
		  field='1252+5634',
		  outputvis='1252+5634.ms',
		  keepflags=True)

Ensure you save 1252+5634.ms for the imaging stages in part 2 of this workshop.

Script with solutions

If you had problems in any of the steps, you should use the calibration script 3C277.1_cal_all.py

Continue with imaging tutorial

You are ready to image the target source using the splitted calibrated data in 1252+5634.ms

To part 2: Imaging of 3C277.1