5. Gravitational lenses and Hubble's constant
About Hubble's constant
When external galaxies were first identified and their optical spectra measured, it was found that the spectral lines of the galaxies did not appear at their expected places; instead, they were redshifted - that is, they appeared at longer wavelength than the expected wavelength of the line. This was interpreted as an overall recession of other galaxies from our own Galaxy. See this discussion from Strobel's notes.
In the 1920's Edwin Hubble, investigated this effect extensively for nearby galaxies using the telescopes of the Mount Wilson Observatory. [The Mount Wilson website also contains a picture of Hubble in action]. He discovered that the recession velocity of a galaxy, v, was proportional to its distance, d, according to Hubble's law:
v=H0d
where H0 is the Hubble constant. This law corresponds to an overall expansion of the Universe, in which every galaxy sees others receding according to the same law - Hubble's law. The recession is believed to have originated in a Big Bang about 10-20 billion years ago. Given that distances in extragalalactic astronomy are often measured in megaparsecs and velocities in kilometres per second, Hubble's law shows that the units of Hubble's constant are kms-1Mpc-1.
Show that the age of the universe is 1/H0,
assuming that the expansion has proceeded at constant velocity. If
|
The Hubble constant is obviously a very important number. It allows us to calculate a distance to a distant galaxy simply by knowing its redshift and hence its recession velocity. It is vital in cosmology. Yet it is difficult to measure, and until very recently it was poorly known, with different authors claiming values of between 50 and 90 kms-1Mpc-1. The conventional method of measurement, using a "distance ladder" of parallax, cluster fitting, Cepheid variables and type Ia supernovae, is cumbersome and subject to error, as each method is used to calibrate the one following it and the errors accumulate. Nevertheless, values of the Hubble constant have been calculated using this method (and substantial quantities of HST time), recently culminating in the HST Distance Scale Key Project's latest value of 72(+/-8)kms-1Mpc-1. However, the Hubble constant is such an important parameter that we need other methods of measurement, especially if the new methods are one-step independent determinations rather than the multi-step methods used in the past.
Gravitational lenses offer such an alternative and potentially cleaner method. The principle is as follows. First, suppose the background source is variable - i.e. it brightens and fades - and suppose that at a given time it undergoes a sudden brightening. This will of course mean that the observer will see each of the multiple images brighten.
However, the light paths which correspond to each of the multiple images will be slightly different, because each path has taken a slightly different trajectory through the lensing galaxy. If we determine that image A has brightened one day later than image B, for example, this means that the length of the light path producing image A must be one light-day longer than that producing image B. In other words, this delay allows us to measure an absolute distance within the system.
This may not sound spectacular, but it is. Refer back to Figure 2.1 and
consider the geometry of the lensing system. If we know all of the angles
within the system (
,
and
) and we know one distance, then we can deduce all
of the distances including Dl and Ds. If we know
an absolute distance to the lens or source and we know the redshifts, this
is all we need to deduce Hubble's constant.
Everything has a catch however; we need to know the angles.
is easy to measure (assuming we can see the lensing object);
it is just the angular distance
on the sky between the lens and the lensed object. But
and
require us to put in some
information; we need to know the mass distribution of the lens and hence
the degree to which it bends the light.
Doesn't this leave us back where we started? Not quite. We have some constraints on the mass distribution, as described in section 4, and these can be used for our purposes. The problem, however, is that we need the rare coincidence of a lens system with good mass constraints and with a variable background source. Table 3 presents the measurements which have been made so far, with some assessment of how good the constraints are. It can be seen that most of the gravitational lens determinations of the Hubble constant are in the region of 65 kms-1Mpc-1. Most of the determinations, however, have assumed without proof the isothermal ellipsoid model for the lensing galaxy. Relatively small departures from this model can change the Hubble constant substantially - as a rule of thumb, a change in the index of surface mass density of about 0.1 from the isothermal approximation of r-1 causes a change of about 10% in the Hubble constant.
Table 3. Values of the Hubble constant from gravitational lenses. The random errors quoted by the original authors are usually about 10%; however, as we note, the systematic error due to the mass model in many cases may be significantly greater. In all determinations an accurate time delay is needed, but more significant is the ability to constrain the mass model for the lensing galaxy accurately.
| Lens system | H0 value | Authors | Comments |
|---|---|---|---|
| CLASS B0218+357 | 69 | Biggs et al. (Jodrell Bank) | Good prospect; see next section. |
| 0957+561 | 64 | Kundic et al. 1997 | The first gravitational lens, and a very accurate time delay has now been measured due to the large separation of the lens and the consequent long (400-day) time delay. Unfortunately, the large separation comes at a price; it is produced by the fact that the lens consists of a main galaxy together with a large cluster which is fearsomely difficult to model. |
| HE1104-1805 | ? | Wisotzki et al. | This lens was discovered a few years ago and a time delay between its lensed images has been measured. As its name implies, it is a southern hemisphere object. The main problem is that, being only a two-image system, it is difficult to get a well-constrained mass model. |
| PG1115+080 | 42 | Schechter et al. | This is a four-image lens from a radio-quiet quasar. It was one of the first lenses to be discovered, and has been extensively studied because the background object is lensed into arcs, giving good mass model constraints. Unfortunately, there is a large nearby cluster of galaxies whose gravitational effects must be taken into account when constructing the mass model. Depending on the type of model assumed for the lensing galaxy, the Hubble constant determination for this lens was shown by the original authors to vary by 50%, although there are suggestions in the literature that the system can be modelled in such a way as to decrease this. |
| CLASS B1600+434 | 57 | Koopmans et al. | Despite the well-measured time delay, this is still an uncertain determination. This is because, like HE1104-1805, B1600+434 is a two-image lens system and the lens mass model is hard to constrain; moreover, there is a nearby bright galaxy which complicates the mass model further. We have tried hard to detect extended radio structure in both lensed images, which in principle gives extra constraints, but so far without success. |
| CLASS B1608+656 | 59 | Fassnacht et al. | This is a four-image lens, so might be expected to give a good mass model. In addition, time delays have been measured between variations in all four lensed images. Unfortunately, the lensing galaxy is large and complex, and optical images actually reveal two concentrations of light which may be two separate lens galaxies. There is thus no agreed mass model for this lens. |
| PKS1830-211 | 65 | Lovell et al. | This is another very promising lens system. It has extensive radio structure providing abundant constraints on the lens model. As luck would have it, however, it is very close to the line of sight to the centre of our own Galaxy and is therefore difficult to study optically and to determine the lensing galaxy position accurately with respect to the lensed images; a crucial observation. |
A case study: the CLASS lens 0218+357
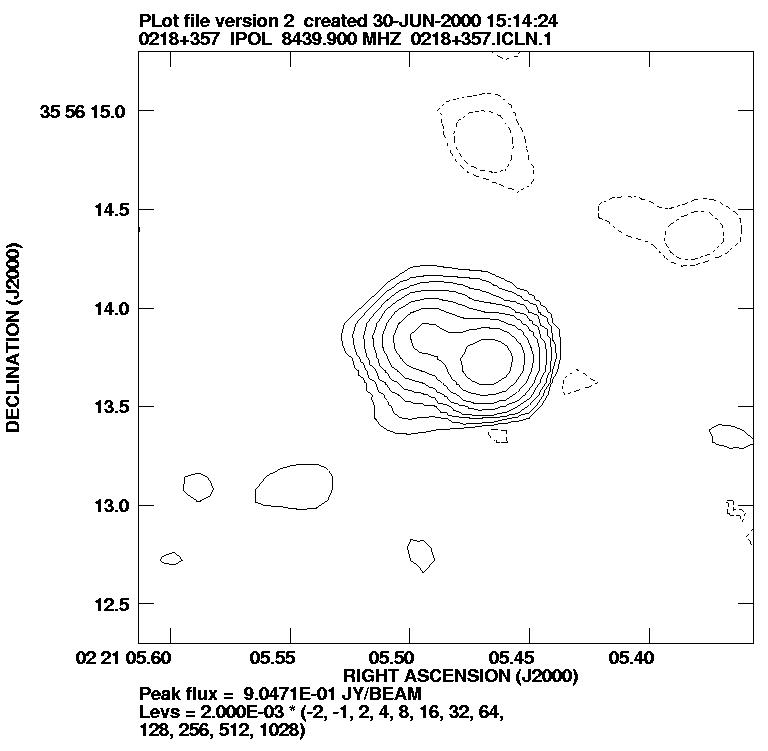
B0218+357 was one of the first lens systems to be discovered in the CLASS gravitational lens survey. Immediate suspicions were aroused by the initial VLA map at a frequency of 8.4GHz (and resolution of 0.22 arcsec), Figure 5.1.
|
|
Figure 5.1. Initial VLA image of the gravitational lens B0218+357 (click to get larger scale view). The double appearance of the central source (note the extension of the contours to the east - left on views of the sky) immediately suggests gravitational lensing, but alternative explanations are still possible. For example, we could be looking at a radio source consisting of a core with ejection of a radio jet. |
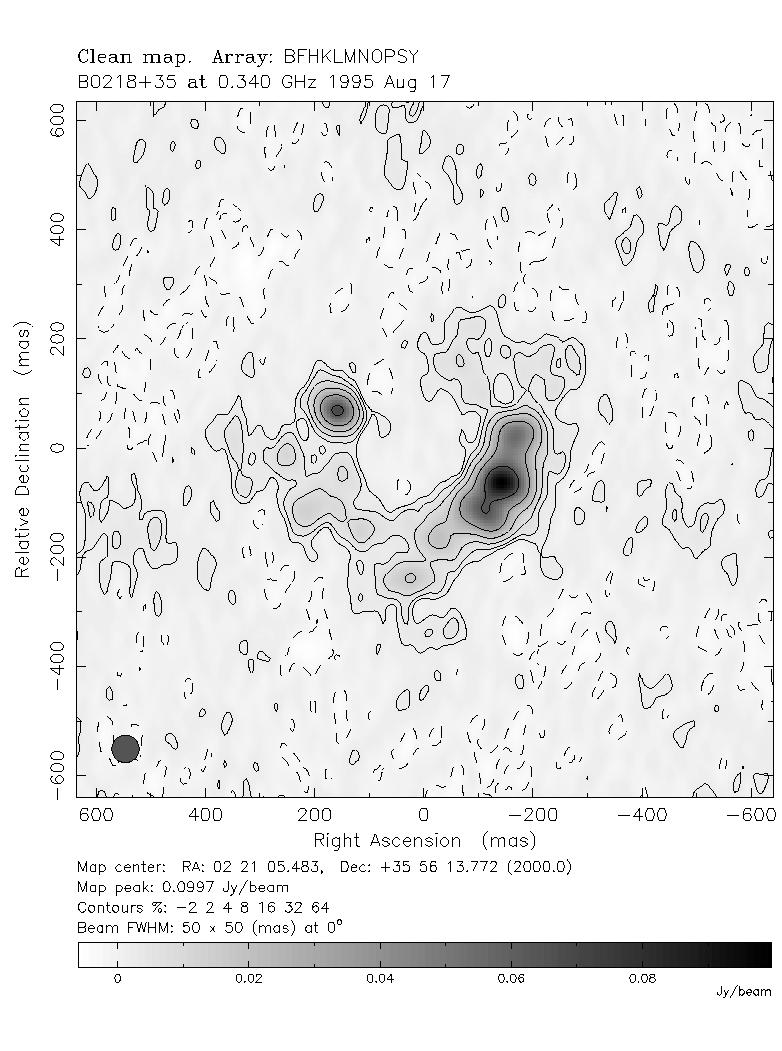
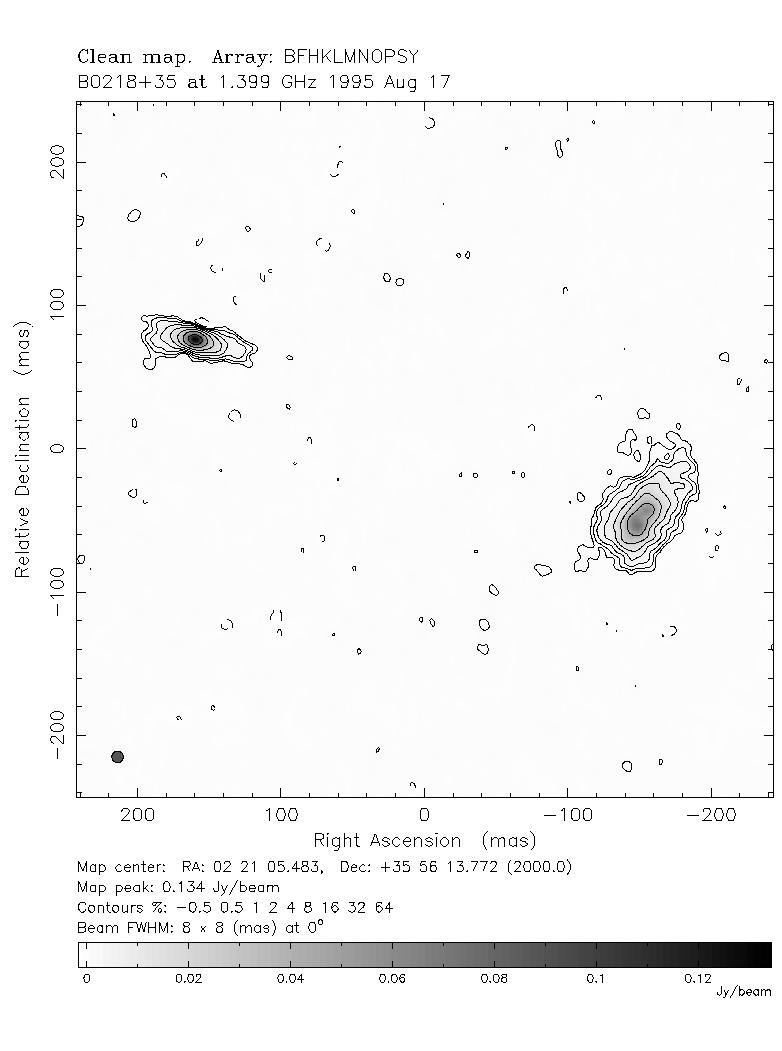
The object was followed up with MERLIN at 0.05-arcsecond resolution and found to be a double-image gravitational lens. Further investigation with the VLBA at still higher resolution showed that both radio components were extended, and that the system contained an Einstein ring, Figure 5.2. The background source consists of a point radio source, which forms the bright double lensed images, and a more extended jet protruding from the source, which occupies a larger area of the diamond caustic and forms the Einstein ring.
|
|
|
Figure 5.2. VLBA radio images of B0218+357 at different frequencies (left: 0.34 GHz; right: 1.4 GHz - note these images show different fields of view; click on the images to get larger scale views). The extended structure in the radio maps can clearly be seen in both images. At lower radio frequencies we see the Einstein ring appearing. | |
| Try to reproduce the configuration of B0218+357 using the gravitational lens simulator with an extended source. |
|
|
Figure 5.3. HST image of the 0218+357 system with a similar field of view to that of Fig. 5.1. The lensing galaxy can be seen as a diffuse circular shape, and the lensed images are the bright blobs. [The bright single pixel at lower left is a cosmic ray]. |
HST images, Figure 5.3, revealed the lensing galaxy in addition to the two lensed images, and spectroscopy gave redshifts of 0.68 and 0.93 for the lens and source. Note that the brighter radio image corresponds to the fainter optical image; the reason for this is not entirely clear but may have to do with dust in the lens blocking one of the light paths.
Further investigation of the lensing galaxy revealed the presence of molecular absorption lines. These are significant because molecular gas is only found in significant quantities in spiral galaxies. The lens galaxy of B0218+357 is therefore almost certainly a spiral. This is supported by the very small scale of the system (at 0.335 arcseconds, one of the smallest lens systems known); spiral galaxies, being less massive, would be expected to cause relatively small splittings.
The background source is a class of active galaxy known as a BL Lac.
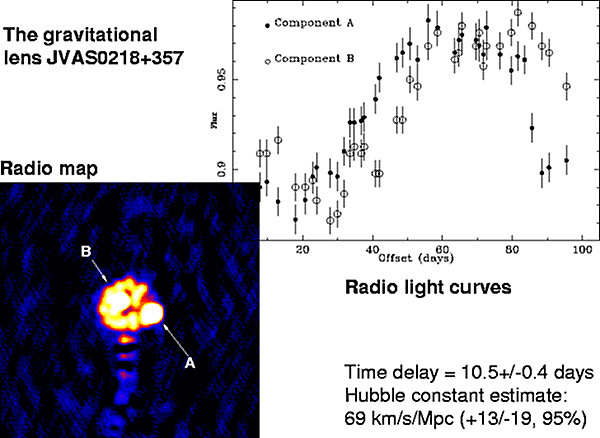
It is highly variable, and a time delay was determined for it by
Biggs et al. in 1999, Figure 5.4. The delay is 10.5 days, and a simple model gives
a Hubble constant of 69 kms-1Mpc-1. The usual
problem rears its head at this point; how confident can we be about the
mass model?
|
|
Figure 5.4. Determination of the Hubble constant using time delays from the gravitational lens CLASS B0218+357 by Biggs et al. The work was carried out by a collaboration based at Jodrell Bank Observatory. Lightcurves are shown for images A and B of this double-image lens from which it can be seen that variations in B lag those in A by about 10 days. Assuming a plausible mass model gives a Hubble constant of 69; work is in progress to refine the mass model and reduce the associated systematic error. |
In this case, a fortunate combination of circumstances means that the mass model can be well-determined. It turns out that the combination of the Einstein ring and the extensive milliarcsecond radio structure provides enough constraints that, in principle, the index of the radial mass profile can be determined to 0.03-0.05 and hence the Hubble constant to an accuracy of 3-5%!
There is only one problem, however. Because of the very small size of the system, it is difficult to find out exactly where the centre of the galaxy is (the galaxy is quite close to one of the optical images and is blended with it). To do the modelling properly and achieve the available accuracy we must know this to within 5 milliarcseconds (approximately every 1 milliarcsecond error introduces an error of just under 1% in the mass model and Hubble constant). At the time of writing, we are awaiting the installation of the new detector system (the Advanced Camera for Surveys) on the Hubble Space Telescope, and have been awarded time to make a very deep observation to try and finally close the loop on this exciting measurement.
In the next section we will look at how gravitational lenses can aid developments in other areas of cosmology.