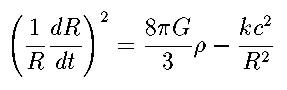
The models described here were first studied by Alexandr Friedman in 1922 and 1924, and independently by Georges Lemaître in 1927. It was not until 1935 that A. G. Walker and H. P. Robertson independently proved that what we now call the Robertson-Walker metric is the only metric consistent with a homogeneous isotropic universe. Universes of this type are therefore variously known as Friedman universes, Friedman-Lemaître universes, Friedman-Robertson-Walker (FRW) universes or Friedman-Lemaître-Robertson-Walker (FLRW) universes.
Here rho is the density of the universe (including the mass equivalent of any energy, according to E = m c ²), G is the Gravitational constant, c is the speed of light as always, and k is the curvature constant that appears in the Robertson-Walker metric.
The term on the left of the Friedman equation is the square of the Hubble parameter:
The Friedman equation can be re-written in a very neat form if we define a critical density
and hence the density parameter
The Friedman equation now looks like:
which shows the importance of the critical density: if the density is greater than this (Omega > 1), the right-hand side is positive, so we must have k = +1 and a closed universe. If Omega =1, we must have k = 0, and for smaller densities the universe is open (in the simplest topology). If k = 0, this last form reduces to the unhelpful 0 = 0. This is because in this case the scale factor R is not determined absolutely; instead one can choose it arbitrarily at some reference moment and the Friedman equation then determines how it changes with time.
The key to solving the equation is to find how the density (or equivalently Omega) depend on R. Imagine a box with co-moving observers at its corners: the amount of matter in the box stays the same as the universe expands, because the universe is homogeneous; all regions behave in the same way so, for instance, no region can have a net gain of matter with respect to its surrounding regions; any random motion of atoms (or galaxies) should cancel out on average. The volume of the box scales as R ³, so we expect the matter density to behave as:
The energy density of radiation falls more quickly than this, because although the number of photons is preserved, each photon expands with the universe and hence loses energy because its frequency is falling. Running the universe back in time, the radiation energy density increases faster than the matter density and eventually overtakes it. However, this happens so close to the beginning of time (when R was about a thousandth of its present value) that we can ignore this short period and leave radiation out of the calculations.
But there is yet another component that we should worry about, the cosmological constant. This was put into GR by Einstein (although he later regretted it). It corresponds to an effective density that is independent of R, and might even be negative! As the matter density in the universe falls, the cosmological constant becomes more and more important, and eventually dominates. A positive cosmological constant corresponds to an effective negative pressure, equal and opposite to its energy density. Work done by expansion agains this "tension" creates the extra energy that allows the energy density to be constant when the volume of each bit of the universe is increasing. In GR the true source of gravity is not just mass (or density, for spread-out stuff) but:
Here the symbol Lambda, as is conventional, denotes the density corresponding to the cosmological constant: the important thing is that negative pressure counterbalances gravitational attraction - just the opposite of what you might think!
The Friedman equation is just a first-order differential equation and can be integrated (numerically, except for the simplest cases) to give the history of the universe in the form t(R). This function is fixed by just two parameters which can take a continuous range of values, and the curvature constant k= -1, 0, or +1. For the continuous parameters we could choose
Conventionally we use the density parameters at the present time:
This choice has the nice feature that we don't have to worry about k explicitly, as it given by the sign of Omega-1. On the other hand, there is a drawback: there is nothing special about the present time, so we are inserting an extra scale (the Hubble time tH = 1 / H0 , i.e. the inverse of the present-day Hubble parameter) into the equations, which complicates matters a bit. Notice that because H changes with time, so does the critical density, and so the density parameters (Omegas) change with time in a moderately complicated way.
You can click in the left panel to choose a model universe; the corresponding R(t) curve will be plotted at right. Notice that the axes in the right panel are scaled by tH and the present size of the universe: for absolute (dimensional) scaling we need to specify H0 as well.
As noted above, the Omegas change with time. Therefore as a given model universe evolves, its position in the left-hand graph changes, sweeping out a particular curve. If you check the box "Plot Omega(m)-Omega(Lambda) trajectories", this curve is also displayed. Check the "Enable Animation" box to plot both curves slowly enough to see how the two are related. Choose "Plot All" instead of "Plot latest" to see all the curves you have generated so far (this gets a bit complicated after a while; you can clear the models one by one or all at once with the buttons).
As the two Omegas fix the evolution of the universe (apart from overall scaling), there is only one curve in the left-hand plot leading to and away from each point, i.e. the curves do not cross. Along each curve, the solutions to the Friedman equation differ only in the sense that the "present time" corresponds to different stages in the evolution of the universe. If we ignore such parochial issues, we really only need one continuous parameter to describe all the universes (apart from overall scale); or rather, several different one-parameter families are needed to cover all possibilities.
Clicking on the graph shows that (nearly) all universes start at the Einstein-de Sitter point with Omega(m) = 1 and Omega(Lambda)=0. This is because if there is a Big Bang (R goes to zero) the density, hence H, hence the critical density, all tend to infinity at R = 0. So Omega(Lambda) tends to zero, while the matter density tends to the critical density. Technically, there are solutions with zero matter density which start at the Milne point where both Omegas are zero; however these obviously do not describe our universe!
The coloured lines divide the plane into six regions, in each of which the universe has a rather different character.
The blue line represents a density parameter of 1, i.e. k = 0. Above this line, universes are have positive curvature and must be closed, below it they have negative curvature and can be open. As we saw above, universes cannot change from spherical to hyperbolic geometry, so the evolution tracks never cross the blue line.
The line Omega(Lambda) = 0 separates universes with negative and positive cosmological constant. Negative values mean that the universe always recollapse eventually: the expansion halts and reverses at a certain point. Since at turnaround H = 0 by definition, the critical density at turnaround is zero, so the evolution tracks of universes with turnaround extend out to infinite density parameters on both axes. After turnaround the collapse is a time-reversed version of the expansion (note that the Friedman equation specifies only H ² and so doesn't fix the sign of expansion/collapse). These "Bang-crunch" universes with Omega(Lambda) < 0 form our first family of solutions.
The second family are the positive cosmological constant models bounded by the green and red lines. These represent universes which expand continuously from R = 0 to infinity. They start from the Einstein-de Sitter point and end at the de Sitter point, i.e a universe with zero matter density and critical density in the cosmological constant. This is because a positive cosmological constant will eventually dominate the total density as it does not fall at all as the universe expands. All of these tracks could be traversed in the opposite direction, i.e. with a continuous collapse from an initially-infinite de Sitter universe to an Einstein-de Sitter big crunch. Obviously these collapse models don't correspond to our Universe.
The limiting case for an expanding, positively curved universe is the loitering universe, which is shown by the curved green and red lines. Loitering universes reach a point with H = 0 and also zero acceleration, known as an Einstein solution (which lies at infinity on this graph because the critical density is zero). Along the green line the Einstein point is in the future, while it is in the past along the red line. At the Einstein point the repulsive negative pressure from the cosmological constant exactly balances the gravitational attraction of density:
This is a delicate and unstable balance. If the density is slightly too high, the universe will collapse from the Einstein point, following the green line down to a big crunch at the Einstein-de Sitter point. If the density is too low, the expansion takes off and the universe follows the red line to the de Sitter point of total domination by the Cosmological constant.
The third family of Friedman solutions are the ones with positive cosmological constant, but which fall to the left of the green loitering line. For these, the repulsive term is not enough to prevent recollapse, so they expand from the Einstein-de Sitter point to a turnaround at infinity, and then recollapse back to a big crunch along the same track. This family is effectively continuous with the first family (negative cosmological constant) through the case with Lambda = 0. Thus all the tracks to the left of the green line expand from a big bang and recollapse to a big crunch.
The fourth family are those to the right of the red loitering line. In these universes the cosmological constant is so large that, projecting the universe back in time, the expansion turns around in the past; these are the bounce models, in which the universe collapses from infinity (contracting from the de Sitter point), bounces (both Omegas are infinite at the bounce as H = 0 here just as at turnaround in "bang-crunch" universes), and then re-expands, finishing in an expanding de Sitter phase. Note that the limiting case here is when the universe collapses from infinity to bounce at exactly the condition for an Einstein universe, thereby following the red curve away from the de Sitter point. The third and fourth families of solutions mathematically form two branches of the same solution of the Friedmann equation.
Bounce and (past) loitering universes are ruled out observationally: they predict a maximum redshift corresponding to light emitted at the bounce, or a pile-up of galaxies with redshifts corresponding to the loiter point. The highest observed redshift is 6.68, which implies that the universe has expanded by a factor of Z = (1 + z) = 7.68 since then. But to get a bounce or loiter that far in the past, we would have to be well into the de Sitter phase by now, i.e. very close to the de Sitter point on the graph: specifically, for the bounce to be at z = 6, we would need Omega(matter) < 0.006, whereas observations show that it is certainly greater than 0.1, probably greater than about 0.3.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .