The Robertson-Walker Metric

The simplest universe consistent with SR is one which appears isotropic (the same in all directions) to a set of privileged observers, called co-moving observers because each observer sees the others as moving along with the overall cosmic expansion. (Actually these observers are just a figure of speech - the important thing is that there are sites from which the universe would appear isotropic if there were anyone there to observe).

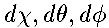
The existence of three or more such observers places very strong constraints on the possible structure of space-time. For a start, there is a "natural" time coordinate: the time as measured by each co-moving observer, equipped with a standard clock. Notice that their clocks all measure the same time because they are all controlled by the same rules of physics, and the observers can synchronize their clocks by agreeing to define t=0 to be some special moment in the life of the universe, for instance its beginning (if it had one). The existence of a cosmic time is an enormous simplification; without it, there is no sensible way of separating space from time in the 4-D continuum of space-time. Next one can show that in such a universe there could be a co-moving observer at every point, all of whom see the universe as isotropic, i.e. 3 co-moving observers imply an infinite number of co-moving observers.1 Next, you can show that at a given time, the universe is homogeneous (the same at all points). Finally, there is also a "natural" way of fixing space coordinates: we can choose co-moving co-ordinates which move along with the co-moving observers (this gives us a way of defining what we mean by the "same" point at different times).

In such a universe, the interval (space-time separation) between events ("points" in space-time) can be described by the Robertson-Walker metric. By fixing the distances between all points, the metric also defines the geometry of space-time, and, because there is a meaningful cosmic time, the geometry of space at a given time. In fact, there are only three possibilities for the local geometry of space, because the curvature of space must be the same at all points (homogeneity) and not pick out any particular direction (isotropy):

Positive Curvature
The sum of the three angles of a triangle is more than 180°, (although this is only noticable for triangles with sides comperable to the radius of curvature, R). This case is denoted by setting the curvature constant k to +1. A 3-D space with positive curvature has a structure analogous to the 2-D surface of a sphere: if you travel far enough in any direction, you come back to where you started. Thus space is finite and the universe is said to be closed.
Flat space
The conventional geometry of Euclid. k = 0. This can be considered as the limit of the other two cases for infinite radius of curvature. Because it is balanced between the other two, this is sometimes called a critical universe.  For true Euclidean geometry, the topology is also open, meaning that space is infinite in all directions. It is also possible to have compact topologies (e.g. the 3-torus) in a flat space, which
have finite volume (and so are closed).
Negative Curvature
The sum of angles of a triangle is < 180°, (again, noticable only for very large triangles). k = -1. This is the hardest case to imagine as it is not even possible to have a 2-D surface of constant negative curvature (a pseudosphere) in Euclidean 3-D space. 2-D surfaces can have local regions of negative curvature, e.g. saddles and trumpet cones. The simplest topological case is when the universe is infinite in all directions, and so said to be open. In fact it is "more infinite" than the Euclidean case, in the sense that at a given distance from us there is more space than we would expect from Euclidean geometry.  As for flat space, there are compact topologies with negative curvature, which are closed.
Note that the metric is unaffected by topology, which simply restricts the possible values of the coordinates. The RW metric is encapsulated in the equation for the small interval ds between events separated by time dt and co-moving space-coordinates
dchi, dtheta, dphi
which is:
ds˛ = (c dt)˛ - R˛(t) [ d chi˛ + S ˛_k(chi) ( d theta˛ + sin˛ theta d phi ˛ ) ]
In this equation the evolution of the Universe is governed by the scale-factor R(t): the term in square brackets is the square of the co-moving distance, dl ², and the physical distance between two points is just R dl. At the moment R is increasing with time, which is another way of saying that the Universe is expanding.

The geometry of space at a given time is defined by the function Sk(chi), which is just a neat way of writing the 3 different functions needed for the 3 values of k:
k Sk(chi) Curvature
+1  sin(chi) Positive
0  chi zero
-1  sinh(chi) Negative

Notice that the geometry of space cannot change with time in a homogeneous universe: if the curvature is negative to start with, it stays that way. The same applies to topology: a fundamental observer's neighbours cannot suddenly (or gradually) change with time.

Back to the Friedman Equation Back to main Cosmology page

1 This does not mean the universe seems isotropic to every possible observer. Although SR emphasises that all observers should be treated equally, in cosmology the co-moving observers are more equal than others: anyone who presumes to move relative to them will get a distorted view of the universe in which the observer's direction of motion relative to the co-movers will pick out a special direction in space. 

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.