PHYS20171 MATHEMATICS OF WAVES AND FIELDS

Web Resources

An extremely useful resource is the HELM project which is available from the School of Mathematics. (Follow the HELM link in the menu on the left. You will need to login using your university username and password to access HELM.) It provides a set of workbooks covering a wide range of mathematical topics. The most relevant for this module are Sections 23, 24 and 25. Note that in some areas these workbooks provide more detail than is covered in this module, whereas in others this module goes into greater depth.

Fourier Series

• Fourier series applet

Fourier Transforms and Convolution

• Fourier transform applet from Nicolas Schoeni and Gervais Chapuis Ecole Polytechnique FC)dC)rale de Lausanne, Switzerland.
• Fourier transform tool. Click the button on the page to launch the applet.
• Nice discussion of convolution from Wolfram MathWorld. Source of animations shown in lecture.
• Java Applet to demonstrate convolution with discrete functions
• Java Applet to demonstrate convolution with continuous functions
• Wikipedia entry on convolution. Some nice animated graphics graphically showing convolution.

Waves

• Group velocity applet showing a wave packet and the effect of changing the group velocity
• Some figures and notes about waves
• Wikipedia pages discussing:
  • wave packets
  • group velocity
  • phase velocity

Applets and movies

Many of these links are taken directly from Mike Birse's course page.

• Video of vibrations on a circular membrane (drum head).


• Video showing salt being used to trace the nodal lines on a square vibrating plate.


• Video showing salt being used to trace the nodal lines on a circular vibrating plate.


• Fourier synthesis (with sound) by Tom Huber (Gustavus Adolphus College, Minnesota)


• Fourier synthesis (with sound) by Fu-Kwun Hwang (National Taiwan Normal University), via a mirror site at Aberdeen


• Vibrating string by Paul Falstad


• Vibrating bar and other one-dimensional waves by Paul Falstad. A more general version of the preceding applet. Try the string setup with different boundary conditions (pinned/free and free/free).


• Rectangular membrane by Paul Falstad


• Circular membrane by Paul Falstad


• Rectangular membrane movies by Dan Russell (Kettering University, Michigan)


• Circular membrane movies by Dan Russell (Kettering University, Michigan)

Spherical Harmonics

• Figure showing the real spherical harmonics Y_l,m for l=0 to 4 (top to bottom) and m=0 to 4 (left to right). The negative order harmonics Y_l,-m are rotated about the z axis by 90^o/m.
• Schematic representation of Y_{\ell m} on the unit sphere and its nodal lines. Y_{\ell m} is equal to 0 along m great circles passing through the poles, and along \ell-m circles of equal latitude. The function changes sign each time it crosses one of these lines.
• 3D color plot of the spherical harmonics of degree n = 5
• A java applet which displays the wave functions of the rigid rotor (rigid rotator), which are the spherical harmonics.
• Wikipedia entry (source of the figures above)
Video showing the 3D standing waves in a sphere
• Video waves in a sphere of water. An experiment from the International Space Station.

Figures, Images and Diagrams Used in Lecture

• Convolutions
  • Animated convolution 1 (Image from Wikipedia, see link above.)
  • Animated convolution 2 (Image from Wikipedia, see link above.)

Examples of applications

• An image of the temperature fluctuations in the cosmic microwave background from the WMAP mission after 5 years of observations.

  

  This image has been decomposed using spherical harmonics to produce a power spectrum to show the temperature fluctuations as a function of angular size scale. The image below shows this decomposition. The points are the measured values and the curve the predictions of a model.

  

  (These images are from the WMAP website.)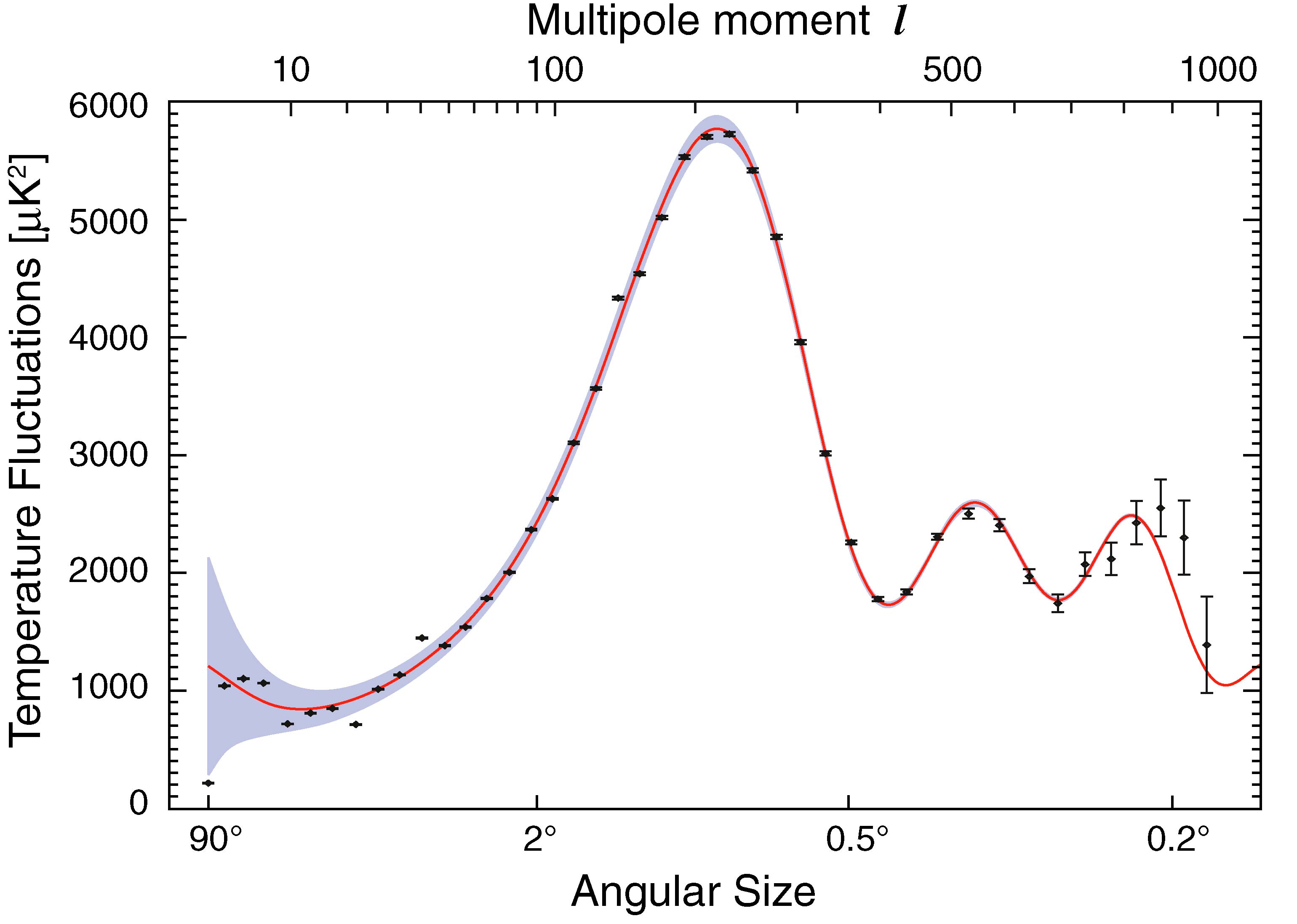
• The science of cooking:
  • Heston Blumenthal
  • Molecular gastronomy
  • A book about science in the kitchen