6. Searching for Pulsars
Given the large variety of pulsar applications, it is obvious that finding new pulsars still promises to be very rewarding. Obviously, with a larger sample of pulsars, we can infer more reliably what the population of pulsars in the Galaxy might be and better determine its mean parameters like birth rate and spin period. Moreover, the chances of finding pulsars that will improve our knowledge in different areas of physics, e.g. by finding exotic systems or pulsars which enlarge our parameter space, increases with the total number of pulsars discovered. For instance, it has been estimated that there should be one pulsar-black hole system in every 1000 pulsars discovered. Given that by the time of writing (Nov 2003) about 1700 pulsars were known, there is an increasing prospect that such an exciting system can be found soon. However, in order to detect such a system, the survey parameters have to be chosen carefully and certain techniques must be applied.
6.1 Search parameters
When designing a search for pulsars a few parameters have to be chosen depending on the specific aim of the survey. First, we have to decide whether we would like to find young pulsars, or millisecond pulsars, whether we want to study globular clusters, the inner Galaxy or even the Magellanic Clouds, or whether we want to establish as whether an unidentified X-ray or radio source is in fact a pulsar. Depending on the choices the search parameters are determined.
Pulsars are born in the
Galactic plane and this is the reason why, as illustrated by Figure 1,
we find the majority of pulsars
close to these locations.
|
|
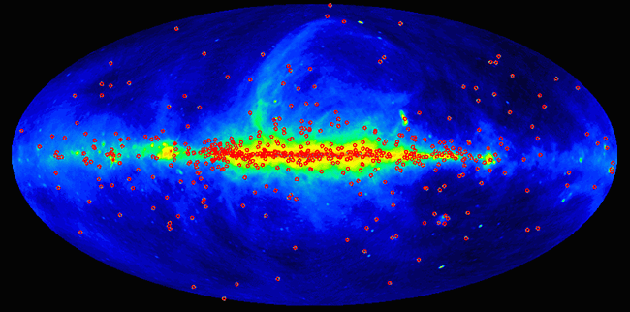
Figure 1. The radio sky as seen in the famous 408-MHz survey with known pulsars superimposed as red circles. The Galactic plane is easily visible as the bright horizontal band. |
Many pulsars seen in Figure 1 to be well above or below the plane are actually nearby pulsars and only appear to be at such high galactic latitudes while they are in fact still close to the plane. However, as we have mentioned before, pulsars exhibit very high velocities, and therefore it is actually possible for some pulsars to travel large distances away from the plane during their lifetime. Therefore, if one wants to discover predominantly young pulsars, for instance to study birth periods, associations with supernova remnants etc, one should search along the Galactic plane when the pulsars are still close to their birthplace.
The sky area to be searched is therefore the first parameter to be decided. If you want to find, for instance, millisecond pulsars, then a good strategy is obviously to look at globular clusters which have old stellar populations. The example of 47 Tucanae described before shows how successful one can be. Searching areas away from the Galactic plane obviously must typically result in the discovery of older pulsars too, as it takes some time for the pulsars to reach this position.
At best, of course, one should search the whole sky. However, that needs usually at least two telescopes (for the Northern and Southern sky) and it obviously needs a long time to complete such survey. As we have seen, the sensitivity increases with the square-root of the integration time. Hence, for an all sky survey, one can only afford to observe for a short time at a given position in the sky, rather than spending hours which may be possible when searching only a small area. The integration time is therefore the second parameter to be decided, as it will - together with the size and sensitivity of the telescope to be used - determine the sensitivity of the search. For targeted searches, one knows exactly the position to search for a pulsar, as it may be a small globular cluster or given by an unidentified continuum source or, for instance, by the position of a X-ray or gamma-ray point source. In these cases, only one pointing or so has to be made, and a long integration time can possibly be afforded to reach very low brightness limits.
The next important search
parameter is the radio frequency at which the search should be performed.
As we have seen in Part 2, pulsars are brightest at around
a few hundred MHz, while the intensity decreases quite rapidly towards
higher frequencies. Obviously, the first choice would be a frequency at
a few hundred MHz. However, we have also seen in Part 3, that the pulses
suffer from the propagation effect of dispersion. The dispersion effect,
largest at low frequencies, smears the pulses and makes them more difficult
to detect. Using filterbanks, we can account for dispersion, but there
is another yet to be mentioned propagation effect, which cannot be removed
by any instrumental technique and hence may be more important.
|
|
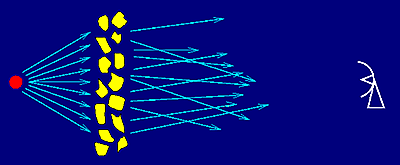
Figure 2. Illustration of scattering of rays from the pulsar as they pass through a clumpy interstellar medium. |
The electron distribution causing dispersion is not homogeneous throughout the interstellar medium, but it shows a certain "clumpiness". As illustrated in Figure 2, the clumps are large enough to scatter the radio waves into different paths.
Due to scattering, some
rays can now make their way to the telescope which would otherwise have
missed it. These rays, however, have a longer path length and will therefore
be slightly delayed compared to those signals which travel straight.The
pulses become smeared again, showing an exponentially decaying tail and
are therefore again more difficult to detect than without scattering. Scattering
is heavily reduced at higher frequencies, e.g. it is a factor of 250 less
severe at 1400 MHz than it is at 400 MHz, see Figure 3.
|
|
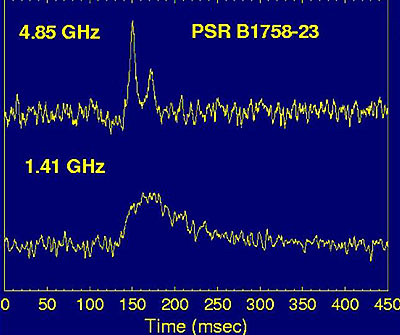
Figure 3. In this example a pulse at 1400 MHz is severely scattered, lower panel, but shows no sign of scattering at 4850 MHz where we can finally observe the true pulse shape. |
Scattering is strongest in those regions where we expect the largest densities of electrons, i.e. the Galactic plane and in particular the regions towards the Galactic Centre. Since scattering cannot be removed by any other means than observing at higher frequencies, a survey of the Galactic plane or the inner Galaxy in general, should be done at a frequency of at least 1400 MHz. This also reduces the effect of dispersion, and a smaller number of filterbank channels is needed to cover a large bandwidth, which in turn should be maximized to obtain best sensitivity.
Naturally, the choice of search parameters is usually a compromise in one way or another. In summary, we have to decide on:
- sky coverage,
- frequency,
- bandwidth,
- number of filterbank channels,
- integration time,
- sampling time.
The last item, the sampling time, will be discussed in more detail when we review the search techniques in the next section. It is important as it determines the fastest period pulsar that we are able to find. However, a short sampling time, together with the number of filterbank channels, increases the data rate and we have to ensure that this we can handle this both in rate (bytes per second) and volume acquired during the whole survey. Issues like number of bits used to digitize the data are related but will not be discussed here.
6.2 Search techniques
Even if the pulsar signal is usually weaker than the thermal noise of the radio receiver or other background signals, pulsars can be still detected due to the regularity of their beacons, providing that the integration time is long enough. A technique looking for periodic signals in regularly sampled data is called a (discrete) Fourier transform. Computing the Fourier transform of the incoming data measured as a function of time means to derive a power spectrum, which reveals the amount of power in the original time series for a range of frequencies. In the presence of a periodic signal, such as a sine wave, a spike will occur in the power spectrum at the frequency of the periodic signal. This signal is called the "fundamental". If, as is the case for pulsars, the signal is periodic but not a sine wave, a number of additional spikes at integer multiples (i.e. 2x, 3x, 4x etc) of the fundamental period occur. These are the "harmonics" and their number increases with decreasing pulse width.
During the search process,
the Fourier spectrum is computed by applying an algorithm called the Fast Fourier
Transform (FFT) and the result is then searched for fundamentals and their
harmonics. Before this can be done, however, we have to correct for the
effects of dispersion by delaying the signals of the high freqeuncy filterbank
channel, which had been recorded independently. But since the dispersion
measure is of course unknown prior to the discovery, we have to assume
a number of trial values. Therefore, the data are de-dispersed for a wide
range of possible dispersion measures, and each resulting time series is
then subject to the Fourier analysis. The best candidates are
recorded with the derived period and dispersion measure and later re-observed
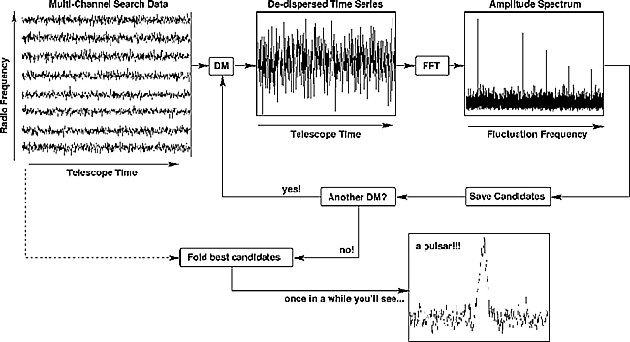
at the telescope. The process is summarized in the Figure 4.
|
|
Figure 4. Flow diagram of the pulsar observing process: (1) data are obtained as a function of time in a number of channels of different frequencies; (2) given a value for DM the data are dedispersed; (3) the Fourier power spectrum reveals candidate frequencies for the pulsar (plus harmonics); (4) the parameter values for the candidates are saved; (5) another DM is chosen and the process 2-4 repeated; (6) when the full range of DM required has been searched the original time series data can be folded on the periods suggested by the Fourier analysis perhaps revealing a pulse. |
The range of frequencies, and hence pulse periods, which can be searched is determined by how fast we sample the data received from the telescope. Sampling in time intervals of length ts, the maximum frequency which can be investigated is given by the "Nyquist frequency":
As one usually only believes pulsar candidates which are sampled with at least a few measured time intervals across the pulse period, one is effectively only sensitive to periods of 2 or 4 times the theoretical limits. However, most modern searches use sampling times of around 50 to 250 microseconds, resulting in Nyquist limits of 100 to 500 microseconds. Hence, such searches should be able to discover pulsars with sub-millisecond periods if they exist.
6.3 The Parkes Multibeam Pulsar Survey
|
|
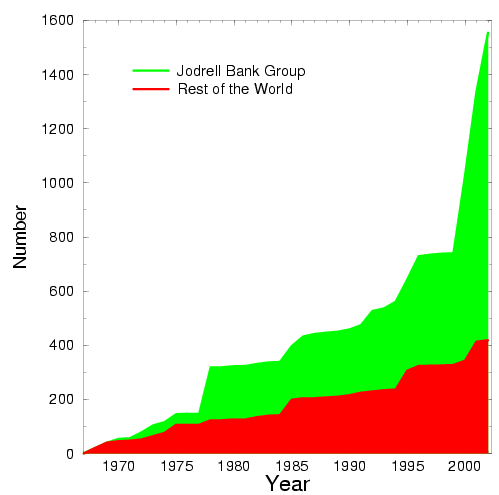
Figure 5. Number of known pulsars as a function of time since their original discovery. Note the sudden increase in the discovery rate due to the Parkes Multibeam Survey starting in 1997. |
The techniques described above are successfully applied in the recent Parkes Multibeam Survey which, by its completion, will have discovered as many pulsars as all previous surveys put together, see Figure 5.
This survey is designed to find young pulsars and is therefore concentrating on the Galactic plane.
In order to reduce scattering and dispersion effects, a frequency
of 1400 MHz is used. The key to the success of this survey lies in its unprecedented
sensitivity, which is achieved by a unusually long integration time of 35
min per pointing. This is only possible since a multi-beam receiver, shown in Figure 6, is
used which covers 13 different positions on the sky at once, so that despite
the long integration time the whole search area can still be covered efficiently.

|

|
|
Figure 6. At left, the Parkes Telescope in Australia. At right, the 13-beam receiver being hoisted to its position at the focus of the Parkes Telescope. |
|
|
|
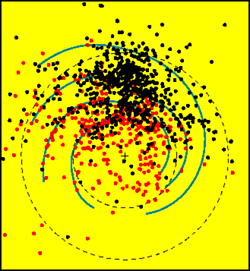
Figure 7. The positions of the known pulsars in the galactic plane before (black) and after the Parkes Multibeam Survey (red). Positions of spiral arms are indicated by blue lines and the galactic centre by a cross. |
The survey has not only already discovered a large number of interesting, exciting systems (e.g. a pulsar with the most massive companion of at least 11 solar masses, or radio pulsars with the highest surface magnetic fields known) but will also provide an extremely useful way of studying the pulsar population and the properties and structure of the Milky Way. This becomes obvious upon, for example, examination of the effect of the survey on the distribution of known pulsars shown in Figure 7.
6.4 Acceleration searches
The Fourier
analysis described above is only efficient if the period of the signal to be detected remains
constant during the integration time. If the period is changing, for instance
due to binary motion of the pulsar and the resulting Doppler effect, the
amplitude of the signal in the computed spectrum will be spread out and more
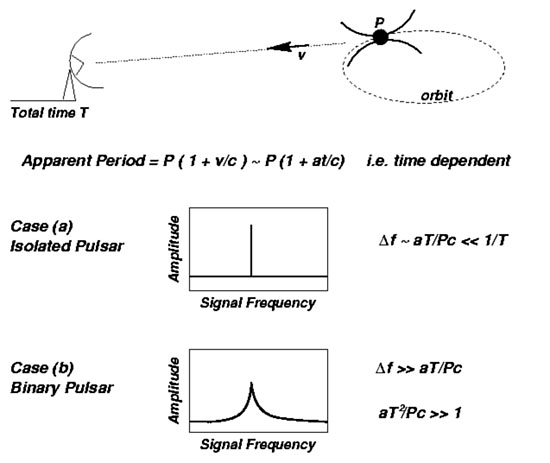
difficult or even impossible to detect, see Figure 8.
|
|
Figure 8. Loss of search sensitivity to short-period binary pulsars due to smearing of the signal in the power spectrum. |
Therefore, as Figures 8 and 9 illustrate, it is difficult
to discover pulsars in short binary orbits, where the integration time
is of similar size as the orbital period. Such systems can only be discovered,
if the pulsar is either very strong or special techniques are applied to
account for these effects. Such acceleration searches do not only search
for periods with various trial dispersion measures, but they also assume certain
accelerations of the pulsar due to a variety of orbits. A number of such
techniques are currently developed and applied. One approach is to assume
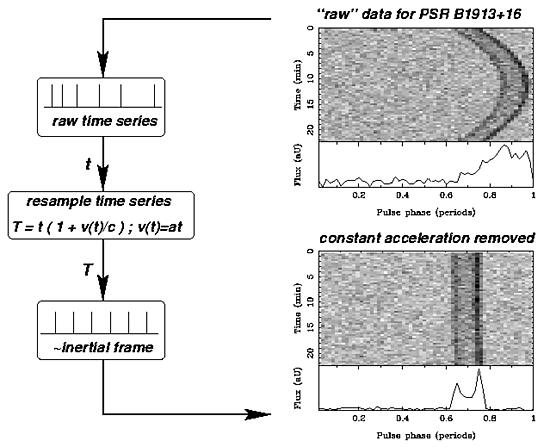
that any acceleration is constant, and the measured time series is
strechted or squeezed in time to correct for that, Figure 9. This corresponds to
a transform of the measured time series into an inertial frame of reference
where the pulsar is at rest.
|
|
Figure 9. Illustration of an acceleration search aimed at improving the signal to noise in a binary pulsar search. |
This and other acceleration search techniques are computationally very expensive and it still needs large computational power to perform these searches. At Jodrell Bank we have been using a supercomputer at the University of Manchester to carry out acceleration searches and, in the near future, will be moving over to our own specially-designed COBRA supercluster. However, recent success shows that such approaches are working and rewarding.
