7. Other types of lensing

Microlensing

Principles

So far we have considered lensing by whole galaxies, of a typical mass of around 10¹¹ solar masses. There is of course no reason why individual stars cannot act as gravitational lenses (it was after all observation of deflection of light by the Sun which was the first confirmation of the basic principle).

However, the Einstein radius of a star (the diameter of an Einstein ring produced when the star lenses a background object) is very small - typically less than a milliarcsecond. Splittings on this scale are undetectable with current optical instruments. But gravitational lensing also magnifies the background image, and this effect is observable.

1. Use results in the previous exercises to calculate the Einstein radius, in arcseconds, produced when a star at a distance of 10 kpc lies exactly behind a star of 1 solar mass (2x10³⁰kg) at a distance of 5kpc.

Suppose we have a gravitational lens which moves in front of a background object (Figure 7.1). As the lens moves across, the background source will appear to brighten as the lens moves closer, and will fade again when the lens moves away again. This will lead to a characteristic change in brightness with time in the background object known as microlensing.

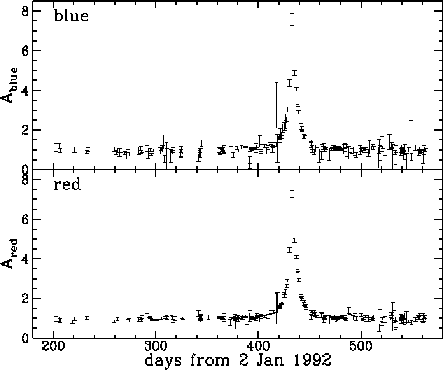
Figure 7.1. This figure is taken from the webpage of the MACHO project, and shows a microlensing event. Note the sudden brightening and fading of the star as the lensing object passes across it. The pattern is similar in the red and the blue, indicating that the effect is indeed due to lensing rather than an unusual variation intrinsic to the star (which would be expected to be colour dependent).

Searches for microlensing

Because the Einstein radius of a star at a typical distance of a few tens of parsecs is very much smaller than a galaxy at a few Megaparsecs, lensing by stars is very much more difficult to spot. The chances of success with any given star are very small - something like 1 per million stars rather than 1 per 500 as in the case of quasars being lensed by galaxies.

As is often the case in astronomy, advances in technology came to the rescue in the early 1990's. The particular breakthrough was the ability to manufacture very large CCDs for optical telescopes, which allowed one to cover a very large field (about one square degree or more). If such a system is used to look at a very dense star-field - towards the centre of our own Galaxy, or towards the centre of a satellite galaxy known as the Large Magellanic Cloud (LMC) - the required number of stars can be observed in only a single night's observing. The requirement is then to monitor these stars over a number of nights. What is being looked for is an event where a foreground object passes directly across the line of sight to an LMC or Galactic star in the background field. In this case there will be brightening, due to the magnification effect of gravitational lensing, followed by a fade as the foreground object moves away, as has already been seen in Figure 7.1.

Several collaborations have been set up to look for these effects, and the most successful have been the MACHO (Massive Compact Halo Objects) programme, and OGLE (Optical Gravitational Lensing Experiment). Hundreds of such events are now known.

Microlensing results

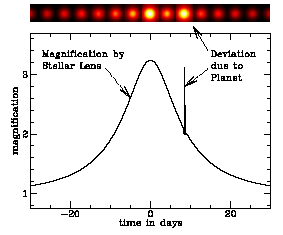
Figure 7.2. This figure is taken from the webpage of the Microlensing Planet Search, and shows a spike in a simulated microlensing event due to a planet orbiting the lensing star.

Microlensing has a unique place in searches for dark matter on scales of order 1 solar mass. The results so far from collaborations such as MACHO which explore the line of sight through the halo of our galaxy towards the Large Magellanic Cloud indicate that dark objects are being found in the halo of our own galaxy and/or the halo of the Large Magellanic cloud, with typical masses of a few tenths of a solar mass. The halo of our Galaxy cannot be entirely composed of such objects, but about 20% is a likely figure. Other experiments which look through our galaxy along the line of sight to the Galactic bulge find a rather larger number of lensing events than expected. Whether these are due to roughly solar-mass stars or brown-dwarf "failed stars" is still an open question.

Another important microlensing research area is the search for binary lens systems and lens systems containing planets. A binary lens system will produce a more complicated magnification pattern, resulting in a more complicated variation in brightness of a background object as the binary lens passes it. If the lens contains a planet, the brightness variation of the background source will show an essentially normal profile, except for a very brief spike due to the planet, see Figure 7.2. Unlike extrasolar-planet search techniques such as spectral detection of the induced wobble of the parent star, the gravitational microlensing technique is capable of detecting planets down to Earth mass. Active research in this area, including a handful of planet detections, is conducted by the Microlensing Planet Search which monitors microlensing events intensively upon notification by larger searches such as MACHO and OGLE. It is also worth looking at the MOA web pages – they recently reported discovery of a planet.

Lensing on large scales

As well as lensing on very small scales, by individual stars within our Galaxy, we can see lensing on much larger scales, which is done by whole clusters (i.e. large groups) of galaxies. The nearest cluster of galaxies is the Virgo Cluster, at a distance of about 20 Mpc, but other much bigger clusters are known. The most massive clusters can have mass of 100-1000 times that of our own Galaxy.

The centres of clusters can produce multiple images of very distant galaxies which lie behind the cluster. However, the most spectacular effect is that of gravitational arcs, which arise due to the distortion effect of gravitational lensing. Figure 7.3 shows one of the many spectacular pictures which have been taken of this effect. The detailed structure of the images can be used to infer the mass structure of clusters and recover important cosmological information.

Figure 7.3.The cluster of galaxies Abell 2218 in a picture taken by the Hubble Space Telescope (click for larger scale view). The large galaxy to the left of centre lies at the centre of the cluster. The stretched arcs towards the outer edge are not galaxies within the cluster, but background galaxies immensely stretched and magnified by the gravitational field of the cluster.

In the next section we will look at prospects for the future in studies of gravitational lensing.

Answers to questions

Answer to question

The radius is 0.0009 arcseconds.

For this we need the point-source Einstein radius formula derived earlier: ²=4GMD_ls / c²D_lD_s. Using D_ls=D_l=5kpc and D_s=10kpc, remembering to convert to metres, gives =4.4x10^-9 radians, or 0.0009 arcseconds.