6. Cosmology

Principles

Gravitational lensing is an excellent astrophysical tool because it is sensitive to any sort of mass, independent of light emission. Much of modern cosmology concerns the amount and nature of mass in the Universe, and gravitational lensing is therefore very important. In principle, searches for gravitational lenses can tell us about stellar densities in galaxy halos, compact dark masses, and even the density of matter in the Universe as a whole.

Let's take a general case first. Suppose that we have a density of n objects per unit volume in a certain region of space, and suppose that each object has a "sphere of influence" with cross-sectional area . In the case of gravitational lensing, this means that any source which lies behind one of these spheres will be lensed by the object.

Suppose that we see a distant object through a distance L of space full of these objects. We can then define a dimensionless quantity called the optical depth, , such that

= n L,

representing the average number of interactions suffered by light reaching us from the distant object. [Convince yourself that defined in this way is indeed the number of interactions and is dimensionless]. For galaxy-mass gravitational lensing, as we have seen, the optical depth is much less than 1, because despite the large distances involved the density of galaxies is low. In fact, the optical depth for galaxy-mass lensing is about 1/500, and we therefore need to examine 500 background objects on average before we find one which is gravitationally lensed.

There are two types of observation we can do.

Compact objects in the universe. For any particular type of gravitational lensing, the optical depth can be determined for a given population of background objects; we simply observe the fraction of background objects which are lensed and hence determine 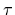. To make further progress we do of course need to know L, which to first order requires that we know the average redshift of the background objects and the distribution of redshifts to do the statistics. We also need to know 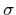, which comes from knowledge of the physics of the lensing object. (For example, if we know about masses of galaxies we can determine the sphere of influence within which lensing will happen). We can then determine the density n of these objects. If we are interested in objects of mass M, we can measure the density of such objects in the Universe provided we make sure that the survey is sensitive to the appropriate image separations, for example about 1 arcsecond for galaxies of mass 10¹² solar masses.
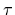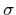Cosmological parameters. The second type of observation is more counterintuitive. In this type of observation we determine as before, and assume that we know the density n of potential lenses and their cross-sectional sphere of influence . We can then calculate the average L to the background objects and compare it to their redshift distributions. This may seem a bizarre thing to do. In practice it is important, because it turns out that the relation of redshift to distance at high redshifts is very sensitive to cosmological parameters, including the matter density of the universe and the "cosmological constant". This gives us a hope of calculating parameters which affect the nature and future of the universe from gravitational lensing studies.

We will discuss these two types of investigation separately. Cosmological theory will be briefly sketched as appropriate, but a more detailed treatment will be given in the final topic of the course.

1. Compact objects in the universe

How much mass does the universe contain, and what form does it take? This is an important question, and it is becoming clear that it has some very strange answers.

From a number of indicators we believe that the total mass density of the universe as a fraction of the critical density is about 0.3. (The critical density is the density required to just slow down and recollapse the universe from its current state of expansion, in the absence of any other complicating factors such as the cosmological constant which will be defined later). This is inferred by studying the dynamics of the largest structures we know about, massive clusters of galaxies, and working out the total mass needed to provide the gravitational force to give the observed motions in these structures.

We also know, as we shall see later, from observations of the cosmic microwave background and reasonably well-understood physics from the early universe, that the density in baryons - "normal" matter such as protons and neutrons - is about 0.04. If the total mass density is 0.3 this already implies that over 80% of the mass of the universe is made up of strange, non-baryonic matter. (The current major candidate is a new weakly-interacting particle known as the axion, but this has not yet been detected).

Of the normal matter, only a fraction is visible to us as luminous matter in stars. This implies that a large amount of dark matter must exist, both in baryonic and non-baryonic forms.

Gravitational lensing is important because any population of compact masses with mass M should be visible by virtue of lensing background objects, on an angular scale (in arcseconds) given by

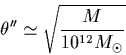Efforts have been made in this direction. In particular, high resolution radio observations can reach the angular scales necessary to detect populations of isotropically distributed compact objects. Recent work by a Jodrell Bank-Caltech collaboration (Wilkinson et al.) indicates that freely-roaming objects in the range of 10-100 million solar masses, if they exist, do not have cosmologically significant mass. In the CLASS survey we observe that all of the gravitational lenses found have luminous lens galaxies, which implies that whole "dark galaxies" (10^11-12 solar masses) do not exist in significant numbers.

2. Cosmological parameters

The matter density as a fraction of critical density is a crucial parameter in cosmology. In the absence of other effects, the universe stops expansion and recollapses, or continues expanding for ever, depending on whether this quantity is greater or less than 1. As already indicated, measurements of 0.3 for this quantity are currently being obtained.

Another effect is, however, likely. Recent evidence from supernovae and studies of the Cosmic Microwave Background radiation taken together suggest the presence of a second quantity, the cosmological constant. This corresponds to an energy with some unusual properties; it remains of constant density as the universe expands, and it acts to accelerate the expansion rather than decelerate it. Its energy as a fraction of the critical energy density is currently thought to be about 0.7. The final part of this course, on cosmology and the cosmic microwave background radiation, treats this problem and the observational situation in more depth.

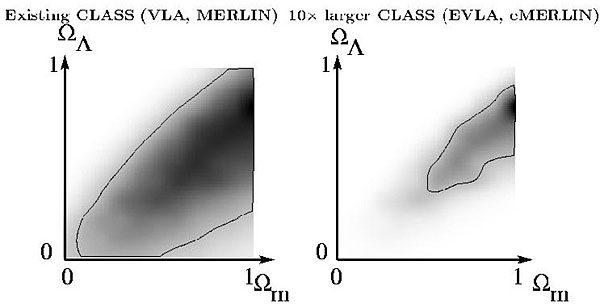
We have already mentioned the effect of these two parameters (the density parameter and the cosmological constant) on lengths within the universe. If we did have a Universe with very low matter density and high (>0.8) values of the cosmological constant, it turns out that this would imply very large values of length for a given interval in redshift in the distant Universe, and hence give rise to a large number of gravitational lenses, more than are observed. Conversely, it currently appears that a universe full of matter (with a matter density greater than or equal to critical) and no cosmological constant would produce too few. Figure 6.1 shows the current information that can be obtained from the CLASS data.

Figure 6.1. Allowed regions of the matter density (on the x-axis) versus energy associated with the cosmological constant (y-axis) parameter space, from current analyses (still under construction) of CLASS gravitational lensing statistics (shown at left). Both quantities are plotted as a fraction of the critical mass density. The region within the contour is consistent with the data and the darkest regions of the grayscale are the most consistent. The point at the bottom right (1,0) is a critical universe with no cosmological constant. More discussion of this diagram and of the spatial structure and history of universes with different parameter values will be given in the last section of the course. The right-hand panel is a simulation of constraints that could be produced by the smaller random errors from a survey such as CLASS, but looking at ten times more objects.

There are some assumptions which have been swept under the carpet in the discussion so far. First, we have assumed that we have a good idea of the galaxy density - in other words, that we know n, and that we know how the galaxy density varies with redshift. Second, we assume that we know all about the background population of quasars that are lensed into our samples such as the CLASS lens sample. Our understanding of both areas is improving, but detailed progress in both is slow and difficult. These assumptions are crucial to using gravitational lenses to make confident statements about the Universe. One could of course take the alternative viewpoint that determination of the cosmological parameters by other means will allow unique insights into galaxy evolution.

In the next section we take a look at other types of gravitational lensing.