1. Introduction
A little bit of history
The path of a ray of light passing through a
gravitational field is bent by the field. This idea is not new; it goes back to
Isaac Newton (1643-1727).
He thought of light as a flow of "corpuscles", or invisible bodies,
which would naturally be affected by a gravitational field. Later in the 18th
century, this concept of light was superseded by the wave theory of light, but
still attempts were made to calculate the exact deflection angle which would be
expected. Soldner in 1801 calculated that this deflection, 
, would be
given for a point mass M by the equation
= 2GM/bc2
where b is the "impact parameter", the
closest distance of the ray to the mass, G is the gravitational constant
(6.67x10-11Nm2s-2) and c is the speed of light
(3x108ms-1). In this equation, the units of are radians;
one radian is equal to about 57 degrees (actually pi radians are exactly equal
to 180 degrees).
Albert
Einstein returned to the problem in 1916. He had developed a theory of
gravity, known as General
Relativity, and one of the results he immediately deduced was that the
classical result for the deflection angle was wrong by a factor of 2 and should
actually be given by
= 4GM/bc2
where is again
measured in radians. In the years after Einstein developed General Relativity,
this was the easiest of its predictions to test observationally. It was done by
Arthur
Eddington in 1919, who observed a star near to the sun during a total solar
eclipse (the eclipse being necessary to avoid the star's light being swamped by
the sun's) and measured that it was displaced in position by a small amount
which was closer to Einstein's prediction of 1.75 arcsecond, about 1/2000 of a
degree, than to the classical prediction.
After its use as a test of General Relativity,
there were relatively few advances in the subject for a long time. Einstein
himself, though, understood that it might be possible for the bending of light
to give very strange effects. In particular, if a background source lay
directly behind a foreground mass, its light could be bent around the mass in
such a way as to spread the light out into a bright ring. The angular radius of
the ring depend on , the
deflection angle, and on the relative distance of the source and the lensing
object as we shall see in the next section. If the background source were
slightly off-centre, more complicated effects could be observed, and in
particular multiple images of the background source could be produced.
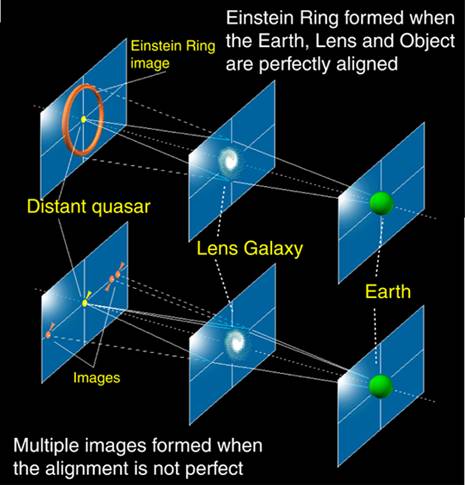
The layout of such a system - a gravitational
lens system - is shown in Figure 1.1. The analogy is with the way a
conventional lens forms images, although the mechanism is different; a
gravitational lens bends the light by the action of gravity, whereas a
conventional lens bends light by refraction at the glass surfaces. The
distortions and multiple images produced by gravitational lenses resemble the
images produced by looking through the curved bottom of a wine bottle.
|
|
|
Figure 1.1. General arrangement of a gravitational lens system. At the top we have the exactly symmetric case, with the source directly behind the gravitational lens. When the symmetry is not exact (bottom) multiple images of the background source are formed. Note in both cases that light is deflected by the gravitational field of the background source. The deflection angles are small, and they depend on the distance the light ray passes from the centre of the deflector and on the mass distribution of the deflector. This will be dealt with in more detail in section 2. |
Discovery of gravitational lenses
Gravitational lens systems are difficult to discover.
A typical gravitational lens system consists of multiple images of a background
quasar at vast distances
(usually several billions of parcsecs), and in principle all one has to do is
to search for this multiple imaging on radio maps or optical plates.
Unfortunately, in a typical star-field a gravitational lens is not easy to
spot. As the name ("QUasi-StellAR object") implies, quasars at
billions of parsecs strongly resemble stars at distances of a few parsecs. For
example, Figure 1.2(a) shows the star-field surrounding the first gravitational
lens system discovered.
|
|
|
|
Figure 1.2. (a) At left: The star-field around the gravitational lens 0957+561, plotted with 8 arcminutes on a side. The gravitational lens is exactly in the centre and consists of two images of a background quasar 6 arcseconds apart (shown boxed). Without prior knowledge, the system would be very difficult to spot! The task would be even more difficult if the separation of the two images were smaller. (b) At right: The radio image, from the FIRST survey (Becker, White & Helfand, Astrophysical Journal, 450, 559). 0957+561 is a radio source, and is visible in the centre of the field. However, the angular resolution in this picture is slightly worse than the optical, and it is not obvious that we are looking at a gravitational lens. Moreover, the quasar has extended radio structure which cannot be seen without a more detailed radio map (Figure 1.4). |
|
The first gravitational lens system was discovered in 1979 by a team led by Dennis Walsh, of the University of Manchester's Jodrell Bank observatory - see the enclosed photocopied article in which Dennis describes the discovery. Throughout the 1960's and early 1970's radio astronomers conducted surveys of the sky (such as the famous 3C survey at Cambridge which led to the discovery of the first quasars) in order to assess what type of objects emitted radio waves. Many of the objects they found were at extremely large distances; when optical plates were searched for coincidences, the radio source often corresponded to a faint galaxy at high redshift.
The work of the Jodrell group particularly focused on finding the sizes of these objects. This could be done using the technique of radio interferometry, in which signals from two telescopes are cobined. See this Layperson's Guide to Radio Astronomy and Interferometry from the MERLIN website at Jodrell Bank for more details.
In the 1960's these experiments used the
To carry on this work, they needed more surveys of fainter quasars. In the early 1970's they were conducting a survey at 966 MHz using the MkIa, and generated a list of radio sources. However, the single-telescope observations on their own did not give accurate positions, and they used the MkIa telescope together with the newer MkII telescope at the other end of the Jodrell site to form an interferometer. This system gave accurate positions which could in principle be used to examine optical plates and decide which of the objects on the optical plates corresponded to the radio object.
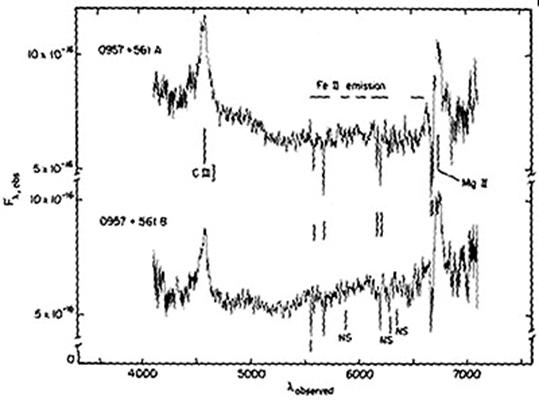
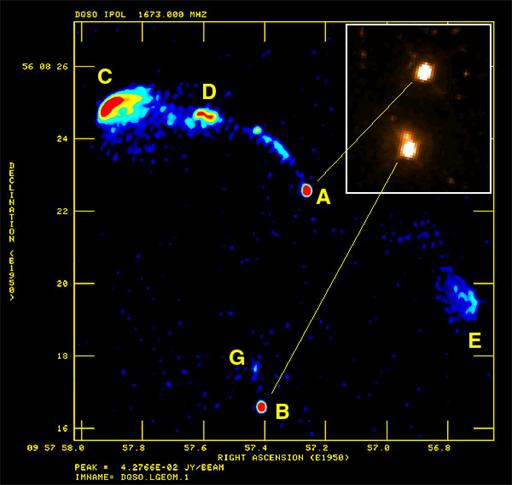
There were some fields, however, for which the interferometer did not give unambiguous results; either the target was very extended and resolved by the interferometer or there was more than one radio source in the telescope beam. Such fields were re-observed with the NRAO 300-foot radio telescope operating at a higher frequency of 5 GHz. [The MkIa did not have a surface accurate enough to allow observations at such short wavelengths, 5GHz is roughly 6cm. Note it is currently being upgraded to allow observations at frequencies as high as 8GHz.] One of the fields with multiple sources in the MkIA beam was close to the galaxy NGC3079. The NRAO 300-foot radio observations found a weak source, 0957+561, below the MkIa survey limit in addition to (and initially, instead of) the strong source NGC3079 with which it had been confused. In fact 0957+561 would never have made it into the survey had it not been for this coincidence. When optical identifications were undertaken, and optical spectroscopy obtained to determine the redshift, the radio source was found to correspond to two optical components, about 6 arcseconds apart, Figure 1.2. It was in principle possible that this represented a chance coincidence of two quasars seen along the same line of sight. However, the optical spectra of the two quasars were virtually identical (Figure 1.3), a fact which argued strongly against the coincidence hypothesis - resulting in the first claim of the observation of a multiple image gravitational lens system. Confirmation in the form of the double nature of the radio source, Figure 1.4, and the presence of a lensing galaxy soon followed, and the observational gravitational lensing era was born.
|
|
|
Figure 1.3. Optical spectra of the two components of 0957+561 seen in Figure 1.2(a) revealing that they are virtually identical (from Wills & Wills 1980). |
|
|
|
Figure 1.4. 0957+561, the first gravitational lens to be discovered. This is a MERLIN radio image. The background source can be seen at the top, and consists of a compact radio core A with ejected radio plasma emerging either side (a jet extending to components C and D on one side and a lobe E on the other). The radio core is imaged into two by the action of the gravitational lens, resulting in the additional component B seen in the image. The inset at top right shows, on a different scale, a Hubble Space Telescope optical image of 0957+561. The two bright components are the double images of the quasar core as seen in Fig. 1.2 and the radio image. The faint blob just above the lower image is emission from the intervening lensing galaxy which can only just be seen in the radio image as component G. |
In the next section we will discuss the geometry of lensing systems in more detail.
Answers to questions
1. The radius of the sun is about 7x108m and its mass is about 2x1030kg. Show that a ray of light which just grazes the Sun and arrives at Earth is deflected by the amount predicted by General Relativity.
Answer to question
The angle is 1.8 arcseconds.
The
mass of the sun is 2x1030kg, so the quantity 4GM/bc2
works out at 8.9x10-6 radians. Converting this to arcseconds
involves multiplying by 57 to get to degrees, and then by 3600 to get to
arcseconds, giving the final result of 1.8 arcseconds.
2. Suppose a ray of light from a distant quasar passes 10kpc from the centre of a galaxy of total mass 1011 that of the sun. (1 kpc = 3x1019m). What is the deflection angle in radians and in arcseconds? What assumptions have you made that may or may not be true?
Answer to question
The
answer is 0.4 arcseconds.
Here the mass of the deflector is 2x1041kg, and
the impactparameter is 3x1020m. Therefore the quantity 4GM/bc2works
out at 1.98x10-6 radians, or about 0.4 arcseconds. Note thatthis
calculation has assumed the galaxy is a point mass
3. In figure 1.2(b) we see the quasar quite clearly but none of the stars. In other words, radio surveys pick out extremely distant objects and filter out stars in our galaxy. Why do you think this is the case?
Answer to question
Stars
and quasars have different distributions of energy over the electromagnetic
spectrum
Stars
radiate as hot bodies at a temperature of a few thousand degrees. Such
radiation is described by a distribution (known as a Planck distribution) which
has a sharp peak in wavelength and tails off sharply either side. The position
of this peak depends on the temperature, and for stars it falls in the optical.
Since radio waves are at very different wavelength, the radio emission from
most stars is negligible. The radio emission from quasars, however, is produced
by a different process (synchrotron radiation) which has a very different
dependence on wavelength and does give significant emission at radio
wavelengths.