We can simplify this classification of solutions (excluding the matter-free
ones) by choosing parameters
other than ![]() and k to classify the shape.
Every universe contains
either a turning point where H =0, or a point of inflection where
the acceleration is zero. Classify the former by the ratio
xturn of
and k to classify the shape.
Every universe contains
either a turning point where H =0, or a point of inflection where
the acceleration is zero. Classify the former by the ratio
xturn of ![]() -to-matter density at the turning point
(where
-to-matter density at the turning point
(where
![]() =
= ![]() by definition),
and the latter by
by definition),
and the latter by
![]() , the density parameter at inflection,
(where
xi = 1/2 by definition).
As the following table shows,
xturn varies smoothly
from infinity to minus infinity through all the solutions with turning points:
, the density parameter at inflection,
(where
xi = 1/2 by definition).
As the following table shows,
xturn varies smoothly
from infinity to minus infinity through all the solutions with turning points:
| k | rturn | xturn | Type | |
| positive, |
+1 |
(3/ |
3/2(3/ |
Bounce |
| 1/2 | +1 | 2 | 2 | Bounce |
| 27/32 | +1 | 4/3 | 1 | Bounce |
| 1 | +1 | 1 | 1/2 | Loiter |
| 0 | +1 | 2/3 | 0 | Bang-crunch |
| -4 | +1 | 1/2 | -1/4 | Bang-crunch |
| +1 |
(- 2/ |
-1 | Bang-crunch | |
| negative | 0 |
(- 2/ |
-1 | Bang-crunch |
| -1 |
(- 2/ |
-1 | Bang-crunch | |
| -5 | -1 | 1 | -5/2 | Bang-crunch |
| -1 | -1 | 2 | -4 | Bang-crunch |
| negative,
| |
-1 |
(- 3/ |
-6(- 3/ |
Bang-crunch |
Although xturn is continuous, the bounce universes effectively form a separate solution family.
Similarly,
![]() varies from zero to positive infinity
through all the continuous expansion solutions (in this case we always have
ri =
varies from zero to positive infinity
through all the continuous expansion solutions (in this case we always have
ri = ![]() ):
):
| k | ri |
|
|
| positive, |
-1 |
|
|
| 1/8 | -1 | 2 | 1/3 |
| 1 | -1 | 1 | 1/2 |
| 8 | -1 | 1/2 | 2/3 |
| -1 | 1 | ||
| positive | 0 |
|
1 |
| +1 | 1 | ||
| 8 | +1 | 1/2 | 2 |
| 1 | +1 | 1 | + |
The three families intersect at the loitering solution,
where ![]() just reaches infinity, so
ri = rturn = 1 at the Einstein point.
Also the bang-crunch and continously expansion families meet at
the k = - 1 cycloid
solution, which is equivalent to a bang-crunch solution with
xturn = -
just reaches infinity, so
ri = rturn = 1 at the Einstein point.
Also the bang-crunch and continously expansion families meet at
the k = - 1 cycloid
solution, which is equivalent to a bang-crunch solution with
xturn = - ![]() , and also to a continuous expansion
solution with
, and also to a continuous expansion
solution with
![]() = 0. The final limit,
with
xturn = +
= 0. The final limit,
with
xturn = + ![]() is equivalent to the
de Sitter solution.
is equivalent to the
de Sitter solution.
In terms of ![]() and k, the new parameters are given
by
and k, the new parameters are given
by
|
xturn = |
(17) |
The turnaround radius rturn is given by positive real roots of the cubic equation:
|
2 - 3kr + |
(18) |
We can convert from these new parameters back to ![]() ,
k using
,
k using
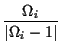 |
(19) |
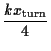 |
(20) |